Ряд Фурье для этой функции имеет следующий вид:
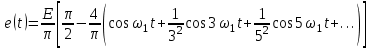(2.8)



Последовательность униполярных прямоугольных импульсов (рисунок 2.7)
Применяя формулы

,

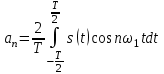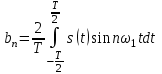
находим среднее значение (постоянную составляющую)


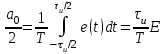
(2.9)
и коэффициент n-й гармоники

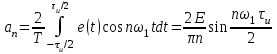
Так как функция четная, 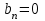и 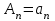. Таким образом,
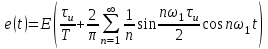(2.10)
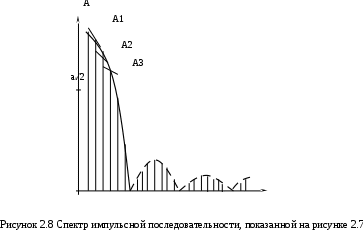
Величина 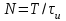называется скважностью импульсной последовательности. При больших значениях N спектр сигнала содержит очень большое число медленно убывающих по амплитуде гармоник (рисунок, 2.8). Расстояние между спектральными линиями очень мало, а амплитуды соседних гармоник близки по величине. Это в данном случае удобно представить в несколько измененном виде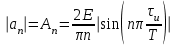

При малых значениях п можно считать
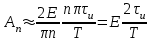(2.11)
Постоянная составляющая, равная 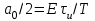, вдвое меньше амплитуды первой гармоники. При построении спектра коэффициентов 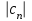величина 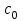приближенно равнялась бы .

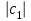Краткая характеристика исследуемых цепей и сигналов

---

В работе используются блоки ИСТОЧНИКИ СИГНАЛОВ, сумматор () и КОДЕР универсального лабораторного стенда. Сменные блоки в этой работе не используются.

В качестве простейших гармонических используются сигналы с частотами 1 и 2 кГц (два левых верхних гнезда стенда) и встроенный диапазонный генератор типа Г3-111.

Источники сигналов сложной формы, состоящих из двух гармоник (2 и 4 кГц, 2 и 6 кГц) расположены ниже – это гнёзда S₁, S₂ и S₃. Два последних сигнала отличаются фазой третьего гармоники. Все сигналы стенда (кроме встроенного ЗГ), жёстко синхронизованы, т. к. получены от общего кварцевого генератора путём деления частоты. Это упрощает задачу получения неподвижного изображения на осциллографе.

Источником импульсной последовательности является блок КОДЕР, позволяющий формировать произвольную пятисимвольную последовательность, повторяющуюся с периодом 17T, где T=512мкс – длительность одного символа.

В качестве измерительных приборов используются: встроенный вольтметр типа В7-38, двулучевой осциллограф и ПК в режиме анализа спектра.
Лабораторное задание
1. Наблюдайте осциллограммы и измерьте спектры простых гармонических сигналов.

2. Исследуйте форму и спектры сложных гармонических сигналов.

3. Исследуйте связь формы и спектра периодических последовательностей прямоугольных импульсов

---

Порядок выполнения работы

Моногармонический сигнал
2.1 Подключить осциллограф к гнезду “1 кГц” стенда. Ручку регулятора выхода сигнала поставить в среднее положение. Зафиксировать в отчёте осциллограмму сигнала и измерить его период по делениям на экране с учётом цены деления (мкс/дел) переключателя развёртки.

2.2 Соединить гнездо “1кГц” с входом ПК, расположенным в нижней части стенда, правее сменного блока. Для этого надо применять специальный кабель (входит в комплект стенда) с разъёмом типа “колокольчик”. Процедура анализа спектра с помощью ПК описана в Приложении.

Зафиксируйте в отчёте спектр сигнала, указав там условия эксперимента, амплитуды и точные значения частот спектральных линий (в обозначениях на стенде даны округлённые значения частот).
Сложные гармонические сигналы
2.3 Подавая сигнал от гнезда S₁ блока ИСТОЧНИКИ СИГНАЛОВ на вход осциллографа, зафиксировать форму S₁(t) исследуемого сигнала и его период, а затем – на вход ПК, фиксируя амплитуды и частоты спектра сигнала.

2.4 Повторить п. 2.3 для сигналов S₂ и S₃.

2.5 Подать сигнал S₂ на один из входов сумматора () стенда; на второй его вход – сигнал от гнезда “1кГц”. Наблюдая осциллограмму сигнала на выходе сумматора, плавно увеличивать уровень сигнала “1кГц”, добиваясь заметного изменения формы суммарного сигнала. Для полученного суммарного сигнала зафиксировать осциллограмму (с указанием периода) и его спектр.
Бигармонический сигнал

2.6 Бигармонический сигнал состоит из двух гармонических сигналов, частоты которых не обязательно находятся в кратных соотношениях. Такими сигналами в данном случае будут: вышеупомянутый “1кГц” из блока ИСТОЧНИКИ СИГНАЛОВ и 1,2 кГц от встроенного ЗГ типа Г3-111. Оба этих сигнала надо подать на входы сумматора, выставив напряжение каждого из них по 0,5 В. Для этого использовать встроенный вольтметр В7-38. Подать суммарный сигнал сначала на осциллограф, зафиксировать его форму с указанием периода суммарного сигнала, а затем на вход ПК, зафиксировав его спектр.
Периодическая последовательность прямоугольных импульсов
2.7 Периодическая последовательность прямоугольных импульсов формируется в блоке КОДЕР. “Нули” и ”единицы” цифрового сигнала задаются пятью тумблерами (b

---

₁b₅) со светодиодной индикацией с надписью ПЕРЕДАНО.

2.8 Соединить выходные гнёзда КОДЕРА с входом осциллографа и ПК.

2.9 Набрать в КОДЕРЕ комбинацию 10000 (длительность импульса Т=512 мкс, а период – 17Т). Зафиксировать в отчёте форму и спектр сигнала.

2.10 Повторить п.2.9, набрав комбинацию 11000 (длительность импульса 2Т=1024мкс, период – 17Т).

2.11 Повторить п. 2.9 для комбинации 11110 (длительность импульса 4Т=2048мкс, период – 17Т).

Содержание отчета

1. Название сигнала, осциллограмма с указанием периода сигнала, спектрограмма с указанием амплитуд в делениях и частот составляющих в Герцах;

2. Выводы.

Контрольные вопросы:

1. Какова математическая связь формы периодического сигнала и его спектра?

2. То же для непериодических (однократных) сигналов.

3. Что такое прямое и обратное преобразование Фурье?

4. В каких случаях можно применить ряд Фурье для спектрального анализа?

5. Меняется ли спектр сложного сигнала при прохождении его через линейную цепь (например, ФНЧ)?

6. Меняется ли форма моногармонического сигнала при прохождении его через ФВЧ?

7. Меняется ли форма сложного сигнала при прохождении его через линейный четырёхполюсник?

8. Что такое спектральная плотность амплитуд?

9. Влияет ли фазовый спектр сигнала на его форму?

10. От каких параметров сигнала зависит спектр периодической последовательности прямоугольных импульсов?

11. Как связана длительность сигнала и ширина его спектра?

ЛАБОРАТОРНАЯ РАБОТА №3
"ПРЕОБРАЗОВАНИЕ ФОРМЫ И СПЕКТРА СИГНАЛОВ

БЕЗИНЕРЦИОННЫМ НЕЛИНЕЙНЫМ ЭЛЕМЕНТОМ "
Цель работы: изучение формы и спектра сигналов на выходе резистивной цепи, содержащей нелинейный безинерционный элемент при моно- и бигармоническом воздействии.
Краткие сведения из теории

Исследование нелинейной цепи задача весьма сложная в том отношении, что при математическом описании функционирования такой системы мы сталкиваемся с проблемой решения нелинейных дифференциальных уравнений. Известно, что здесь не применимы большинство приёмов и методов, которые позволяют относительно легко решать линейные дифференциальные уравнения с постоянными коэффициентами. Тем не менее, в ряде случаев исследования нелинейных систем удаётся довести до конца простыми способами. Для этого достаточно потребовать, чтобы нелинейная зависимость вида:

---

U_вых(t)=f(U_вх,t) (3.1)
Не содержала явно времени. Физически такое требование означает безинерционность нелинейного элемента, т.е. мгновенное установление выходной реакции вслед за изменением внешнего входного воздействия. Безинерционных нелинейных элементов, строго говоря, не существуют. Однако эта идеализация достаточно точна, если характерное время изменения входного сигнала значительно превышает время установления процесса внутри самого нелинейного элемента.

В радиотехнике нелинейные элементы – это чаще всего полупроводниковые приборы – диоды, биполярные и полевые транзисторы. Современные полупроводниковые приборы достаточно совершенны по своим частотным свойствам. Поэтому предположение о безинерционном характере внутренних процессов в нелинейных радиотехнических элементах часто бывает оправданным.

Функциональную зависимость, рассмотренную ранее можно представить как простейшую математическую модель нелинейного элемента. Особенность её состоит в том, что здесь не фигурируют процессы, происходящие внутри элемента. Принято говорить, что имеют дело с внешней характеристикой системы.

Можно выделить класс элементов с однозначными вольтамперными характеристиками и класс элементов, характеристики которых содержат участки многозначности.

Классификация цепей

Радиотехнические цепи и элементы, используемые для осуществления преобразовании сигналов и колебаний (преобразование исходного сообщения в электрический сигнал и кодирование, генерация высокочастотных колебаний, управление колебаниями (модуляция), выделение сообщения из высокочастотного колебания (детектирование о декодирование)) можно разбить на следующие классы:

- линейные цепи с постоянными параметрами,

- линейные цепи с переменными параметрами,

- нелинейные цепи.

В реальных радиоустройствах четкое выделение линейных и нелинейных цепей и элементов не всегда возможно. Отнесение одних и тех же элементов к линейным или нелинейным часто зависит от уровня воздействующих на них сигналов.

Радиотехническое устройство независимо от своего назначения и уровня сложности представляет собой систему, т.е. совокупность физических объектов, между которыми существуют определенные взаимодействия.

Рисунок 3.1 - Система (системный оператор)
На вход подается исходный сигнал, а с выхода снимается преобразованный сигнал.

---

Смотрите также файлы

• Задания для повторения курса алгебры 7 класса.ppt

• Творческий проект.docx

• йел педагог.docx

• Илясова Елизавета, группа 4202.docx

• Конспект 1 Конспект 2 Задание 1 Задание 2 Задание 3 1 практическое задание 2 практическое задание.doc