U_m2




Рисунок 3.7 Преобразование на кусочно-параболическом участке ВАХ

Бигармоническое воздействие
3.9 Бигармоническое воздействие u_ЗИ = Е_СМ + U_1mcos2f₁t+ U_2mcos2f₂t

В качестве второго гармонического сигнала с частотой f₂=1,2кГц используется звуковой генератор Г3-111 в блоке ИСТОЧНИКИ. На один из входов сумматора подать прежний сигнал f₁=1кГц, на любой другой - f₂=1,2кГц.
Преобразование на квадратичном участке ВАХ
3.10. Установить смещение Е_СМ=Е_СМ1=u₀/2 (рабочая точка на середине квадратичного участка ВАХ).

3.11 Установить одинаковые амплитуды сигналов от разных источников на обоих входах сумматора U_1m=U_2m=u₀/4, при этом суммарный сигнал ("биения") не выйдет за пределы квадратичного участка.

3.12 Повторить п.3.5 для новых параметров сигналов, заполнив соответствующую таблицу.

3.13 Повторить п. 3.5., предварительно уменьшив вдвое амплитуду одного из сигналов.

Преобразование на кусочно-параболическом участке ВАХ
3.14 Установить Е_СМ=Е_СМ2=u₀

3.15 Установить амплитуды сигналов U_1m=U_2m= u₀/2

3.16 Повторить п. 3.5 для новых параметров сигналов.

---

Содержание отчета
1. Принципиальная схема исследования.

2. Сток-затворная характеристика исследованной нелинейной цепи.

3. Аппроксимация ВАХ для работы на квадратичном (параболическом), кусочно-линейном и кусочно-параболическом участках.

4. Теоретический расчет спектра для данных, использованных в эксперименте (по указанию преподавателя).

5. Осциллограммы и спектры исследованных процессов.
Контрольные вопросы:
1. Каковы характерные особенности спектров тока, протекающего через нелинейный безинерционный элемент, при моно- и бигармоническом воздействиях?

2. Что называется порядком комбинационного колебания? Поясните примером.

3. Какова связь между наивысшим порядком комбинационного колебания и степенью полинома, аппроксимирующего характеристику нелинейного элемента?

4. Перечислите наиболее часто применяемые методы спектрального анализа колебаний на выходе без инерционных нелинейных преобразователей. Укажите, при каких видах аппроксимации целесообразно применять каждый из них.

5. Что называется углом отсечки, как определить его по осциллограмме сигнала и как выразить аналитически?

6. Характеристика нелинейного элемента аппроксимирована ломаной линией. Входное воздействие представляет собой сигнал вида u=Е_СМ+U_mcos2t. Пользуясь системой трех координатных плоскостей, покажите, как следует выбрать Е_СМ и U_m, чтобы:

а) ток по форме повторял форму входного сигнала;

б) ток принял форму косинусоидальных импульсов с углом отсечки 90⁰.

7. Поясните, как работает преобразователь, принципиальная схема которого приведена на рисунке 3.4.

8. Как практически изменить положение рабочей точки на сток-затворной характеристике полевого транзистора?

9. Перечислите все составляющие спектра тока, если на вход нелинейного элемента с параболической (квадратичной) ВАХ подать гармонические сигналы с частотами 5 и 6 КГц.

10. То же для случая аппроксимации ВАХ степенным полиномом третьей степени.

11. Как изменится спектральный состав тока, если амплитуду входного напряжения уменьшить в 10 раз?

ЛАБОРАТОРНАЯ РАБОТА №4
"ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ ВО ВРЕМЕНИ

---

(ТЕОРЕМА КОТЕЛЬНИКОВА)"
Цель работы: исследование процессов дискретизации и восстановления непрерывных сигналов.
Краткие сведения из теории
Некоторые из непрерывных сигналов имеют ограниченный спектр. Для таких сигналов справедлива теорема Котельникова: непрерывный сигнал с ограниченным спектром полностью определяется своими значениями в дискретные моменты времени, отстоящими друг от друга на время 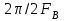, где F_в – верхняя граничная частота спектра этого сигнала, t – называется интервалом дискретизации по времени.



Рисунок 4.1 Дискретизация сигнала

На основе теоремы Котельникова непрерывный сигнал с ограниченным спектром может быть передан путем передачи его мгновенных значений, отсчитываемых в дискретные моменты времени – дискретных отсчетов, т. е. фактически задача сводится к передаче последовательности чисел.

Эта теорема указывает следующие условия:

а) спектр передаваемого сигнала должен быть ограничен верхней граничной частотой F_в;

б) частота следствия импульсов – отсчетов или частота дискретизации F_g.

F_g 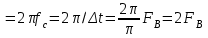(4.1)
Если истинное мгновенное значение сигнала U(t), подлежащее передаче попадает между разрешенными значениями, то амплитуда передаваемого импульса принимается равной разрешенному значению, являющемуся ближайшим, к истинному. Такое преобразование называется квантованием, совокупность разрешенных значений амплитуд передаваемых импульсов – шкалой квантования, а интервал между соседними разрешенными значениями – шагом квантования.

Квантование приводит к ошибке квантования (шум квантования) E(t)=Z(t) – v(t). Квантование при передаче сигналов, во–первых позволяет применить импульсно – кодовую модуляцию и, следовательно, использовать все преимущества, обеспечиваемые ею, во – вторых представляет собой мощное средство борьбы со случайными помехами.
Применяемая аппаратура



Исследуемое устройство (рисунок 4.2) размещено на сменном блоке ТЕОРЕМА КОТЕЛЬНИКОВА и представляет собой дискретизатор (обозначенный на макете как перемножитель сигналов) и набор из трех фильтров - восстановителей с разными частотами среза.

---

Источники исследуемых сигналов - S₁, S₂ и S₃ находятся в блоке ИСТОЧНИКИ СИГНАЛОВ, а сами сигналы представляют собой суммы гармоник с частотами 2, 4 и 6кГц. (При необходимости исследуемый сигнал может быть усложнен добавлением еще одного гармонического сигнала с частотой 1кГц с помощью сумматора стенда).

Д





искретизатор, формирующий отсчеты s(kt) непрерывного сигнала s(t), выполняет функцию перемножителя этого сигнала на короткие импульсы напряжения дискретизации (u_дискр). В данном случае дискретизатор выполнен по схеме аналогового коммутатора, пропускающего входной сигнал s(t) на выход в течение короткого времени существования импульсов дискретизации. Временной интервал между соседними отсчетами дискретизированного сигнала s(kt) зависит от выбора частоты дискретизации f_д:
t=1/ f_д. (4.2)
Эта частота может изменяться дискретно при нажатии кнопки f_д, при этом выбранное значение этой частоты индицируется светодиодом (f_д=3,6,12,16,24 и 48 кГц). Все упомянутые выше частоты (частоты дискретизации и частоты гармоник исследуемых сигналов) жестко синхронизированы, что упрощает наблюдение процессов на осциллографе.

В качестве фильтров - восстановителей используются три активных ФНЧ четвертого порядка с частотами среза 3, 6 и 12 кГц. Для снятия импульсных характеристик фильтров используется генератор коротких импульсов " - функций" (гнезда (t) в блоке ИСТОЧНИКИ СИГНАЛОВ).




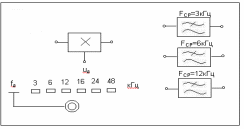
Р


исунок 4.2 Сменный блок ТЕОРЕМА КОТЕЛЬНИКОВА
В соответствии с теоремой Котельникова отсчеты, следующие через интервалы времени t=1/2F_В, где F_В - верхняя частота сигнала, могут быть преобразованы в исходный сигнал после прохождения через идеальный ФНЧ с частотой среза F_СР = F_В. В работе используются реальные ФНЧ с достаточно крутыми спадами АЧХ после частоты среза. Поэтому на практике выбирают t несколько меньше (а иногда и в несколько раз меньше), чем требуется в теореме Котельникова с тем, чтобы реальный ФНЧ с АЧХ трапециевидной формы позволял выделить спектр исходного сигнала из спектра дискретизированного сигнала, что гарантирует отсутствие искажений при обратном преобразовании (восстановлении) сигнала.

---

В качестве измерительных приборов используются двулучевой осциллограф и ПК, работающий в режиме анализатора спектра.
Лабораторное задание
1. Произвести дискретизацию одного из сложных сигналов (S₁, S₂ или S₃).

2. Исследовать спектры исходного и дискретизированного сигналов.

3. Исследовать частотные и импульсные характеристики фильтров – восстановителей.

4. Исследовать процесс восстановления дискретизированных сигналов.
Порядок выполнения работы
Дискретизация сигнала
4.1 Выбрать один из трех сигналов (например, S₁) в блоке ИСТОЧНИКИ СИГНАЛОВ и подать его на вход "А" ПК, работающего в режиме спектроанализатора. (Входы ПК находятся в нижней части стенда справа).

4.2 С помощью спектроанализатора (ПК) получить спектр сигнала и определить его верхнюю частоту (F_В).

4.3 Учитывая, что значения частот дискретизации (f_д), указанных на сменном блоке, являются ориентировочными, провести спектральный анализ сигналов U_Д (гнездо под перемножителем). Определив частоты первых гармоник этих сигналов при установке f_Д = 3, 6, 12 и 16 кГц, внести уточненные значения в таблицу 4.1.

Для частот более 24 и 48 кГц спектральный анализ в данной работе невозможен (так как F_max = 24 кГц), поэтому их следует умножить на тот же коэффициент, который связывает указанные на блоке и уточненные значения частот дискретизации. (Этот коэффициент (≈1,15) может быть уточнен по первым четырем значениям f_Д).
Таблица 4.1 – Уточненные частоты дискретизации (f_Д)

Обозначение на блоке	кГц	3	6	12	16	24	48
Измеренное (рассчитанное)	кГц

4.4 Рассчитать требуемую частоту дискретизации f_д и установить ее на макете кнопкой " f_д ".

4.5 Соединить входы двулучевого осциллографа со входом и выходом дискретизатора, установить режим внешней синхронизации осциллографа (от гнезда С2 блока ИСТОЧНИКИ). Вход спектроанализатора подключить к выходу дискретизатора.

---

Смотрите также файлы

• Задания для повторения курса алгебры 7 класса.ppt

• Творческий проект.docx

• йел педагог.docx

• Илясова Елизавета, группа 4202.docx

• Конспект 1 Конспект 2 Задание 1 Задание 2 Задание 3 1 практическое задание 2 практическое задание.doc