4.6 Зафиксировать в отчете временные диаграммы в следующем порядке (с сохранением масштаба по оси времени)

- исследуемый сигнал s(t);

- напряжение дискретизации (гнездо нижнего входа перемножителя);

- выходной дискретизированный сигнал s(kt).

С экрана монитора ПК зарисовать спектры перечисленных выше сигналов.

4.7 Переключая кнопкой частоту дискретизации f_д на 1-2 шага выше и ниже выбранного значения f_д, наблюдать изменения в осциллограммах и спектрах на выходе дискретизатора. Наиболее характерные случаи зафиксировать в отчете.
Исследование фильтров
С целью выбора наилучшего из трех ФНЧ в качестве фильтра - восстановителя необходимо определить частоту среза каждого из них по АЧХ либо по импульсной характеристике g(t). Кроме того, АЧХ фильтров необходима для последующей коррекции f_д, а импульсная реакция g(t) нужна для объяснения процесса восстановления сигнала.

4.8 Снятие АЧХ фильтра проводиться путем подачи на его вход гармонического сигнала с напряжением 1В и с частотой 1кГц от встроенного генератора Г3-111 в блоке ИСТОЧНИКИ СИГНАЛОВ. К выходу фильтра подключить встроенный цифровой вольтметр переменного напряжения типа В7-38. Плавно увеличивая частоту генератора, снять частотную характеристику U_ВЫХ=(f) с шагом 1-2кГц так, чтобы зафиксировать частоту среза F_С, на которой U_ВЫХ окажется в2 раз меньше, чем на частоте 1кГц, а также частоты, на которых U_ВЫХ уменьшится до 0,1 и 0,05 от U_ВЫХ(1кГц). Построить на одном графике АЧХ трех фильтров и отметить на них уточненные значения частот среза F_С. Выбрать лучший фильтр - восстановитель для исследуемого сигнала.

4.9 Снятие импульсной реакции ФНЧ производится путем подачи на вход фильтра коротких импульсов (от гнезда "(t)" блока "ИСТОЧНИКИ"). Осциллограмма выходного сигнала будет соответствовать импульсной реакции фильтра g(t). Зарисовать осциллограммы g(t) для трех фильтров, фиксируя на них значения "нулей" (рисунок 4.3.) по шкале на экране осциллографа с учетом масштаба развертки (мкс/дел). Определив t^ для каждого ФНЧ, находим частоты среза по формуле:
F_С =1/(2 t ^). (4.3)
4.10 По пунктам (4.8) или (4.9) выбрать фильтр, наиболее пригодный для восстановления дискретизированного сигнала.







Р

---

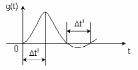
исунок 4.3 Импульсная реакция ФНЧ
Восстановление дискретизированного сигнала
4.11 Сопоставляя спектры, снятые по пункту 4.6 с частотной характеристикой выбранного фильтра - восстановителя, скорректировать частоту дискретизации, увеличив ее на 1 - 2 шага от расчетного значения с тем, чтобы спектр исходного сигнала s(t) можно было выделить из спектра дискретизированного сигнала с помощью выбранного реального ФНЧ.

4.12 Соединить выход дискретизатора с входом выбранного ФНЧ, установить на макете уточненное в пункте 4.11 значение f_д^. Подключив один из входов осциллографа к входу дискретизатора, а второй - к выходу ФНЧ, зафиксировать в отчете осциллограммы исходного и восстановленного сигнала.

4.13 Изменяя частоту дискретизации на 1 - 2 шага от скорректированного значения f_д, зафиксировать наиболее характерные осциллограммы восстановленных сигналов. В отчете привести заключение о том, допустимо ли изменять интервал между отсчетами дискретизированного сигнала (t).

4.14 Установив прежнее значение f_д^, заменить выбранный ФНЧ на другой, а затем и на третий фильтр, фиксируя в отчете осциллограммы восстановленных сигналов с указанием F_С ФНЧ.

4.15 Соедините вход дискретизатора с источником периодической последовательности прямоугольных импульсов, в качестве которого используется КОДЕР. Установите тумблерами КОДЕРА любую комбинацию из одной единицы и четырех нулей. При этом на выходе КОДЕРА формируются прямоугольные импульсы длительностью 512мкс с периодом 8704 мкс. Проведя анализ спектра этого сигнала, выберите f_д и фильтр восстановитель. Зафиксируйте осциллограммы и спектры входного, дискретизированного и восстановленного сигналов.
Содержание отчета
1. Функциональная схема установки.

2. Осциллограммы, спектры и характеристики фильтров по всем пунктам задания.

3. Выводы.
Контрольные вопросы:
1. Каков практический смысл в дискретизации аналоговых сигналов?

2. Сформулируйте теорему Котельникова.

3. При каких условиях теорема Котельникова гарантирует двойное преобразование сигналов (дискретизация и восстановление) без искажений?

4. Могут ли быть дискретизированы и затем восстановлены импульсы прямоугольной формы?

5. Каков алгоритм восстановления дискретизированного сигнала?

---

6. Какова роль ряда Котельникова в объяснении процесса восстановления сигнала?

7. Что такое базисная функция?

8. Какую функцию выполняет ФНЧ?

9. С какой целью в работе исследовались спектры исходного и дискретизированного сигналов?

10. Можно ли произвольно увеличивать или уменьшать t между отсчетами? К чему это может привести?

11. В чем отличие идеального и реального ФНЧ?

12. С чем связана необходимость корректировать значение частоты дискретизации?

13. Как Вы представляете себе процесс дискретизации аналогового сигнала? Какие функциональные узлы для этого необходимы?

14. Все ли аналоговые сигналы могут быть:

- дискретизированы во времени;

- восстановлены после дискретизации.

15. Назовите причины, вызывающие искажения при восстановлении дискретизированных сигналов.
ЛАБОРАТОРНАЯ РАБОТА №5
АМПЛИТУДНАЯ МОДУЛЯЦИЯ
Цель работы: исследование процесса амплитудной модуляции, получение статической модуляционной характеристики и выбор оптимального режима работы модулятора.
Краткие сведения из теории
Для сигналов с аналоговыми видами модуляции удобно использовать квазигармоническое представление:
,
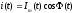где 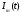- огибающая процесса, 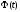- полная фаза .

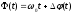Первое слагаемое здесь - текущая фаза, второе - девиация (отклонение) фазы. Учитывая, что 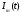и 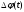- суть медленно меняющиеся функции времени, за один период колебания с несущей частотой ₀, модулированный сигнал по форме представляет собой синусоиду. Этим и объясняется название "квазигармоническое", то есть почти синусоидальной формы.

Амплитудную модуляцию можно определить как вид модуляции, при котором девиация амплитуды пропорциональна информационному сигналу 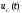, а девиация фазы 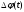вырождается в начальную фазу .
,

---

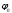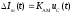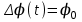
(5.1)

где К_АМ - коэффициент пропорциональности, характеризующий работу модулятора. Физический смысл этого коэффициента будет показан ниже.

Огибающая процесса может быть представлена как сумма постоянной составляющей (амплитуды несущего колебания) и девиации амплитуды: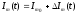
(5.2)
Общая запись амплитудно-модулированного сигнала (АМ) имеет вид:
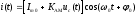(5.3)
Для частного случая, тональной АМ:
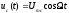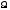; (  ₀)

.
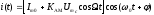Величина 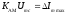; вынося 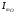за скобку, получим: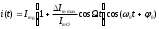


Обозначим 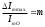(глубина модуляции).

Окончательно для тональной модуляции:
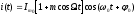(5.4)

Для модуляции сложным сигналом 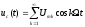, а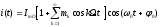

здесь 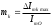- частичная (парциальная) глубина модуляции; .

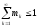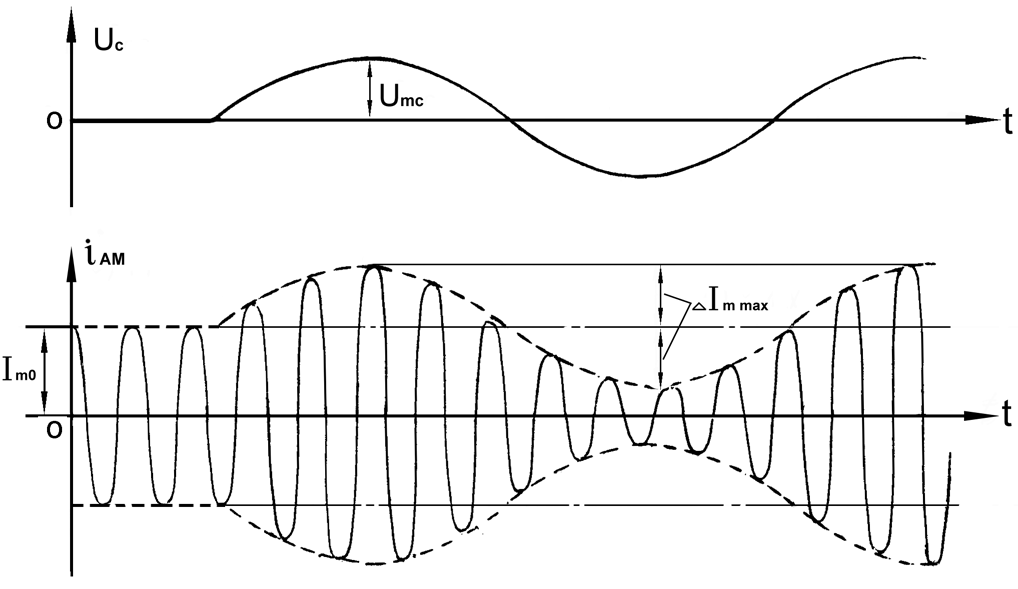
Временные диаграммы информационного сигнала 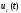и сигнала АМ представлены на рисунок 6.1.

Для получения спектра тонального АМ сигнала раскроем скобки выражения (6.4)
.
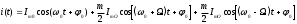С
пектрограммы исходного (информационного) сигнала и АМ сигнала показаны на рисунке 5.2.
Рисунок 5.1 Временные диаграммы тонального АМ сигнала
Спектр тонального АМ сигнала состоит из колебания несущей частоты и двух боковых, которые являются комбинационными частотами.

Итак, новыми колебаниями, возникающими в амплитудном модуляторе, являются комбинационные колебания второго порядка 

---

₀  . Следовательно, наилучшей формой ВАХ нелинейного элемента в амплитудном модуляторе является квадратичная парабола: 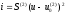при 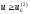. Если на вход нелинейного элемента подать бигармонический сигнал 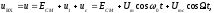в спектре тока , кроме гармоник входных сигналов, образуются комбинационные колебания второго порядка :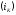



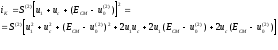
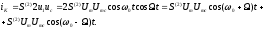(5.5)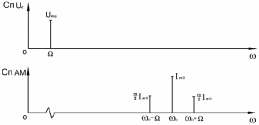

Рисунок 5.2 Спектр тонального АМ сигнала
Весь спектр тока показан на рисунке 6.3 Для выделения из спектра тока полезных компонентов сигнала (₀, ₀) необходимо применить полосовой фильтр с центральной частотой ₀ и полосой пропускания не уже 2.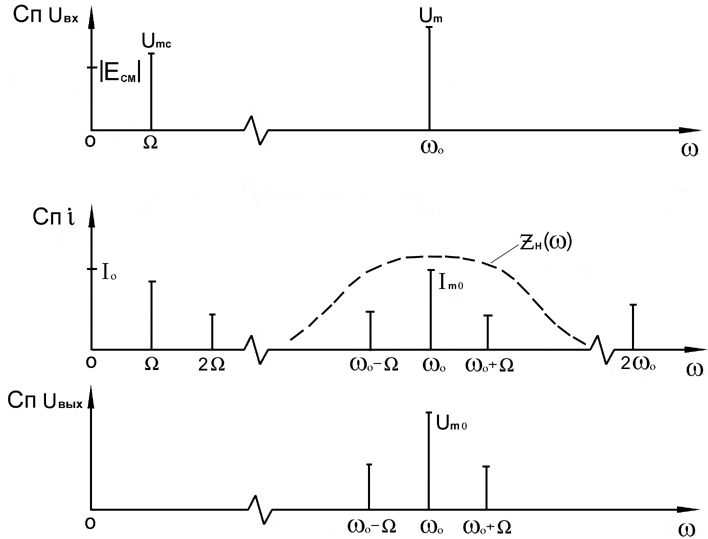





Рисунок 5.3 Спектры амплитудного модулятора

В простейшем варианте таким полосовым фильтром может быть параллельный контур с невысокой добротностью. (При высокой добротности контура в спектре выходного напряжения будут подавлены боковые частоты).

Для нахождения оптимального режима работы модулятора следует получить (расчетным или экспериментальным путем) статическую модуляционную характеристику (СМХ) 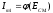при 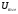= const. Эта характеристика показывает возможности модулятора в изменении амплитуды сигнала.

Строятся несколько таких характеристик для разных амплитуд колебаний несущей частоты ( 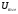), и из них выбирается та, которая имеет наибольший по протяженности линейный участок. Требование линейности СМХ вытекает из определения АМ. Тангенс угла наклона линейного участка СМХ (угла  на рисунке 5.4) является коэффициентом пропорциональности К_АМ. С помощью СМХ можно определить оптимальный режим амплитудного модулятора и его параметры:

- выбор оптимальной амплитуды сигнала несущей частоты

---

Смотрите также файлы

• Задания для повторения курса алгебры 7 класса.ppt

• Творческий проект.docx

• йел педагог.docx

• Илясова Елизавета, группа 4202.docx

• Конспект 1 Конспект 2 Задание 1 Задание 2 Задание 3 1 практическое задание 2 практическое задание.doc