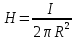ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 124
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(00)
Рисунок 1.10 – понятие фазы колебаний
Приняв за начало отсчета момент начала колебаний одной из синусоидальных величин, изменяющихся с одной частотой (например напряжения) можно определить время (угол) отставания или опережения по фазе другой или других величин (например тока).
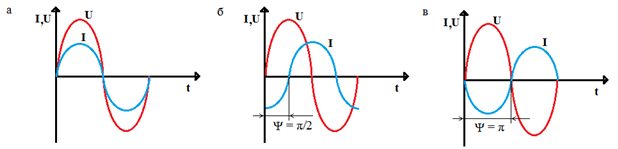
Рисунок 1.11 – Сдвиг фазы колебаний двух величин (а) – величины имеют одинаковую фазу (находятся в фазе), (б) – одна величина (ток) отстает по фазе на 900 (сдвиг по фазе), сдвиг по фазе составляет 1800 (величины находятся в противофазе)
1.11 Векторные диаграммы
Оперировать гармоническими величинами, представленными в виде синусоидальных функций, оценивая их взаимодействия, практически неудобно. Поэтому для анализа переменных электрических величин используют векторные диаграммы.
Гармонические функции при этом изображают векторами, вращающимися относительно начала прямоугольной системы координат, против часовой стрелки с угловой скоростью ω. При этом всегда можно осуществить переход от синусоиды к вектору и наоборот (рис. 1.12).
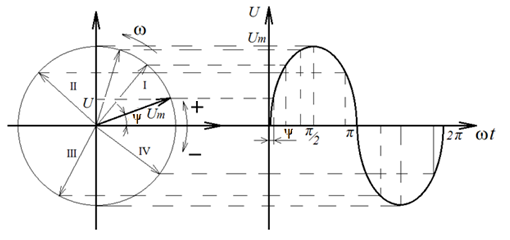
Рисунок 1.12 – Переход от синусоидальной формы представления гармонических величин к векторной.
Чтобы не изображать множественные положения вектора в различные моменты времени при построении векторных диаграмм изображается положение векторов соответствующее нулевому моменту времени.
Длина вектора – это амплитудное значение гармонически изменяющейся величины (например напряжения Um), а проекция вектора на вертикальную ось – мгновенное значение. Скорость вращения вектора определяется круговой частотой, за один период колебаний синусоиды вектор делает один полный оборот.
1.12 Операции над векторными величинами
Сложение двух векторов выполнить гораздо проще, чем сложение двух синусоид. Рассмотрим сложение э.д.с. двух последовательно включенных катушек. При сложении векторов используем правило параллелограмма. Результирующая э.д.с. представлена диагональю образованной фигуры. Длина полученного вектора соответствует величине суммарной э.д.с., суммарная э.д.с. имеет свой сдвиг по фазе.
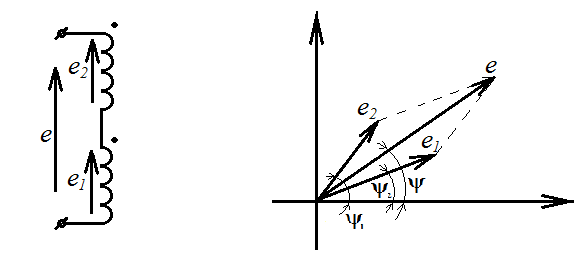
а б
Рисунок 1.13 – Векторное сложение э.д.с. двух катушек (а) – схема соединения катушек, (б) – векторная диаграмма
Таким образом, любой вектор задается двумя величинами: длиной и углом поворота. Для удобства вычислений под длиной вектора понимают не амплитуду синусоидальной функции, а действующее значение (напряжения или тока). Угол показывает сдвиг фазы относительно начала координат.
2.1 Магнитное поле
Вокруг любого движущегося электрического заряда (в том числе вокруг проводника с током) возникает магнитное поле. Причина возникновения магнитного поля – движущийся электрический заряд!
Магнитное поле принято условно обозначать силовыми линиями. Силовая линия это – линия, соединяющая точки, в которых вектор напряженности магнитного поля направлен по касательной. Силовые линии всегда замкнуты, никогда не пересекаются и могут распространяться в любой среде. Силовые линии магнитного поля стремятся замыкаться в плоскости перпендикулярной направлению тока.
Магнитное поле всегда представлено биполем (имеет два полюса). Полюсами называются точки, из которых выходят (северный полюс N) и в которые приходят (южный полюс S) силовые линии.
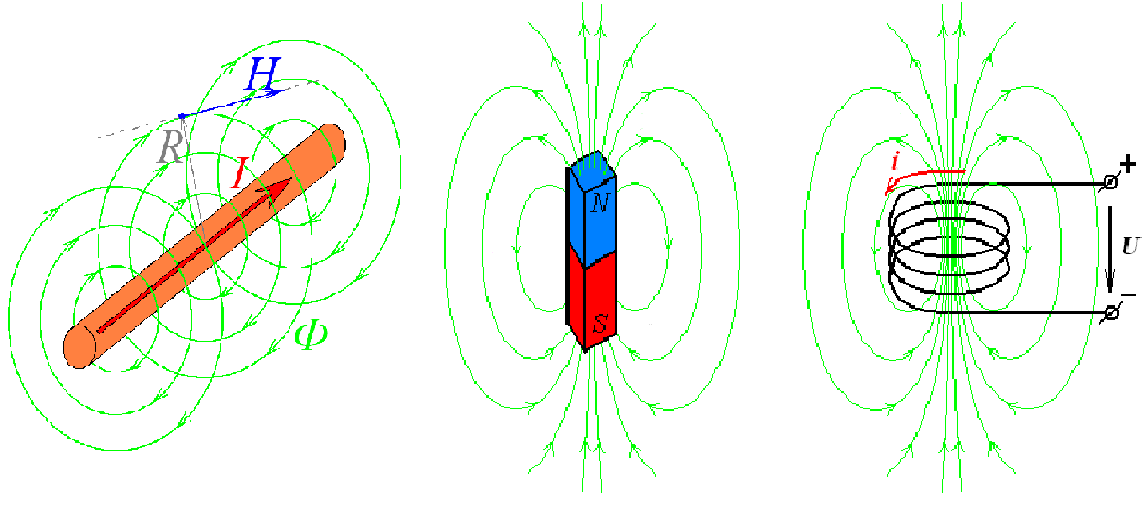
Рисунок 2.1 – источники магнитного поля
2.2 Параметры магнитного поля
Напряженность магнитного поля физическая величина, характеризующая его способность оказывать силовое действие на помещенную в данную точку поля единицу магнетизма. (Напряженность магнитного поля величина векторная, характеризуется не только численным значением, но и направлением).
Величину напряженности магнитного поля в конкретной точке определяет закон Био – Савара – Лапласа. Для линейного проводника с током, когда силовые линии будут представлять собой окружности, напряженность в точке удаленной на расстояние R (радиус окружности) от проводника определяется как:
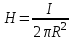
,
при этом, направление силовых линий определяется правилом буравчика (правоходового винта). При вращении винта по часовой стрелке (по направлению силовых линий поля) направление его линейного перемещения совпадает с направлением тока в проводнике.
В системе СИ единицей напряженности магнитного поля является Ампер деленное на метр [А/м].
Распространение магнитного поля в веществе, зависит от его свойств. Свойство вещества способствовать распространению силовых линий поля называется магнитной проницаемостью μ. Некий объем материала, помещенный в магнитное поле, будет не только проводить его через себя, но и усиливать или ослаблять. В зависимости от величины магнитной проницаемости все вещества делятся на три класса:
Диамагнетики – μ ≈ 1-0,00001<1 – при внесении в магнитное поле незначительно ослабляют его (к диамагнетикам относятся такие вещества как медь, золото…);
Парамагнетики – μ ≈ 1+0,00001>1 – незначительно усиливают магнитное поле (парамагнетики – алюминий, воздух…);
Ферромагнетики – μ >>1 – в сотни, тысячи раз усиливают магнитное поле (ферромагнетики – железо, сталь…, ферромагнетики, помещенные в магнитное поле, намагничиваются (приобретают собственное магнитное поле)).
Относительная магнитная проницаемость μ – величина безразмерная и показывает во сколько раз вещество усиливает или ослабляет магнитное поле относительно вакуума. Магнитная проницаемость вакуума принята за магнитную постоянную μ0 =4π·10-7 и имеет размерность Генри деленное на метр [Гн/м].
Произведение μ μ0 (иногда обозначается как μа) – называется абсолютной магнитной проницаемостью вещества.
Способность вещества усиливать или ослаблять магнитное поле при замещении вакуума этим веществом называется магнитной индукцией. Это силовая характеристика поля в точке среды. Единица измерения магнитной индукции Тесла [Тл].
B = μ μ0H
Так при размещении в магнитное поле стального изделия все силовые линии будут стремиться сосредоточиться в нем (в стали) и магнитное поле будет усиливаться. Поэтому силовые магнитные линии, распространяющиеся в веществе, еще называют линиями магнитной индукции.
Для обозначения линий магнитной индукции, сосредоточенных и распространяющихся в ферромагнитном сердечнике (магнитопроводе), используют термин –
магнитный поток. Если линии магнитной индукции пронизывают выделенный контур площадью s под прямым углом, то магнитный поток, ограниченный контуром будет определяться как произведение магнитной индукции на площадь контура (Рис. 2.2):
Ф=B·s.

а б
Рисунок 2.2 – понятие магнитного потока: определение магнитного потока (а), магнитный поток в замкнутом магнитопроводе (б)
Однако реальные магнитные поля чаще всего неравномерно в пространестве поэтому приведенная формула справедлива только для сердечников катушек, а например в металле формула будет иметь более сложный вид.
Единицей измерения магнитного потока является Вебер [Вб].1>
2.3 Магнитопроводы и их характеристики
Магнитопровод (сердечник) – это деталь электротехнического устройства, предназначенная для формирования магнитного потока, возбуждаемого токовыми обмотками этого устройства.
Изменяя конфигурацию магнитопровода можно получить магнитный поток любой формы. Так если проводник с током пропустить в центре стального кольца, то все линии магнитной индукции будут стремиться замыкаться в этом кольце, образуя магнитный поток (Рис. 2б).
Магнитопроводы изготавливаются из магнитомягких (с малыми значениями остаточной индукции и узкой петлей магнитного гистерезиса) ферромагнетиков и имеют различную форму, как правило замкнутую тороидальную, Ш – образную и др. В вихретоковых преобразователях сердечники служат для увеличения чувствительности преобразователя и увеличения локальности контроля.
Величина, характеризующая намагничивающее действие тока, протекающего в обмотке электротехнического устройства, называется магнитодвижущей силой (МДС). Для замкнутого магнитопровода МДС определяется как произведению тока, протекающего в обмотке, на число ее витков:
F = I·n.
Магнитное сопротивление среды характеризует способность вещества препятствовать распространению линий магнитной индукции – величина обратная магнитной проводимости. Магнитное сопротивление магнитопровода, кроме того, зависит от его геометрии – прямо пропорционально длине магнитопровода и обратно пропорционально площади его поперечного сечения и магнитной проницаемости материала магнитопровода.
2.4 Законы взаимодействия магнитного поля и электрического тока
2.4.1 Закон Био-Савара-Лапласса
Данный закон позволяет определить значение напряженности в конкретной точке магнитного поля, созданного током, протекающим в проводнике любой формы.
Для линейного проводника с током, когда силовые линии представляют собой окружности, напряженность магнитного поля на расстоянии R от проводника с протекающим в нем током I определяется:
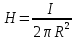
Рисунок 1.10 – понятие фазы колебаний
Приняв за начало отсчета момент начала колебаний одной из синусоидальных величин, изменяющихся с одной частотой (например напряжения) можно определить время (угол) отставания или опережения по фазе другой или других величин (например тока).

Рисунок 1.11 – Сдвиг фазы колебаний двух величин (а) – величины имеют одинаковую фазу (находятся в фазе), (б) – одна величина (ток) отстает по фазе на 900 (сдвиг по фазе), сдвиг по фазе составляет 1800 (величины находятся в противофазе)
1.11 Векторные диаграммы
Оперировать гармоническими величинами, представленными в виде синусоидальных функций, оценивая их взаимодействия, практически неудобно. Поэтому для анализа переменных электрических величин используют векторные диаграммы.
Гармонические функции при этом изображают векторами, вращающимися относительно начала прямоугольной системы координат, против часовой стрелки с угловой скоростью ω. При этом всегда можно осуществить переход от синусоиды к вектору и наоборот (рис. 1.12).

Рисунок 1.12 – Переход от синусоидальной формы представления гармонических величин к векторной.
Чтобы не изображать множественные положения вектора в различные моменты времени при построении векторных диаграмм изображается положение векторов соответствующее нулевому моменту времени.
Длина вектора – это амплитудное значение гармонически изменяющейся величины (например напряжения Um), а проекция вектора на вертикальную ось – мгновенное значение. Скорость вращения вектора определяется круговой частотой, за один период колебаний синусоиды вектор делает один полный оборот.
1.12 Операции над векторными величинами
Сложение двух векторов выполнить гораздо проще, чем сложение двух синусоид. Рассмотрим сложение э.д.с. двух последовательно включенных катушек. При сложении векторов используем правило параллелограмма. Результирующая э.д.с. представлена диагональю образованной фигуры. Длина полученного вектора соответствует величине суммарной э.д.с., суммарная э.д.с. имеет свой сдвиг по фазе.

а б
Рисунок 1.13 – Векторное сложение э.д.с. двух катушек (а) – схема соединения катушек, (б) – векторная диаграмма
Таким образом, любой вектор задается двумя величинами: длиной и углом поворота. Для удобства вычислений под длиной вектора понимают не амплитуду синусоидальной функции, а действующее значение (напряжения или тока). Угол показывает сдвиг фазы относительно начала координат.
-
Магнитные поля и их взаимодействие с электрическим током
2.1 Магнитное поле
Вокруг любого движущегося электрического заряда (в том числе вокруг проводника с током) возникает магнитное поле. Причина возникновения магнитного поля – движущийся электрический заряд!
Магнитное поле принято условно обозначать силовыми линиями. Силовая линия это – линия, соединяющая точки, в которых вектор напряженности магнитного поля направлен по касательной. Силовые линии всегда замкнуты, никогда не пересекаются и могут распространяться в любой среде. Силовые линии магнитного поля стремятся замыкаться в плоскости перпендикулярной направлению тока.
Магнитное поле всегда представлено биполем (имеет два полюса). Полюсами называются точки, из которых выходят (северный полюс N) и в которые приходят (южный полюс S) силовые линии.

Рисунок 2.1 – источники магнитного поля
2.2 Параметры магнитного поля
Напряженность магнитного поля физическая величина, характеризующая его способность оказывать силовое действие на помещенную в данную точку поля единицу магнетизма. (Напряженность магнитного поля величина векторная, характеризуется не только численным значением, но и направлением).
Величину напряженности магнитного поля в конкретной точке определяет закон Био – Савара – Лапласа. Для линейного проводника с током, когда силовые линии будут представлять собой окружности, напряженность в точке удаленной на расстояние R (радиус окружности) от проводника определяется как:
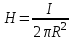
,
при этом, направление силовых линий определяется правилом буравчика (правоходового винта). При вращении винта по часовой стрелке (по направлению силовых линий поля) направление его линейного перемещения совпадает с направлением тока в проводнике.
В системе СИ единицей напряженности магнитного поля является Ампер деленное на метр [А/м].
Распространение магнитного поля в веществе, зависит от его свойств. Свойство вещества способствовать распространению силовых линий поля называется магнитной проницаемостью μ. Некий объем материала, помещенный в магнитное поле, будет не только проводить его через себя, но и усиливать или ослаблять. В зависимости от величины магнитной проницаемости все вещества делятся на три класса:
Диамагнетики – μ ≈ 1-0,00001<1 – при внесении в магнитное поле незначительно ослабляют его (к диамагнетикам относятся такие вещества как медь, золото…);
Парамагнетики – μ ≈ 1+0,00001>1 – незначительно усиливают магнитное поле (парамагнетики – алюминий, воздух…);
Ферромагнетики – μ >>1 – в сотни, тысячи раз усиливают магнитное поле (ферромагнетики – железо, сталь…, ферромагнетики, помещенные в магнитное поле, намагничиваются (приобретают собственное магнитное поле)).
Относительная магнитная проницаемость μ – величина безразмерная и показывает во сколько раз вещество усиливает или ослабляет магнитное поле относительно вакуума. Магнитная проницаемость вакуума принята за магнитную постоянную μ0 =4π·10-7 и имеет размерность Генри деленное на метр [Гн/м].
Произведение μ μ0 (иногда обозначается как μа) – называется абсолютной магнитной проницаемостью вещества.
Способность вещества усиливать или ослаблять магнитное поле при замещении вакуума этим веществом называется магнитной индукцией. Это силовая характеристика поля в точке среды. Единица измерения магнитной индукции Тесла [Тл].
B = μ μ0H
Так при размещении в магнитное поле стального изделия все силовые линии будут стремиться сосредоточиться в нем (в стали) и магнитное поле будет усиливаться. Поэтому силовые магнитные линии, распространяющиеся в веществе, еще называют линиями магнитной индукции.
Для обозначения линий магнитной индукции, сосредоточенных и распространяющихся в ферромагнитном сердечнике (магнитопроводе), используют термин –
магнитный поток. Если линии магнитной индукции пронизывают выделенный контур площадью s под прямым углом, то магнитный поток, ограниченный контуром будет определяться как произведение магнитной индукции на площадь контура (Рис. 2.2):
Ф=B·s.

а б
Рисунок 2.2 – понятие магнитного потока: определение магнитного потока (а), магнитный поток в замкнутом магнитопроводе (б)
Однако реальные магнитные поля чаще всего неравномерно в пространестве поэтому приведенная формула справедлива только для сердечников катушек, а например в металле формула будет иметь более сложный вид.
Единицей измерения магнитного потока является Вебер [Вб].1>
2.3 Магнитопроводы и их характеристики
Магнитопровод (сердечник) – это деталь электротехнического устройства, предназначенная для формирования магнитного потока, возбуждаемого токовыми обмотками этого устройства.
Изменяя конфигурацию магнитопровода можно получить магнитный поток любой формы. Так если проводник с током пропустить в центре стального кольца, то все линии магнитной индукции будут стремиться замыкаться в этом кольце, образуя магнитный поток (Рис. 2б).
Магнитопроводы изготавливаются из магнитомягких (с малыми значениями остаточной индукции и узкой петлей магнитного гистерезиса) ферромагнетиков и имеют различную форму, как правило замкнутую тороидальную, Ш – образную и др. В вихретоковых преобразователях сердечники служат для увеличения чувствительности преобразователя и увеличения локальности контроля.
Величина, характеризующая намагничивающее действие тока, протекающего в обмотке электротехнического устройства, называется магнитодвижущей силой (МДС). Для замкнутого магнитопровода МДС определяется как произведению тока, протекающего в обмотке, на число ее витков:
F = I·n.
Магнитное сопротивление среды характеризует способность вещества препятствовать распространению линий магнитной индукции – величина обратная магнитной проводимости. Магнитное сопротивление магнитопровода, кроме того, зависит от его геометрии – прямо пропорционально длине магнитопровода и обратно пропорционально площади его поперечного сечения и магнитной проницаемости материала магнитопровода.
2.4 Законы взаимодействия магнитного поля и электрического тока
2.4.1 Закон Био-Савара-Лапласса
Данный закон позволяет определить значение напряженности в конкретной точке магнитного поля, созданного током, протекающим в проводнике любой формы.
Для линейного проводника с током, когда силовые линии представляют собой окружности, напряженность магнитного поля на расстоянии R от проводника с протекающим в нем током I определяется: