ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 128
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Напряженность поля в центре единочного витка радиусом R с протекающим в нем током I:
.
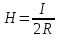В центре соленоида с геометрическими размерами l > 4R >> dи протекающим в нем током I:
,
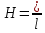где l – длина соленоида, R – радиус соленоида, d – толщина слоев намотки, n – число витков.
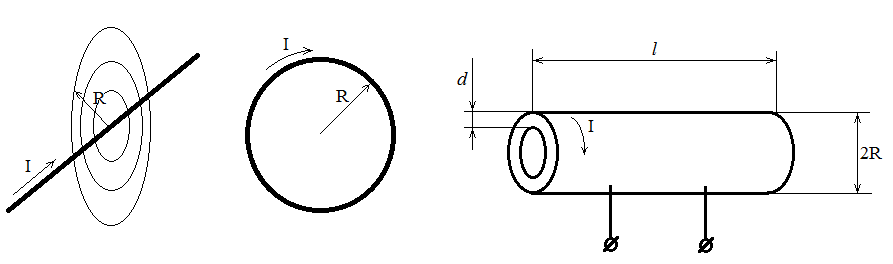
а б в
Рисунок 2.3 – к определению напряженности магнитного поля, созданного линейным проводником с током (а), единичным витком с током (б), соленоидом (в)
2.4.2 Закон Ампера
На проводник с протекающим в нем током, помещенный в магнитное поле действует сила, стремящаяся вытолкнуть проводник из поля (сила Ампера). Это явление демонстрирует электромеханическое действие магнитного поля и объясняется силовым взаимодействием между магнитным полем создаваемым током, протекающим в проводнике, с одной стороны и магнитным полем в которое помещен проводник, с другой. Величина силы, действующей со стороны поля на проводник с током, определяется законом Ампера:
F=BIlsinα,
где В – магнитная индукция, I – сила тока в проводнике, l – длина проводника, α– угол между вектором магнитной индукции и направлением тока.
Направление действия силы Ампера определяется правилом левой руки.
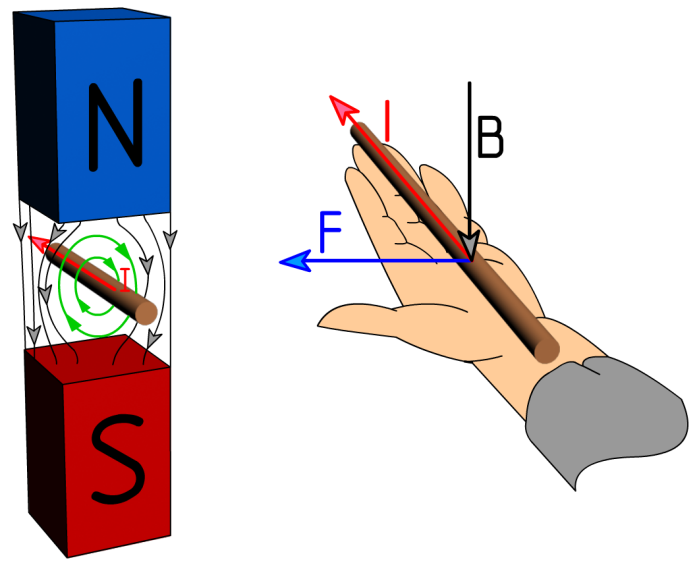
Рисунок 2.4 – сила Ампера
2.4.3 Закон электромагнитной индукции
В любом токопроводящем контуре (как в замкнутом, так и в разомкнутом), находящемся под действием изменяющегося с течением времени (переменном) магнитном потоке, возникает электро-движущая сила – э.д.с. Это явление демонстрирует индукционное действие магнитного поля и описывается законом электромагнитной индукции – величина э.д.с. равна скорости изменения магнитного потока, взятой со знаком минус:
.
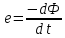где е – э.д.с., Ф – магнитный поток, t – время,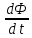
– первая производная от магнитного потока по времени (скорость изменения магнитного потока).
Так в проводнике, движущемся в магнитном поле будет создаваться Э.Д.С., направление которой определяется правилом правой руки.
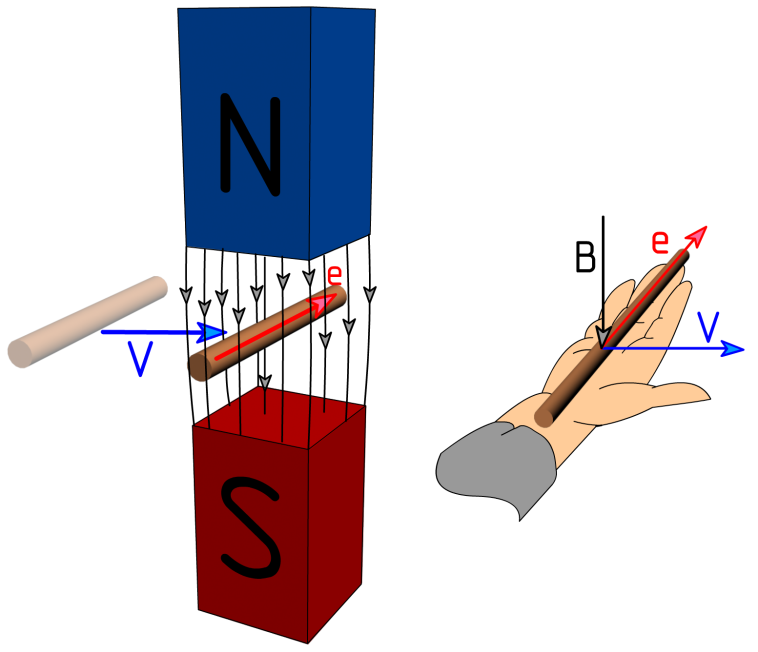
Рисунок 2.5 – возникновение Э.Д.С. в проводнике, движущемся со скоростью V в магнитном поле с индукцией В
2.4.4 Правило Ленца. Коэффициент взаимоиндукции
Знак минус, применяемый в законе электромагнитной индукции, выражает правило Ленца, которое можно трактовать для различных случаев электромагнитных взаимодействий. Так если контур, помещенный под действие переменное магнитного потока, будет замкнут, то возникающий в нем под действием наведенной Э.Д.С. ток создаст такой магнитный поток, направление которого будет противоположно направлению первичного потока.
Или если катушку подключить к источнику переменного напряжения, то магнитный поток, созданный протекающим через нее током, наведет в витках катушки Э.Д.С. самоиндукции, направленную встречно напряжению источника и значит ограничивающей ток в катушке.
В системе, состоящей из двух индуктивно связанных катушек, будут наблюдаться подобные взаимодействия (рис. 2.6).
Если одну из катушек подключить к источнику переменного напряжения, то магнитный поток, созданный протекающим через нее током, наведет в витках другой катушки Э.Д.С. взаимоиндукции. Если замкнуть цепь второй катушки, то ток, возникающий под действием этой Э.Д.С. будет создавать магнитный поток, направленный встречно первичному потоку.
Степень взаимного влияния двух индуктивно связанных систем определяется коэффициентом взаимоиндукции. Коэффициент взаимоиндукции определяется магнитным потоком, создаваемым током одного контура и пронизывающим другой контур.
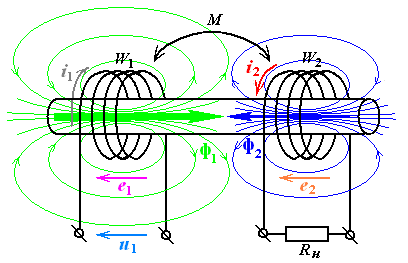
Рисунок 2.6 – явление взаимоиндукции, возникающее между двумя индуктивно связанными катушками W1 и W2 с коэффициентом взаимоиндукции М.
2.5 Индукционные (вихревые) токи. Поле, создаваемое индукционным током
В любом замкнутом токопроводящем контуре (короткозамкнутый виток, объем токопроводящего материала, катушка с подключенным к ее зажимам сопротивлением нагрузки и т.п.), согласно закона электромагнитной индукции
, возникает индукционный
(наведенный) ток.
Индукционные токи в массивных объемах токопроводящих материалов (например в магнитопроводах электротехнических устройств), замкнутые по кольцевым траекториям, лежащим в плоскости перпендикулярной направлению магнитного потока получили название – вихревые токи или токи Фуко.
Индукционные токи создают создают собственное магнитное поле. Магнитный поток индукционных токов (токов Фуко), согласно правилу Ленца, всегда направлен встречно (находится в противофазе) основному магнитному потоку.
2.6 Индуктивное сопротивление
Учитывая то обстоятельство, что электрический ток порождает вокруг себя магнитное поле (по закону Био-Савара-Лапласа), а если ток и, следовательно, магнитное поле переменные, то оно в свою очередь порождает электродвижущую силу (согласно закону электромагнитной индукции), которая накладывается на напряжение и изменяет его то энергетические потери такого взаимодействия описываются индуктивным сопротивлением XL. У обычных проводинков с током оно незначительно, а вот в катушках оно играет большую роль и, часто, гораздо больше активного сопротивления.
Индуктивное сопротивление катушки определяется формулой:
,
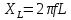где это сопротивление зависит от частоты колебаний fи индуктивности катушки L. Индуктивность катушки определяется ее параметрами и магнитной проницаемостью внутри нее:
,
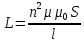где n – количество витков катушки; S – в данном случае площадь охватываемая катушкой; - относительная магнитная проницаемость среды внутри катушки; l – длина катушки. Так на индуктивность можно влиять геометрическими параметрами катушки и магнитной проницаемостью сердечника, вставляемого внутрь. Сердечник обычно выполняют из магнитомягкого материала с высокой проницаемостью, что приводит к большой индуктивности, а значит к высоким индуктивному сопротивлению катушки и ее чувствительности к изменениям внешних параметров, что и используется в вихретоковом контроле.
3. ВИХРЕВые ТОКи в электропроводящих материалах
3.1 Распределение вихревого тока
Вихревые токи (токи Фуко) это замкнутые электрические токи, возникающие в объеме токопроводящего материала под воздействием переменного магнитного потока. Вихревые токи являются индукционными токами и в отличие от токов, протекающих в проводах (обмотках, токоведущих жилах и пр.) по строго определенным направлениям, замыкаются в объеме токопроводящей среды, как правило, по кольцевым (вихревым) траекториям.
Основным параметром вихревых токов является их плотность.
Плоскость вихревых токов всегда перпендикулярна направлению возбуждающего их магнитного потока. Если магнитный поток пронизывает плоский проводник нормально его плоскости, как показано на рисунке 3.1 а, то в проводнике возникают вихревые токи. В случае если магнитный поток пронизывает проводник вдоль его плоскости, как показано на рисунке 3.1 б – вихревые токи не возникают.
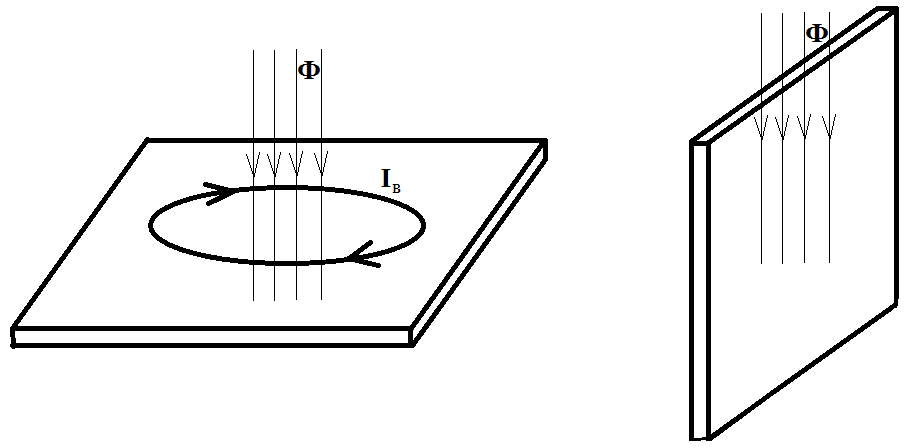
а б
Рисунок 3.1 – Возбуждение вихревых токов в плоском проводнике: магнитный поток направлен нормально плоскости проводника и вызывает возникновение вихревых токов (а), магнитный поток направлен вдоль плоскости проводника, вихревые токи не возникают (б)
Исходя из этого, для уменьшения влияния вихревых токов на работу электрических машин (например трансформатора) их сердечники выполняют из пластин электротехнической стали, изолированных друг от друга слоями лака. Этот же эффект дробления вихревых токов положен в основу вихретоковой дефектоскопии, когда дефект (трещина) выступает в роли изолирующего слоя и дробит вихревые токи (рис.2)
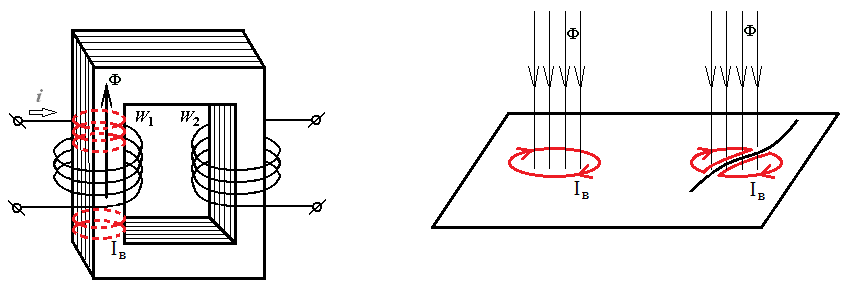
а б
Рисунок 3.2 – дробление вихревых токов: принудительное в сердечнике трансформатора (а); дефектом при вихретоковой дефектоскопии (б)
3.2 Изменение амплитуды и фазы тока
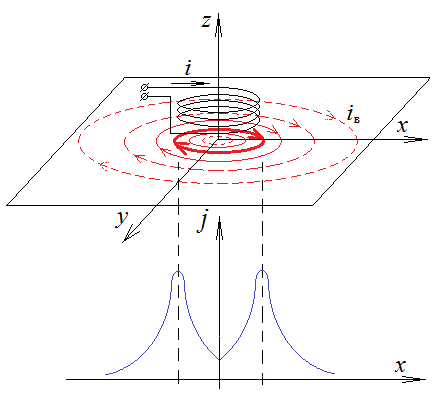
Плотность вихревых токов в массиве токопроводящего материала не равномерна (рис. 3.3). Распределение вихревых токов по объему токопроводящей среды сопровождается изменением амплитуды и фазы. Так при возбуждении вихревых токов в листе металла катушкой с протекающим по ее виткам током максимальная плотность вихревых токов будет наблюдаться в поверхностном слое объекта непосредственно под витками катушки. При удалении вдоль поверхности от витков катушки плотность вихревых токов будет уменьшаться по закону близкому к экспоненциальному. Также с увеличением глубины вихревые токи больше отстают по фазе от поверхностных.
а б
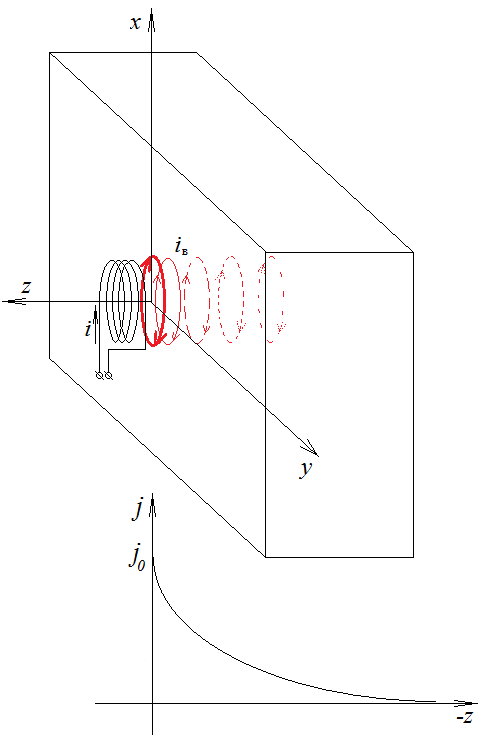
Рисунок 3.3 – распределение плотности вихревых токов в токопроводящей среде: в поверхностном слое (а); по глубине объекта (б)
При анализе распределения вихревых токов по глубине объекта можно наблюдать уменьшение амплитуды с ростом глубины, подчиняющееся экспоненциальному закону:
ј = ј0·е-mz,
где ј0– плотность вихревых токов на поверхности объекта, m – коэффициент затухания, зависящий от электромагнитных свойств объекта и частоты тока катушки. Также наблюдается изменение фазы вихревых токов. С увеличением глубины фаза тока в более глубоких слоях все больше отстает от тока в поверхностном слое.
3.3 Глубина проникновения вихревых токов
Глубина вихревых токов зависит от величины возбуждающего их магнитного потока, частоты возбуждения и электромагнитных свойств материала объекта. Для оценки глубины вихревых токов используют относительную величину – условную глубину проникновения вихревых токов. Условная глубина проникновения вихревых токов – это расстояние от поверхности объекта контроля (где наблюдается максимальная плотность вихревых токов) до слоя в котором плотность уменьшается в е раз (е ≈ 2,71 – основание натурального логарифма):
,
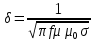где f – частота тока возбуждения,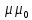
– абсолютная магнитная проницаемость материала объекта, σ – удельная электрическая проводимость материала объекта.
Условная глубина не зависит от величины магнитного потока (геометрии возбуждающей катушки, наличия сердечника, зазора между катушкой и объектом и т.п.). С увеличением частоты возбуждения глубина проникновения вихревых токов уменьшается. Вихревые токи выталкиваются к поверхности объекта. Такой же эффект наблюдается при возбуждении вихревых токов в ферромагнитных материалах (конструкционных сталях), у которых влияние магнитной проницаемости на глубину проникновения во много раз больше чем влияние удельной электрической проводимости, как правило меньшей чем у меди, алюминия и сплавов на их основе.
Напряженность поля в центре единочного витка радиусом R с протекающим в нем током I:
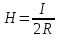.В центре соленоида с геометрическими размерами l > 4R >> dи протекающим в нем током I:
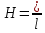,где l – длина соленоида, R – радиус соленоида, d – толщина слоев намотки, n – число витков.
а б в
Рисунок 2.3 – к определению напряженности магнитного поля, созданного линейным проводником с током (а), единичным витком с током (б), соленоидом (в)
2.4.2 Закон Ампера
На проводник с протекающим в нем током, помещенный в магнитное поле действует сила, стремящаяся вытолкнуть проводник из поля (сила Ампера). Это явление демонстрирует электромеханическое действие магнитного поля и объясняется силовым взаимодействием между магнитным полем создаваемым током, протекающим в проводнике, с одной стороны и магнитным полем в которое помещен проводник, с другой. Величина силы, действующей со стороны поля на проводник с током, определяется законом Ампера:
F=BIlsinα,
где В – магнитная индукция, I – сила тока в проводнике, l – длина проводника, α– угол между вектором магнитной индукции и направлением тока.
Направление действия силы Ампера определяется правилом левой руки.
Рисунок 2.4 – сила Ампера
2.4.3 Закон электромагнитной индукции
В любом токопроводящем контуре (как в замкнутом, так и в разомкнутом), находящемся под действием изменяющегося с течением времени (переменном) магнитном потоке, возникает электро-движущая сила – э.д.с. Это явление демонстрирует индукционное действие магнитного поля и описывается законом электромагнитной индукции – величина э.д.с. равна скорости изменения магнитного потока, взятой со знаком минус:
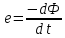.где е – э.д.с., Ф – магнитный поток, t – время,
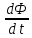– первая производная от магнитного потока по времени (скорость изменения магнитного потока).Так в проводнике, движущемся в магнитном поле будет создаваться Э.Д.С., направление которой определяется правилом правой руки.
Рисунок 2.5 – возникновение Э.Д.С. в проводнике, движущемся со скоростью V в магнитном поле с индукцией В
2.4.4 Правило Ленца. Коэффициент взаимоиндукции
Знак минус, применяемый в законе электромагнитной индукции, выражает правило Ленца, которое можно трактовать для различных случаев электромагнитных взаимодействий. Так если контур, помещенный под действие переменное магнитного потока, будет замкнут, то возникающий в нем под действием наведенной Э.Д.С. ток создаст такой магнитный поток, направление которого будет противоположно направлению первичного потока.
Или если катушку подключить к источнику переменного напряжения, то магнитный поток, созданный протекающим через нее током, наведет в витках катушки Э.Д.С. самоиндукции, направленную встречно напряжению источника и значит ограничивающей ток в катушке.
В системе, состоящей из двух индуктивно связанных катушек, будут наблюдаться подобные взаимодействия (рис. 2.6).
Если одну из катушек подключить к источнику переменного напряжения, то магнитный поток, созданный протекающим через нее током, наведет в витках другой катушки Э.Д.С. взаимоиндукции. Если замкнуть цепь второй катушки, то ток, возникающий под действием этой Э.Д.С. будет создавать магнитный поток, направленный встречно первичному потоку.
Степень взаимного влияния двух индуктивно связанных систем определяется коэффициентом взаимоиндукции. Коэффициент взаимоиндукции определяется магнитным потоком, создаваемым током одного контура и пронизывающим другой контур.
Рисунок 2.6 – явление взаимоиндукции, возникающее между двумя индуктивно связанными катушками W1 и W2 с коэффициентом взаимоиндукции М.
2.5 Индукционные (вихревые) токи. Поле, создаваемое индукционным током
В любом замкнутом токопроводящем контуре (короткозамкнутый виток, объем токопроводящего материала, катушка с подключенным к ее зажимам сопротивлением нагрузки и т.п.), согласно закона электромагнитной индукции
, возникает индукционный
(наведенный) ток.
Индукционные токи в массивных объемах токопроводящих материалов (например в магнитопроводах электротехнических устройств), замкнутые по кольцевым траекториям, лежащим в плоскости перпендикулярной направлению магнитного потока получили название – вихревые токи или токи Фуко.
Индукционные токи создают создают собственное магнитное поле. Магнитный поток индукционных токов (токов Фуко), согласно правилу Ленца, всегда направлен встречно (находится в противофазе) основному магнитному потоку.
2.6 Индуктивное сопротивление
Учитывая то обстоятельство, что электрический ток порождает вокруг себя магнитное поле (по закону Био-Савара-Лапласа), а если ток и, следовательно, магнитное поле переменные, то оно в свою очередь порождает электродвижущую силу (согласно закону электромагнитной индукции), которая накладывается на напряжение и изменяет его то энергетические потери такого взаимодействия описываются индуктивным сопротивлением XL. У обычных проводинков с током оно незначительно, а вот в катушках оно играет большую роль и, часто, гораздо больше активного сопротивления.
Индуктивное сопротивление катушки определяется формулой:
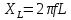,где это сопротивление зависит от частоты колебаний fи индуктивности катушки L. Индуктивность катушки определяется ее параметрами и магнитной проницаемостью внутри нее:
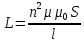,где n – количество витков катушки; S – в данном случае площадь охватываемая катушкой; - относительная магнитная проницаемость среды внутри катушки; l – длина катушки. Так на индуктивность можно влиять геометрическими параметрами катушки и магнитной проницаемостью сердечника, вставляемого внутрь. Сердечник обычно выполняют из магнитомягкого материала с высокой проницаемостью, что приводит к большой индуктивности, а значит к высоким индуктивному сопротивлению катушки и ее чувствительности к изменениям внешних параметров, что и используется в вихретоковом контроле.
3. ВИХРЕВые ТОКи в электропроводящих материалах
3.1 Распределение вихревого тока
Вихревые токи (токи Фуко) это замкнутые электрические токи, возникающие в объеме токопроводящего материала под воздействием переменного магнитного потока. Вихревые токи являются индукционными токами и в отличие от токов, протекающих в проводах (обмотках, токоведущих жилах и пр.) по строго определенным направлениям, замыкаются в объеме токопроводящей среды, как правило, по кольцевым (вихревым) траекториям.
Основным параметром вихревых токов является их плотность.
Плоскость вихревых токов всегда перпендикулярна направлению возбуждающего их магнитного потока. Если магнитный поток пронизывает плоский проводник нормально его плоскости, как показано на рисунке 3.1 а, то в проводнике возникают вихревые токи. В случае если магнитный поток пронизывает проводник вдоль его плоскости, как показано на рисунке 3.1 б – вихревые токи не возникают.
а б
Рисунок 3.1 – Возбуждение вихревых токов в плоском проводнике: магнитный поток направлен нормально плоскости проводника и вызывает возникновение вихревых токов (а), магнитный поток направлен вдоль плоскости проводника, вихревые токи не возникают (б)
Исходя из этого, для уменьшения влияния вихревых токов на работу электрических машин (например трансформатора) их сердечники выполняют из пластин электротехнической стали, изолированных друг от друга слоями лака. Этот же эффект дробления вихревых токов положен в основу вихретоковой дефектоскопии, когда дефект (трещина) выступает в роли изолирующего слоя и дробит вихревые токи (рис.2)
а б
Рисунок 3.2 – дробление вихревых токов: принудительное в сердечнике трансформатора (а); дефектом при вихретоковой дефектоскопии (б)
3.2 Изменение амплитуды и фазы тока
Плотность вихревых токов в массиве токопроводящего материала не равномерна (рис. 3.3). Распределение вихревых токов по объему токопроводящей среды сопровождается изменением амплитуды и фазы. Так при возбуждении вихревых токов в листе металла катушкой с протекающим по ее виткам током максимальная плотность вихревых токов будет наблюдаться в поверхностном слое объекта непосредственно под витками катушки. При удалении вдоль поверхности от витков катушки плотность вихревых токов будет уменьшаться по закону близкому к экспоненциальному. Также с увеличением глубины вихревые токи больше отстают по фазе от поверхностных.
а б
Рисунок 3.3 – распределение плотности вихревых токов в токопроводящей среде: в поверхностном слое (а); по глубине объекта (б)
При анализе распределения вихревых токов по глубине объекта можно наблюдать уменьшение амплитуды с ростом глубины, подчиняющееся экспоненциальному закону:
ј = ј0·е-mz,
где ј0– плотность вихревых токов на поверхности объекта, m – коэффициент затухания, зависящий от электромагнитных свойств объекта и частоты тока катушки. Также наблюдается изменение фазы вихревых токов. С увеличением глубины фаза тока в более глубоких слоях все больше отстает от тока в поверхностном слое.
3.3 Глубина проникновения вихревых токов
Глубина вихревых токов зависит от величины возбуждающего их магнитного потока, частоты возбуждения и электромагнитных свойств материала объекта. Для оценки глубины вихревых токов используют относительную величину – условную глубину проникновения вихревых токов. Условная глубина проникновения вихревых токов – это расстояние от поверхности объекта контроля (где наблюдается максимальная плотность вихревых токов) до слоя в котором плотность уменьшается в е раз (е ≈ 2,71 – основание натурального логарифма):
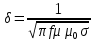,где f – частота тока возбуждения,
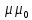– абсолютная магнитная проницаемость материала объекта, σ – удельная электрическая проводимость материала объекта.Условная глубина не зависит от величины магнитного потока (геометрии возбуждающей катушки, наличия сердечника, зазора между катушкой и объектом и т.п.). С увеличением частоты возбуждения глубина проникновения вихревых токов уменьшается. Вихревые токи выталкиваются к поверхности объекта. Такой же эффект наблюдается при возбуждении вихревых токов в ферромагнитных материалах (конструкционных сталях), у которых влияние магнитной проницаемости на глубину проникновения во много раз больше чем влияние удельной электрической проводимости, как правило меньшей чем у меди, алюминия и сплавов на их основе.