Для формирования интереса  к изучению предмета  следует создавать  производственные проблемные ситуации, которые решаются при помощи математических знаний и умений. Изучение сложного математического материала становится  более интересным,  если студенты видят практическое применение изучаемых тем непосредственно в своей профессиональной деятельности. Решение задач с производственной направленностью способствует формированию у студентов способностей находить в профессиональной ситуации существенные признаки математического понятия, подводить объект под  математическое понятие, использовать его в новых условиях.       В процессе решения  предусматривается совершенствование рационального  применения теоретических знаний к решению практических задач, развития пространственного воображения и вычислительных навыков,  организации  самостоятельной работы с измерительными приборами, таблицами, справочной литературой. Видение возможности реализации приобретаемых знаний способствует развитию мотивации к обучению и достижению успеха. Таким образом, решение задач профессионального характера на уроках способствует развитию интереса к математике как к науке и как к профессионально значимой дисциплине, показывает прикладной, реально ощутимый характер математики. Студенты понимают, что математика – важный предмет в их образовании. Любая конструкция, любой технологический процесс требует расчетов, порой содержащих больше математики, чем техники.2. Методические вопросы темы.2.1. Построения методики применения практико-ориентированных задач.Профессионально значимые знания и умения являются основой построения методики применения практико-ориентированных задач. Задачи с профессиональной направленностью создаются на основе тех знаний и умений по математике, которые непосредственно или опосредованно связаны с профессиональными знаниями и умениями. В учебном заведении за ними закрепилось название профессионально значимых. Одним из главных условий построения методики применения задач по математике с профессиональной направленностью является отбор совокупности этих знаний и умений.Решение задач профессионального отбора следует начинать с понимания того, какие именно требования предъявляются к человеку данной профессии, какими видами деятельности ему предстоит овладеть.Профессионально значимые знания и умения по математике могут применяться в «готовом виде» для формирования на их основе профессиональных умений и навыков, теоретического обоснования практических действий и т.д. Эти знания помогают осмыслить сущность той или иной производственной операции; понять принципы устройства и действия орудий труда, справедливость требования безопасности труда.

---

Существуют профессионально значимые математические знания, которые первоначально вводятся, а затем формируются не только на уроках математики, но и на уроках других предметов естественно - математического цикла (физике, географии и т.д.). Они служат для лучшего осознания обучающимися производственных процессов, операций, для повышения их профессиональной грамотности.Ряд профессионально значимых знаний и умений могут первоначально формироваться на предметах профессионально-технического цикла, затем обогащаться и уточняться на уроках математики. Профессионально значимые математические знания и умения могут первоначально вводится на уроках математики, а формироваться и применяться на уроках математики, профессиональных дисциплинах и производственном обучении.Таким образом, применение задач с профессиональной направленностью требует выявления признаков профессионально значимых знаний и умений, а также отбора (согласно этим признакам и требованиям к отбору) совокупности знаний и умений из курса математики, значимых для данной профессии. Установление этапов межпредметного и межциклового формирования выделенных знаний подтвердило положение о необходимости соблюдения преемственности в процессе их изучения и обозначило место введения дидактических материалов с профессиональной направленностью в структуре урока, а именно при актуализации основных знаний и умений, формировании и закреплении новых понятий и способов действий.2.2. Разработка практико-ориентированных задач.Практика показывает, что студенты с интересом решают и воспринимают задачи практического содержания.  К задаче следует предъявлять следующие требования:

• 
  задачи должны соответствовать программе курса, вводиться в процесс обучения как необходимый компонент, служить достижению цели обучения;
  
• 
  вводимые в задачу понятия, термины должны быть доступными для студентов, содержание и требование задачи должны «сближаться с реальной действительностью»;
  
• 
  способы и методы решения задачи должны быть приближены к практическим приемам и методам;
  
• 
  прикладная часть задачи не должна покрывать ее математическую сущность;
  
• 
  текст задачи должен отражать реализацию межцикловых и межпредметных связей.
  

Практико-ориентированные задачи могут быть использованы с разной дидактической целью: они могут заинтересовать или мотивировать, развивать умственную деятельность, формировать практические умения и навыки, объяснять соотношение между математикой и другими дисциплинами. Решение задач с практическим содержанием могут быть предложены учащимся на различных этапах обучения. Решение задач на этапах восприятия  и осмысления нового материала имеет целью пробудить у студентов потребность в расширении знаний, познавательный интерес и научить их методам самостоятельного приобретения знаний. Решая и анализируя задачи на этапах закрепления и повторения учебного материала, учащиеся овладевают способами применения знаний на практике и вместе с тем более глубоко усваивают его содержание. При проверке усвоения программного материала решение задач с производственным содержанием позволяет установить, насколько прочно и глубоко его усвоили. Решение всех задач проходит в четыре эта­па.

---

1.Анализ условия задачи. Задача формулиру­ется на описательном языке. От правильной постановки задачи, указания ресурсов, которыми мы располагаем, зависит успеш­ность ее решения. Этому нужно учиться каждому так как пригодится специалисту любого профиля.2.Построение математической модели задачи.
Перевод исходной задачи на математический язык: вводятся переменные, ищутся связи между ними и устанавливаются ограничения на них, которые записываются в виде уравнений, неравенств или их систем. Любая математическая задача — модель каких-то прикладных задач (экономических, физических, биологических, технических и т.п.).3. Решение математической модели задачи.Изучается полученная модель. Если задача извест­ная, то она решается по соответствующему ей алго­ритму. Если задача никогда не решалась, то ищется необходимый алгоритм.4.Интерпретация решения. Это перевод реше­ния задачи на исходный язык.Рассмотрим пример практико-ориентированной задачи. Например, задачу связанную с конусом.Сначала обсуждается одна из ситуаций, в которой фигурирует объект, имеющий форму конуса (это куча зерна), ищется решение проблемы измерения необходимых для решения задачи величин.Задача. Найти объем кучи зерна.— Будем считать, что куча зерна имеет форму конуса. Какие элементы конуса необходимо знать, чтобы вычислить искомые величины? (Радиус основания, длину образующей и высоту конуса).— Высоту и радиус основания невозможно найти непосредственным измерением. Как найти радиус основания в этом случае? (Пусть у нас имеется, например, мягкая метровая лента. Измерим ею длину окружности основания кучи зерна и разделим это число на 2π).— Каким образом можно измерить длину образующей?( Перекинув метровую ленту через вершину кучи, мы определим длину двух образующих. Разделим ее на 2).— Осталось определить высоту кучи зерна. (Зная радиус и длину образующей, вычислим по теореме Пифагора высоту кучи зерна). — Теперь мы можем вычислить площадь поверхности и объем кучи зерна. После измерения получили: длина окружности кучи зерна равна 7,2 м. Длина двух образующих — 2,6 м. Найдите объем этой кучи, считая π = 3.— Вычислим радиус основания конуса: Длина одной образующей равна 1,3 м. Высоту конуса вычислим по теореме Пифагора

---

Тогда Далее можно предложить вычислить массу зерна.Итак, задачи с профессиональной направленностью служат средством управления познавательной деятельностью обучающихся. Они применяются на любом из этапов процесса формирования профессионально значимых математических понятий и теоретических утверждений: могут быть задействованы на уроке до, после и одновременно с введением новых знаний.3. Этапы реализации проекта.3.1.Наподготовительном этапе были проведены.

• 
  Анализ федеральных государственных образовательных стандартов, изучение и обобщение педагогического опыта, анализ имеющейся литературы, программно-методической документации, учебных планов, индивидуальных разработок.
  
• 
  Разработка дидактических материалов
  

В результате были определены основные параметры исследования, проблема, его предмет, методы. 3.2. В период организационно-практического этапа выявлялись и систематизировались педагогические условия для реализации проекта, создавалась программа обучающего эксперимента; осуществлялась проверка гипотезы и обобщение полученных экспериментальных данных, их математическая обработка. Так были проведены анкетирование студентов, различные диагностики с целью выявления уровня познавательного интереса и мотивации обучения, входные проверочные работы, в которые были включены не только задачи, решаемые с помощью математического моделирования, но и занимательные задачи, и задачи на решение жизненных ситуаций, практико-ориентированных задач.Таблица 1Мотивация
деятельности студентов на уроке

	Сентябрь 2016	Декабрь 2016
Учение по необходимости	28	24
Интерес к предмету	19	23
Повышенный познавательный интерес	2	3
Ситуативный интерес	51	50

---

Диаграмма 1Мотивация
деятельности студентов на урокеТаблица 2Результаты
контрольных работ на 1 курсе

	Успеваем.%	Качество знаний,%
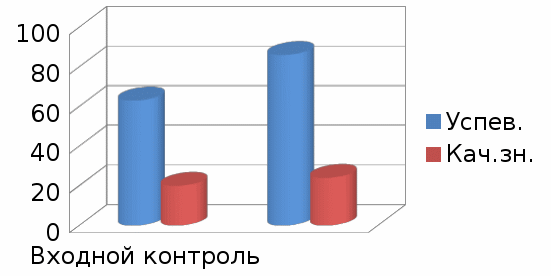
Входной контроль	63	20
Контрольная работа, декабрь16	86	24

Диаграмма 2Результаты
контрольных работ на 1 курсеБыли составлены задачи с профессиональной направленностью и другие практико-ориентированные задачи (Приложения 1-3)3.3.Обобщающе-практический этап.Анализ, систематизация и обобщение исследования были осуществлены на обобщающе-практическом этапе. Также были сформулированы выводы и завершено оформление педагогического проекта Пути решенияДля проверки гипотезы были намечены пути решения проблем через

• 
  Использование в процессе обучения прикладных задач;
  
• 
  Выполнение практических и лабораторных работ;
  
• 
  Разработка и проведение интегрированных уроков, практикумов, семинаров и т.д.;
  
• 
  Использование современных педагогических технологий: ИКТ, метод проектов, проблемное обучение модельный метод обучения (занятия в виде деловых игр и др.)
  
• 
  Подготовка сообщений о методах использования математического аппарата в разных науках и в производственной сфере
  

Следует отметить, что повышение эффективности уроков и уровня познавательной активности невозможно без различных видов и форм внеурочной деятельности, таких как олимпиады, конкурсы, предметные декады, проектная деятельность, экскурсии.В работе над проблемой исследования использовались информационно-коммуникативные технологии.Результативность:В результате

• 
  Проанализировано состояние проблемы исследования в психолого – педагогической и научно – методической литературе.
  
• 
  Экспериментально проверены результаты внедрения в курс математики практико-ориентированных задач.
  
• 
  Разработаны дидактические материалы для учебного процесса и внеурочной работы с применением практических задач
  
• 
  Совместно со студентами разработаны проекты:
  

---

Смотрите также файлы

• Предприятия.docx

• 1. Сыну крсеткіші 1,5 алыдыы 0,5 мм шыны пластинкада толын зындыы 0,5 мкм анша толын орналасады.docx

• Формы и системы оплаты труда на современном предприятии.rtf

• Ким. Егэ. Религия. Наука. Искусство. Задание 1 (4) Члены Клуба любителей древностей.docx

• Принципы составления годового бухгалтерского отчета.docx