ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2 + х22 → mах,
х1 + х2 =6,
х1 ≥ 0, х2 ≥ 0.
Наибольшее значение целевой функции F(х1, х2) …
равно 36
равно 18
равно 72
не достижимо (+ )
16. Задана задача нелинейного программирования
F(х1, х2)= х12 + х22 → min,
х1 + х2 =6,
х1 ≥ 0, х2 ≥ 0.
Наименьшее значение целевой функции F(х1, х2) …
равно 18
равно 36
равно 6
равно 9
17. Задана задача нелинейного программирования
F(х1, х2)= х12 + х22 → mах,
х1 + х2 =6,
х1, х2 - любые.
Наибольшее значение целевой функции F(х1, х2) …
не достижимо (+ )
равно 36
равно 18
равно 72
18. Задана задача нелинейного программирования
F(х1, х2)= х12 + х22 → min,
х1 + х2 =6,
х1, х2 - любые.
Наименьшее значение целевой функции F(х1, х2) …
равно 18
равно 36
равно 6
равно 9
равно 0
не достижимо (- )
19. Область допустимых решений задачи нелинейного программирования имеет вид:
Тогда максимальное значение функции F(х1, х2)= х12 +х22 равно…
36
72
25
12
20. Область допустимых решений задачи нелинейного программирования имеет вид:
Тогда минимальное значение функции F(х1, х2)= х12 +х22 равно…
0
6
9
16
Вариант 3
1. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Тогда верно утверждение…
2 + 2 = 1
+ = 0
2. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = = v, то число v называется …
ценой игры
точкой равновесия
оптимальной стратегией
смешанной стратегией
3. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = , то игра называется…
игрой с седловой точкой
неразрешимым конфликтом
игрой без правил
4. Вектор, каждая из компонент которого показывает относительную частоту использования
игроком соответствующей чистой стратегии, называется…
смешенной стратегией
направляющим вектором
вектором нормали
градиентом
5. Симплекс-метод - это:
аналитический метод решения основной задачи линейного программирования
метод отыскания области допустимых решений задачи линейного программирования;
графический метод решения основной задачи линейного программирования;
метод приведения общей задачи линейного программирования к каноническому виду.
6. Задача линейного программирования состоит в:
отыскании наибольшего или наименьшего значения линейной функции при наличии линейных ограничений
разработке линейного алгоритма и реализации его на компьютере
составлении и решении системы линейных уравнений
поиске линейной траектории развития процесса, описываемого заданной системой ограничений.
7. Область допустимых решений задачи линейного программирования не может выглядеть так:
8. Целевой функцией задачи линейного программирования может являться функция:
F=12x1+20x2–30x3 →min
F=
→min
F=
→max
F=
→max.
9. Для решения транспортной задачи может применяться…
метод потенциалов
метод множителей Лагранжа
метод Гаусса
метод дезориентации
10. В системе ограничений общей задачи линейного программирования …
могут присутствовать и уравнения, и неравенства
могут присутствовать только уравнения
могут присутствовать только неравенства
11. В системе ограничений стандартной (симметричной) задачи линейного программирования …
могут присутствовать только неравенства
могут присутствовать и уравнения, и неравенства
могут присутствовать только уравнения
12. В системе ограничений канонической (основной) задачи линейного программирования …
могут присутствовать только уравнения (при условии неотрицательности переменных)
могут присутствовать только неравенства (при условии неотрицательности переменных)
могут присутствовать и уравнения, и неравенства (при условии неотрицательности переменных)
13. При решении задач целочисленного программирования может применяться …
метод Гомори
метод множителей Лагранжа
метод Гаусса
метод аппроксимации Фогеля
14. В основе решения задач методом динамического программирования лежит…
принцип оптимальности Беллмана
принцип «бритва Оккама»
принцип «зуб - за зуб, око- за око»
принцип Гейзенберга
15. Нижняя цена матричной игры, заданной платежной матрицей
, …
меньше верхней цены
равна верхней цене
не существует
16. Верхняя цена матричной игры, заданной платежной матрицей , …
Больше нижней цены
равна нижней цене
не существует
17. Матричная игра, заданная платежной матрицей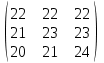
, …
имеет седловую точку
не имеет седловой точки
не является парной
18. Цена игры, заданной платежной матрицей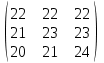 , равна…
22
21
20
23
24
19. Матричная игра, заданная платежной матрицей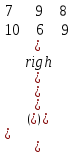
, …
является парной
имеет седловую точку
не является парной
20. Парная игра с нулевой суммой, заданная своей платежной матрицей, может быть сведена к …
задаче линейного программирования
задаче нелинейного программирования
целочисленной задаче линейного программирования
классической задаче оптимизации
х1 + х2 =6,
х1 ≥ 0, х2 ≥ 0.
Наибольшее значение целевой функции F(х1, х2) …
равно 36
равно 18
равно 72
не достижимо (+ )
16. Задана задача нелинейного программирования
F(х1, х2)= х12 + х22 → min,
х1 + х2 =6,
х1 ≥ 0, х2 ≥ 0.
Наименьшее значение целевой функции F(х1, х2) …
равно 18
равно 36
равно 6
равно 9
17. Задана задача нелинейного программирования
F(х1, х2)= х12 + х22 → mах,
х1 + х2 =6,
х1, х2 - любые.
Наибольшее значение целевой функции F(х1, х2) …
не достижимо (+ )
равно 36
равно 18
равно 72
18. Задана задача нелинейного программирования
F(х1, х2)= х12 + х22 → min,
х1 + х2 =6,
х1, х2 - любые.
Наименьшее значение целевой функции F(х1, х2) …
равно 18
равно 36
равно 6
равно 9
равно 0
не достижимо (- )
19. Область допустимых решений задачи нелинейного программирования имеет вид:
Тогда максимальное значение функции F(х1, х2)= х12 +х22 равно…
36
72
25
12
20. Область допустимых решений задачи нелинейного программирования имеет вид:
Тогда минимальное значение функции F(х1, х2)= х12 +х22 равно…
0
6
9
16
Вариант 3
1. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Тогда верно утверждение…
2 + 2 = 1
+ = 0
2. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = = v, то число v называется …
ценой игры
точкой равновесия
оптимальной стратегией
смешанной стратегией
3. Пусть - нижняя цена, а - верхняя цена парной игры с нулевой суммой. Если = , то игра называется…
игрой с седловой точкой
неразрешимым конфликтом
игрой без правил
4. Вектор, каждая из компонент которого показывает относительную частоту использования
игроком соответствующей чистой стратегии, называется…
смешенной стратегией
направляющим вектором
вектором нормали
градиентом
5. Симплекс-метод - это:
аналитический метод решения основной задачи линейного программирования
метод отыскания области допустимых решений задачи линейного программирования;
графический метод решения основной задачи линейного программирования;
метод приведения общей задачи линейного программирования к каноническому виду.
6. Задача линейного программирования состоит в:
отыскании наибольшего или наименьшего значения линейной функции при наличии линейных ограничений
разработке линейного алгоритма и реализации его на компьютере
составлении и решении системы линейных уравнений
поиске линейной траектории развития процесса, описываемого заданной системой ограничений.
7. Область допустимых решений задачи линейного программирования не может выглядеть так:
8. Целевой функцией задачи линейного программирования может являться функция:
F=12x1+20x2–30x3 →min
F=
→minF=
→maxF=
→max.9. Для решения транспортной задачи может применяться…
метод потенциалов
метод множителей Лагранжа
метод Гаусса
метод дезориентации
10. В системе ограничений общей задачи линейного программирования …
могут присутствовать и уравнения, и неравенства
могут присутствовать только уравнения
могут присутствовать только неравенства
11. В системе ограничений стандартной (симметричной) задачи линейного программирования …
могут присутствовать только неравенства
могут присутствовать и уравнения, и неравенства
могут присутствовать только уравнения
12. В системе ограничений канонической (основной) задачи линейного программирования …
могут присутствовать только уравнения (при условии неотрицательности переменных)
могут присутствовать только неравенства (при условии неотрицательности переменных)
могут присутствовать и уравнения, и неравенства (при условии неотрицательности переменных)
13. При решении задач целочисленного программирования может применяться …
метод Гомори
метод множителей Лагранжа
метод Гаусса
метод аппроксимации Фогеля
14. В основе решения задач методом динамического программирования лежит…
принцип оптимальности Беллмана
принцип «бритва Оккама»
принцип «зуб - за зуб, око- за око»
принцип Гейзенберга
15. Нижняя цена матричной игры, заданной платежной матрицей
, …меньше верхней цены
равна верхней цене
не существует
16. Верхняя цена матричной игры, заданной платежной матрицей
, …Больше нижней цены
равна нижней цене
не существует
17. Матричная игра, заданная платежной матрицей
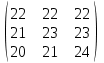, …имеет седловую точку
не имеет седловой точки
не является парной
18. Цена игры, заданной платежной матрицей
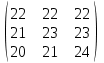, равна…22
21
20
23
24
19. Матричная игра, заданная платежной матрицей
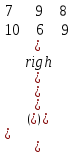, …является парной
имеет седловую точку
не является парной
20. Парная игра с нулевой суммой, заданная своей платежной матрицей, может быть сведена к …
задаче линейного программирования
задаче нелинейного программирования
целочисленной задаче линейного программирования
классической задаче оптимизации