Файл: Урок по теме Логарифмы. Десятичные и натуральные логарифмы. Цели урока Обучающая ввести понятия логарифма, десятичного и натурального логарифма познакомить обучающихся с их применением в различных областях.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
10. ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ»
Потому-то, словно пена,
Отпадают наши рифмы.
И величие степенно
Отступает в логарифмы.
(Б. Слуцкий)
Урок по теме: «Логарифмы. Десятичные и натуральные логарифмы».
Цели урока:
-
Обучающая:
-
ввести понятия логарифма, десятичного и натурального логарифма; познакомить обучающихся с их применением в различных областях; -
способствовать формированию умений вычислять логарифмы.
-
Развивающая:
-
способствовать развитию внимания, математического кругозора, логического мышления, познавательного интереса к дисциплине;
-
способствовать формированию умений применять приемы мыслительной деятельности: сравнения, обобщения, анализировать и делать выводы -
Воспитательная:
-
способствовать воспитанию чувства самостоятельности, аккуратности, культуры поведения, организованности, ответственности за свои действия на уровне компетенций.
Формирование компетенций:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
Методическая цель урока:
-
продемонстрировать приемы активизации мыслительной деятельности на различных этапах урока; -
продемонстрировать применение ИКТ.
Тип урока:
урок изучения нового материала..
Вид урока:
беседа, решение упражнений.
Методы обучения:
-
по источнику познания: словесные, практические, наглядные; -
по характеру познавательной деятельности: фронтальная работа, работа в группах, элементы кейс-метода.
План урока.
-
Организационный этап. Постановка цели и задач урока. Мотивация учебной деятельности обучающихся. (2 мин). -
Актуализация опорных знаний (задание на внимание).(5 мин). -
Формирование новых понятий и способов действий. (13 мин). -
Формирование навыков умственного труда (22 мин). -
Информация о домашнем задании, инструктаж по его выполнению.
(1 мин).
-
Рефлексия (подведение итогов занятия) и выставление оценок (2 мин).
Оснащение урока.
-
Технические средства: интерактивная доска. -
Дидактические средства: презентация по теме: «Логарифмы», раздаточный материал. -
Логарифмическая линейка.
Ход урока.
І. Организационный момент. (2 мин).
Проводится преподавателем с целью установления дисциплины, общей готовности к уроку, концентрации внимания, психологического настроя обучающихся на урок;
Преподаватель: Сегодня на уроке мы познакомимся с новыми для вас понятиями «логарифм», «десятичный логарифм» и «натуральный логарифм», познакомимся с некоторыми способами их вычисления.
ІІ.Актуализация опорных знаний (5мин.)
Устный счет:
1. Вычислить:
; 
; 
; 
; 
; 
; 
; 
; 
; 
;
;
; 
;
; 
; 
; 
;
; 
; 42; 
; 
.2. Решите уравнения:
-
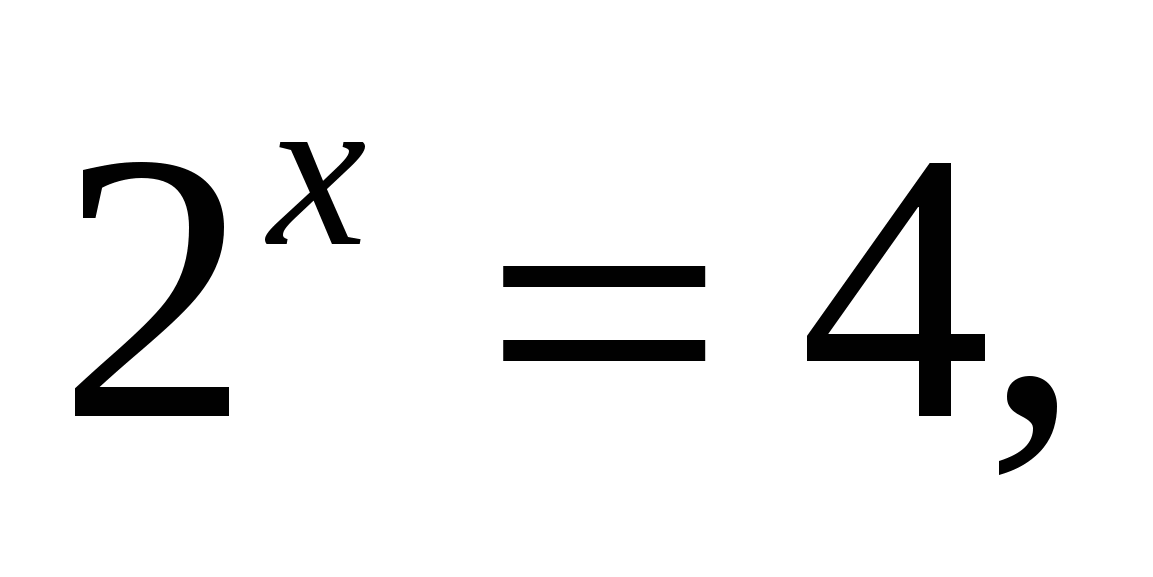(ответ: 2); -
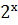= 2, (ответ: 1) - 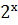= 1, (ответ: 0)
- =
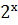, (ответ: -1) -
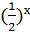= 1, (ответ: 0) - 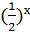= 2, (ответ: -1)
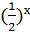- = 8, (ответ: -3)
-
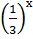= 27, ( ответ: -3); - 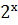= 0, (ответ: корней нет)
-
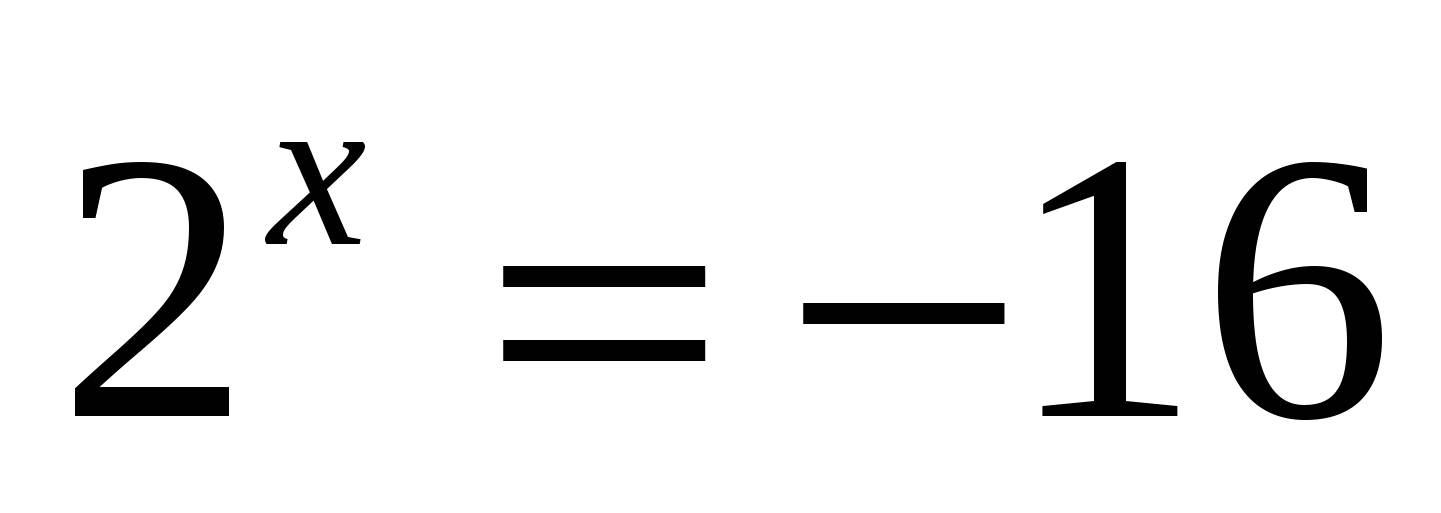( ответ: корней нет); -
.
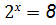
ІІІ. Формирование новых понятий и способов действий (13мин.)
Начнем новую тему с определения.
Опр. Логарифмом положительного числа в по основанию а, причем а>0 и а≠1, называется показатель степени
х, в которую надо возвести число а, чтобы получить число в.
Записываем следующим образом:
= х, следовательно 
= в.Акцентирую ваше внимание на том, что под знаком логарифма и в основании логарифма по определению может стоять только положительное число, причем в основании еще и не равное единице. Другие варианты мы рассматривать не будем.
Приведем примеры: (слайд презентации, преподаватель комментирует каждый пример).
=3, так как 
=8; 
=3, так как 
=27; 
= 0, так как 
=1 
= -1, так как 
=
= 
, так как 
= 
В тетрадь записать один из понравившихся на выбор примеров.
Логарифм – это операция, обратная возведению в степень.
Кроме обычных логарифмов существуют еще десятичные и натуральные логарифмы.
Опр. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо
.
Примеры: (слайд презентации, преподаватель комментирует каждый пример).
-
lg10=1; -
lg100=2; -
lg1=0; -
lg0,1=-1; -
lg0,01=-2.
В тетрадь записать один из понравившихся на выбор примеров.
Опр. Натуральным логарифмом числа называют логарифм этого числа по основанию е, где е – иррациональное число, приближенно равное 2,7. При этом пишут ln b вместо
.Число е - математическая константа. Иногда его называют числом Эйлера (Леонард Эйлер - швейцарский, немецкий и российский математик, ввел обозначение е в 1736 году и вычислил первые 23 знака этого числа) или числом Непера (В 1614 году шотландский математик ДЖОН НЕПЕР изобрёл таблицы логарифмов. Принцип их заключался в том, что каждому числу соответствует специальное число-логарифм. Логарифмы очень упрощают вычисления. В дальнейшем им была изобретена логарифмическая линейка-верная спутница в математических расчетах всех инженеров и учёных до 70-х годов ХХ столетия. Впервые число е Непер упоминает в одной из своих работ в 1618 году, но тогда она обозначалась другой буквой, буквой b).
Саму же константу впервые вычислил швейцарский математик Якоб Бернулли. Букву {\displaystyle e}е начал использовать Эйлер в 1727 году. Первые 1000 знаков после запятой в числе е выглядят так: 2,7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260 5956307381 3232862794 3490763233 8298807531 9525101901 1573834187 9307021540 8914993488 4167509244 7614606680 8226480016 8477411853 7423454424 3710753907 7744992069 5517027618 3860626133 1384583000 7520449338 2656029760 6737113200 7093287091 2744374704 7230696977 2093101416 9283681902 5515108657 4637721112 5238978442 5056953696 7707854499 6996794686 4454905987 9316368892 3009879312 7736178215 4249992295 7635148220 8269895193 6680331825 2886939849 6465105820 9392398294 8879332036 2509443117 3012381970 6841614039 7019837679 3206832823 7646480429 5311802328 7825098194 5581530175 6717361332 0698112509 9618188159 3041690351 5988885193 4580727386 6738589422 8792284998 9208680582 5749279610 4841984443 6346324496 8487560233 6248270419 7862320900 2160990235 3043699418 4914631409 3431738143 6405462531 5209618369 0888707016 7683964243 7814059271 4563549061 3031072085 1038375051 0115747704 1718986106 8739696552 1267154688 9570350354.
математический смысл числа е:
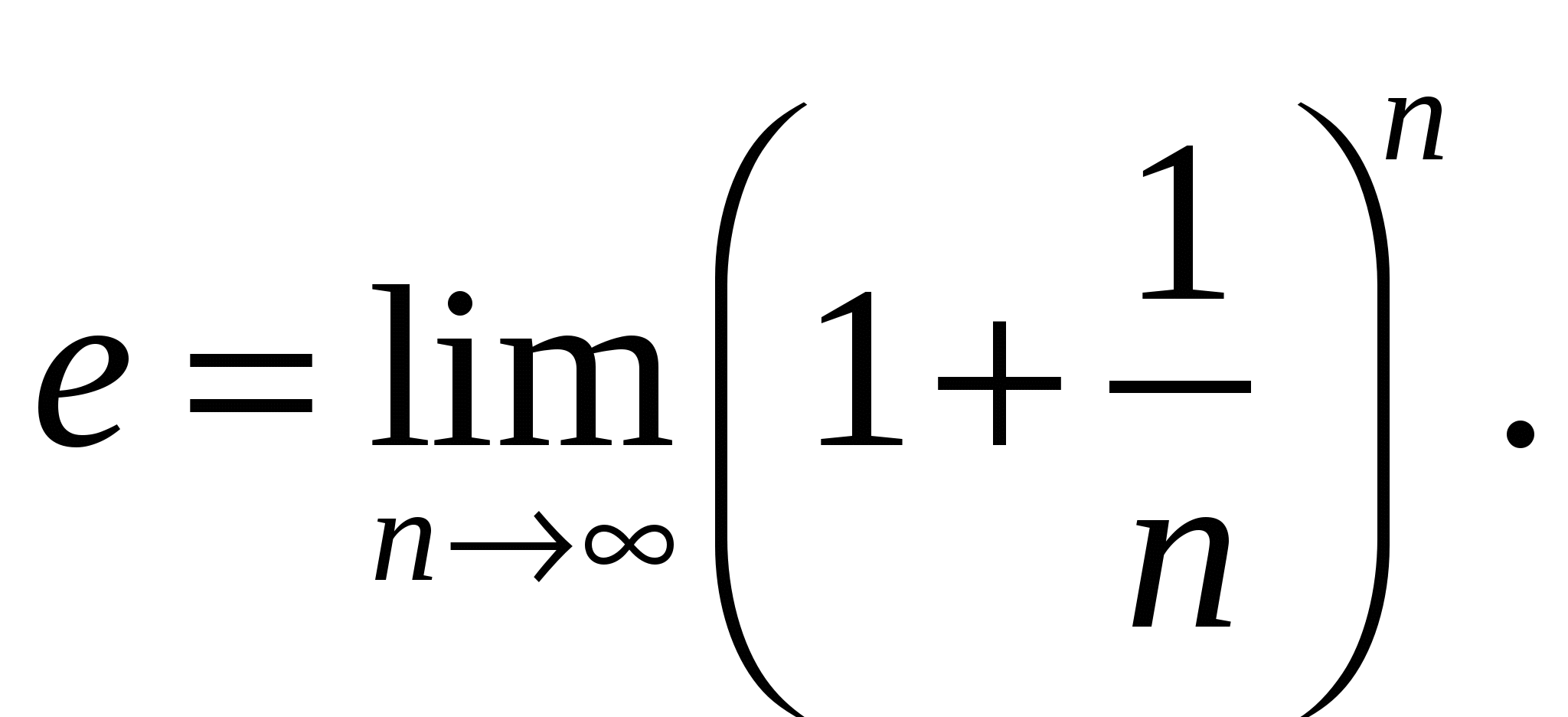(это первый замечательный предел).Примеры: (слайд презентации, преподаватель комментирует каждый пример).