ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 82
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема - Логические приемы составления и анализа релейно-контактных схем
Тип урока – Лабораторно практическая работа
Цель работы:
Исследовать применение релейно-контактных схем при решении профессиональных и жизненных ситуаций с помощью обращения к булевым функциям.
Задачи:
Образовательная: исследование применения релейно-контактных схем при решении профессиональных и жизненных ситуаций с помощью обращения к булевым функциям.
Воспитательная: воспитание дисциплинированности, аккуратности, самостоятельности в работе, формировать ответственность за конечный результат и интерес к предмету
Развивающая: развитие мышления, внимания; развитие познавательных интересов в области информатизации, расширять кругозор
Структура урока:
-
Организационный момент (Проверка присутствующих. Сообщение темы и цели урока) -
Повторение изученного материала – Прочитать Методические указания к заданию
Дополнительные источники информации:
https://www.youtube.com/watch?v=fGG5H4nRays - Релейно-контактные схемы и двоичные функции
http://electrik.info/main/school/235-buleva-algebra-chast-3-kontaktnye-sxemy.html - Булева алгебра. Часть 3. Контактные схемы
https://ppt-online.org/368949 - Релейно-контактные схемы
-
САМОСТОЯТЕЛЬНОЕ ЗАДАНИЕ -
ЗАДАНИЕ 1
Упростить заданную функцию и Составить релейно-контактные схемы по заданной функции и упрощенной функции. (2 схемы должно быть)
ЗАДАНИЕ 2
Составьте алгебраическое выражение для мостиковой схемы, приведенной ниже.
-
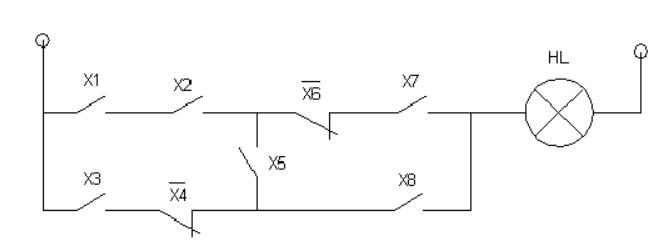
Подведение итогов, оценка работ.
ПРИМЕЧАНИЕ:
В зависимости от качества и количества заданий, выполнения работы - она будет оцениваться до 10 баллов.
Методические указания к заданию
Современные системы автоматизации производственных процессов часто требуют построения цепей, где реализуется достаточно сложная логика преобразования дискретных входных сигналов в выходные дискретные. Традиционно такое логическое преобразование осуществлялось с помощью релейно-контактных элементов. Однако в последнее время такое преобразование осуществляется с помощью дискретных логических компонентов транзисторных переключательных схем, реализующих те или иные логические функции.
Поэтому на данный момент наиболее актуальна проблема анализа и синтеза релейно-контактных схем при проектировании различных электронных приборов. Из этого можно сделать вывод, что методы логического анализа и синтеза релейно-контактных схем находят широкое применение в разных бытовых жизненных ситуациях.
В теории релейно-контактных схем важнейшим являются следующие задачи:
— задача синтеза релейно-контактных схем — это составление релейно-контактных схем с заданными условиями работы, которые зависят от функций, которые эта схема должна выполнять;
— задача анализа релейно-контактных схем — это получение наиболее простой схемы, реализующей данную формулу.
Релейно-контактной схемой называется устройство из проводников и двухпозиционных контактов, через которые полюсы источника тока связаны с некоторым потребителем. Контакты могут быть замыкающими и размыкающими. Каждый контакт подключен к некоторому реле (переключателю). Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие контакты разомкнуты; в противном случае — наоборот. Каждому реле ставится в соответствие своя пропозициональная переменная х Она принимает значение 1, если через реле проходит ток, и 0 в противном случае. На чертежах все замыкающие контакты, подключенные к реле х, обозначаются символом
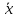, а размыкающие — символом х. Это означает, что при срабатывании реле х все его размыкающие контакты х не проводят ток и им сопоставляется 0. При отключении реле создастся противоположная ситуация. Всей схеме также ставится в соответствие булева переменная у, которая равна 1, если схема проводит ток, и 0 в противном случае. Переменная
у, соответствующая схеме, очевидно, является булевой функцией от переменных Хп соответствующих реле. Эта функция называется функцией проводимости схемы, а ее таблица — условиями работы схемы.
Таблица истинности - это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
К числу таких логических элементов относятся:
• элемент инвертирования (отрицание, НЕ, NOT) входного дискретного сигнала, эквивалентный размыкающему контакту (рис1 а).
• элемент конъюнкции (логического умножения, И, AND) двух входных дискретных сигналов, эквивалентный последовательному соединению (рис 1 б).
• элемент дизъюнкции (логического сложения, ИЛИ, OR) двух входных дискретных сигналов, эквивалентный параллельному соединению (рис1 в).
Любую схему можно задать формулой алгебры логики, при этом конъюнкции двух высказываний соответствует последовательное соединение двух переключателей, а дизъюнкции двух высказываний — параллельное соединение двух переключателей. При этом ток будет проходить через данные схемы тогда и только тогда, когда истинностное значение соответствующей формулы — «истина». А аналогом инверсии – нормально замкнутый контакт
Рис 1. Контактные аналоги логических функций
При анализе и синтезе релейно-контактных схем пользуются аналитической записью работы как всей схемы, так и ее отдельных элементов. При этом различные вспомогательные элементы схем (трансформаторы и выпрямители для питания цепей управления, защитные аппараты – плавкие предохранители, тепловые реле, клеммы, разъемы и т. д.), непосредственно не участвующие в создании логики схемы, в запись не вводятся. После получения структуры схемы такие элементы вводятся в нее, чтобы защитить отдельные цепи и механизмы и сделать обслуживание удобным и безопасным. Силовые цепи механизмов также не вводятся в аналитическую запись.
Теперь перейдем непосредственно к решению практических задач на применение булевых функций к релейно-контактным схемам.
Задача № 1. Составить схему, позволяющую включать и выключать свет в вашей комнате любым из трех различных выключателей. Выключатели расположены у входа в комнату, над постелью и у письменного стола.
Используя условия, которым должна удовлетворять искомая схема, составим сначала таблицу значений функции проводимости F этой схемы. В нее войдут три неизвестных х, у, г, которые будут соответствовать трем выключателям. В последнем столбце таблицы, будем указывать 1, если свет горит и 0, если света нет. Рассмотрим набор переменных (0,0,0) (все выключатели в положении «выключен»), свет в этот момент также не горит — значение функции проводимости F будет равно 0. При наборе переменных (1,1,1 )(все выключатели в положении «включен»), свет в этот момент горит — значение функции проводимости F будет равно 1. По условию задачи, при изменении положения любого из выключателей должен загореться свет, то есть на наборах (1,0,0), (0,1,0) и (0,0,1) функция F равна 1. При следующем изменении положения любого из выключателей свет должен выключиться, то есть на наборах (1,1,0), (1,0,1) и (0,1,1) функция F равна 0 (табл. 1).
Таблица 1 – Таблица истинности
| X | У | Z | F |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
Зная теперь вес наборы значений аргумента, на которых функция F обращается в 1, запишем выражение для нее, используя алгоритм приведения функции к совершенной дизъюнктивной нормальной форме по таблице истинности, а уже затем упростим его:
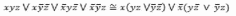
Изображаем релейно-контактную схему, обладающую найденной функцией проводимости (рис. 2).
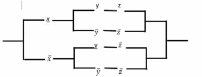
Рис 2. Релейно-контактная схема
Алгебра логики и базирующаяся на ней алгебра релейных схем пользуются законами, во многом напоминающими законы обычной алгебры.
Так, для алгебры релейных схем справедливы переместительный и сочетательный законы, а также распределительный закон умножения относительно сложения
1. Переместительный закон:
xy = yx – для логического умножения (рис. 3, а);
x + y = y + x – для логического сложения (рис. 3, б).
2. Сочетательный закон:
(x y)z = x(yz) – для логического умножения (рис. 3, в);
(x + y) + z = x + (y + z) – для логического сложения (рис. 3, г).
3. Распределительный закон умножения относительно сложения:
x(y + z) = xy + xz (рис. 3, д).
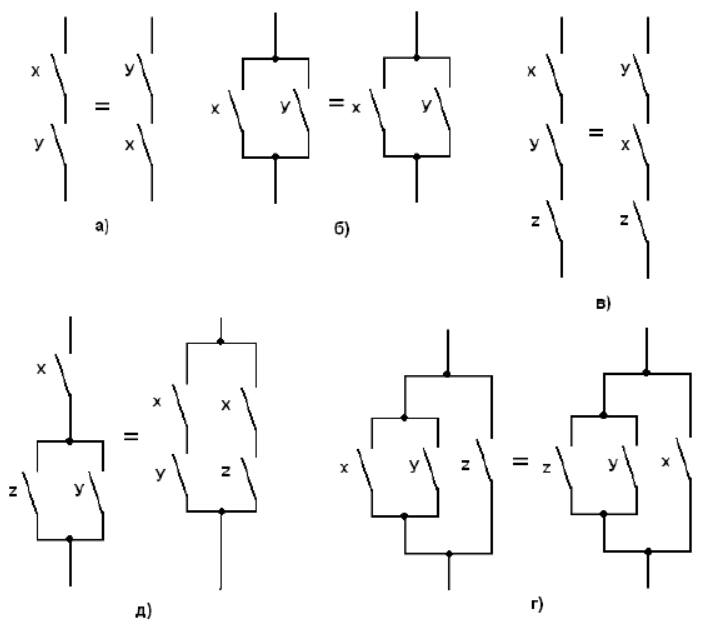
Рис. 3. Графическая интерпретация основных законов алгебры логики
Кроме законов, совпадающих с законами обычной алгебры, алгебра релейных схем имеет собственные законы (рис. 4).
1. Распределительный закон сложения относительно умножения:
x + yz = (x + y) (x + z) (рис. 4, а).
Он является обратным для распределительного закона умножения относительно сложения и получается из последнего путем замены всех знаков на противоположные.
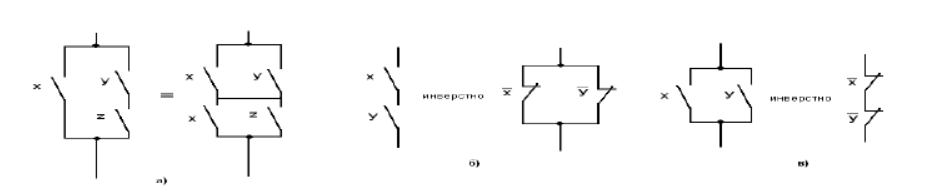
Рис. 4. Графическая интерпретация законов алгебры логики, не имеющих
аналогов в «обычной» алгебре
Действительно, перемножив почленно скобки в правой части, получим:
(x + y) (x + z) = xx + xy + xz + yz = x + xy + xz + yz = x(1 + y + z) + yz = x + yz.
2. Закон повторения:
x*x*x…= x; x + x +…= x.
В этом случае цепь, состоящая из последовательного и параллельного соединения одинаковых контактов одного и того же релейного элемента, равносильна по своему действию одному контакту этого элемента.