ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 83
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Закон инверсии:
– для логического умножения (рис. 4, б); 
– для логического сложения (рис. 4, в). В соответствии с этим законом исходная и инверсная схемы связаны между собой так, что, когда исходная схема представляет собой замкнутую цепь, инверсная схема разомкнута, и наоборот. Следовательно, если исходная схема является постоянно замкнутой (равной единице) цепью, то инверсная ей схема – постоянно разомкнутой (равной нолю). При инвертировании меняются на противоположные не только контакты, но и знаки логических действий. Так, логическое умножение меняется на логическое
сложение, а логическое сложение – на логическое умножение.
Инверсией единицы является ноль, а инверсией ноля – единица:
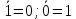
Используя различные сочетания контактов с единицей и нолем, можно получить следующие соотношения:
ПРИЛОЖЕНИЕ
Таблица 1 – Законы алгебры логики для логических элементов
| Закон | Для ИЛИ | Для И |
| Переместительный |  |  |
| Сочетательный |  |  |
| Распределительный |  |  |
| Правила де Моргана |  |  |
| Идемпотенции |  |  |
| Поглощения |  |  |
| Склеивания |  |  |
| Операция переменной с ее инверсией |  |  |
| Операция с константами |  |  |
| Двойного отрицания |  | |