Файл: Вариант 18 в задачах 19 найти общие решения уравнений и частные решения, если есть начальные условия. 1.doc
Добавлен: 30.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Точка 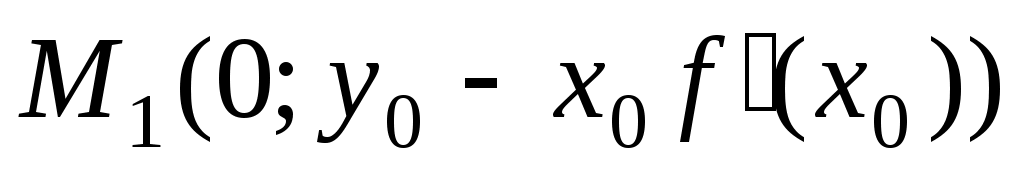 является точкой пересечения оси ОY. По условию задачи длина отрезка
является точкой пересечения оси ОY. По условию задачи длина отрезка 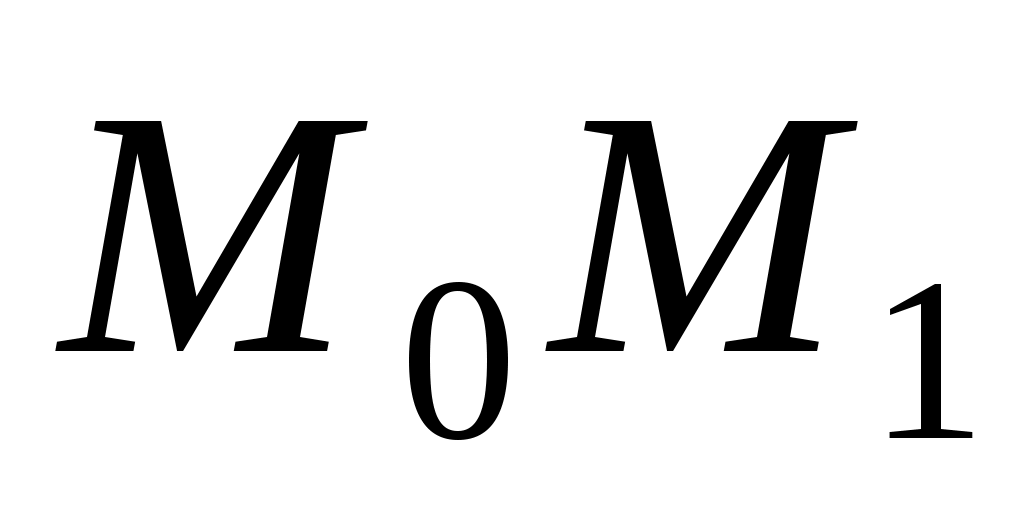 равна 2, т.е.
равна 2, т.е. 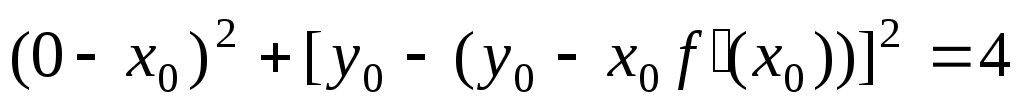 . Или
. Или 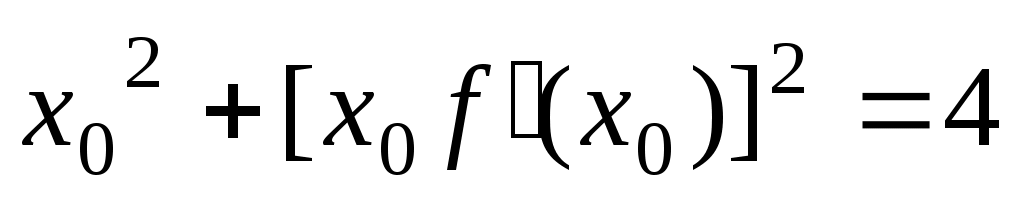 . Это равенство справедливо для любой точки
. Это равенство справедливо для любой точки 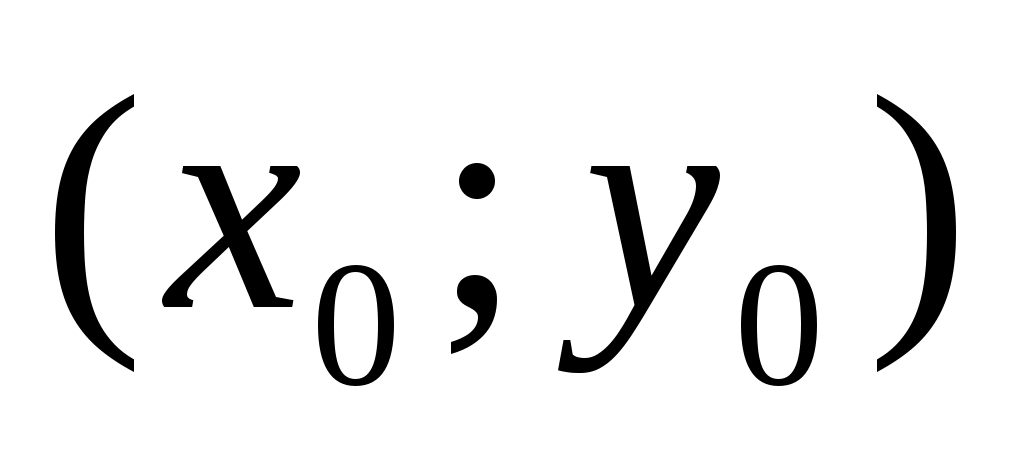 . Заменим эту точку произвольной точкой
. Заменим эту точку произвольной точкой 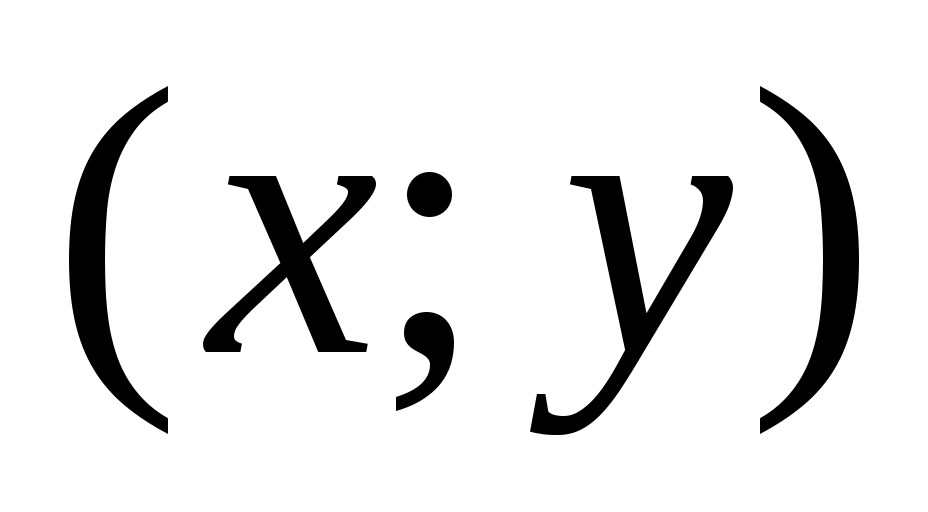 , лежащей на кривой
, лежащей на кривой  . Получим:
. Получим: 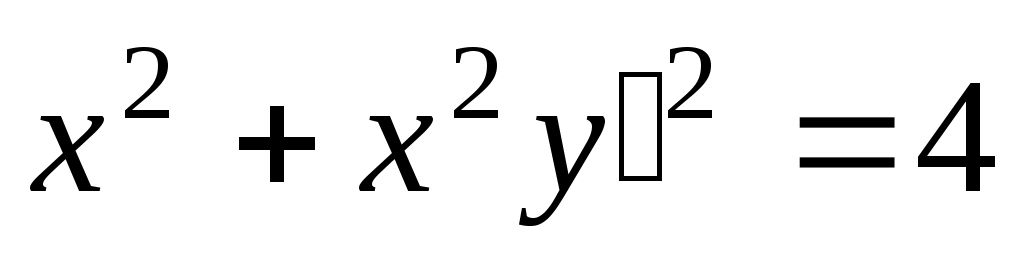 , или
, или 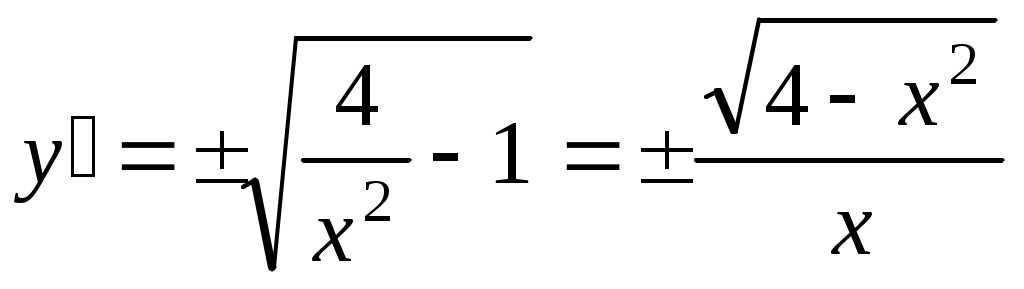 . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем: 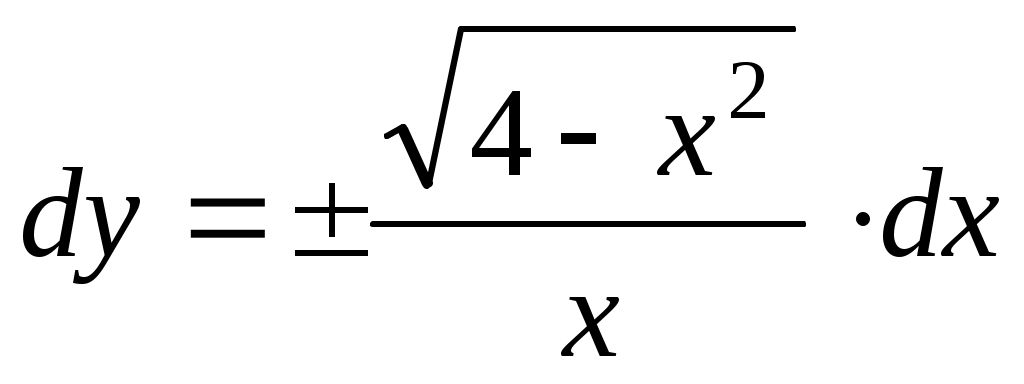 . Интегрируем:
. Интегрируем: 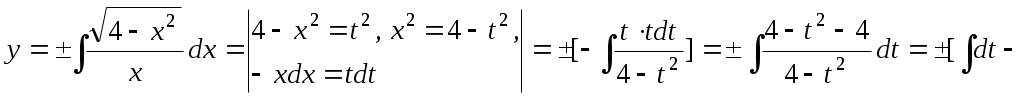
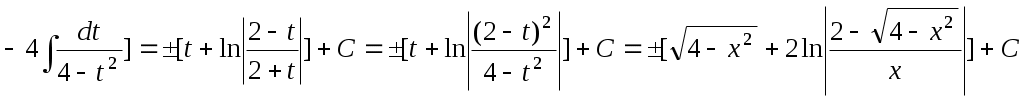 . Находим C, учитывая, что кривая проходит через точку М(2, 0):
. Находим C, учитывая, что кривая проходит через точку М(2, 0): 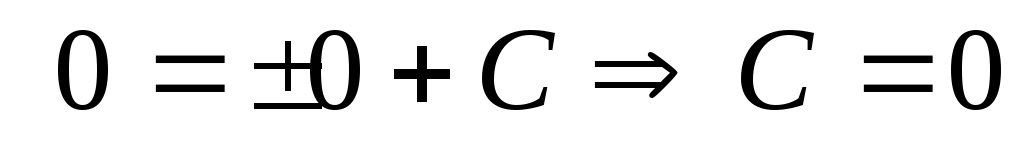 . Тогда
. Тогда 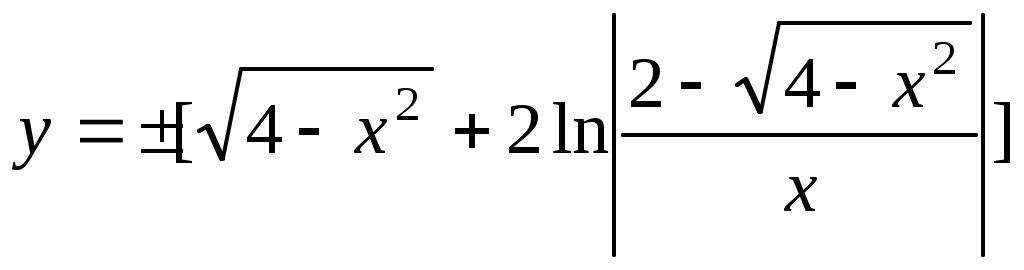 . Ответ:
. Ответ: 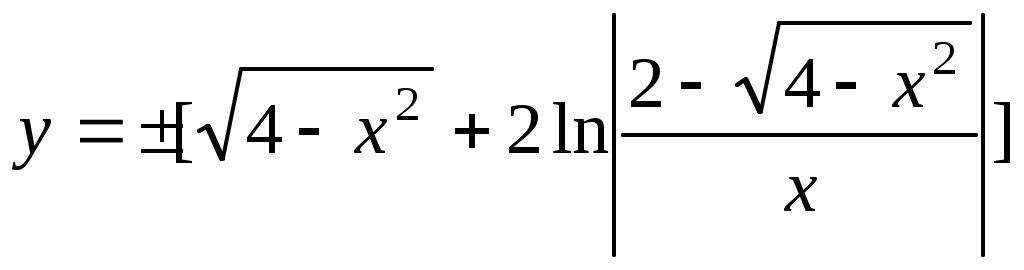 .
.
Пусть масса одного погонного метра цепи равна m. Обозначим через x(t) длину части цепи, свешивающейся со стола в момент времени t после начала скольжения. По условию задачи x(0)=1. К центру тяжести цепи приложена сила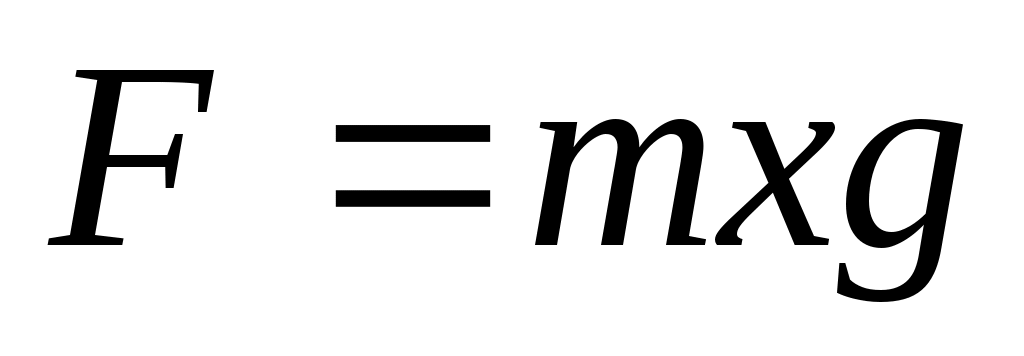 . Масса всей цепи равна 6m. По второму закону Ньютона получаем:
. Масса всей цепи равна 6m. По второму закону Ньютона получаем: 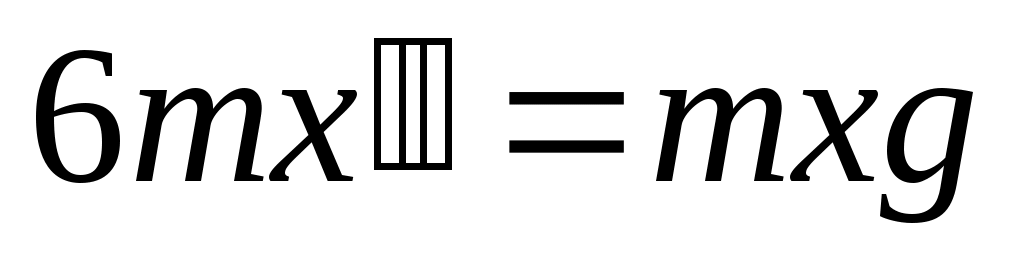 или
или 
. Характеристическое уравнение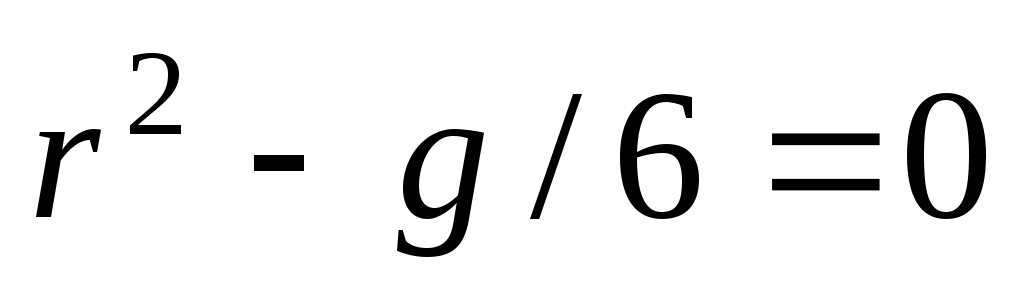 имеет два корня:
имеет два корня: 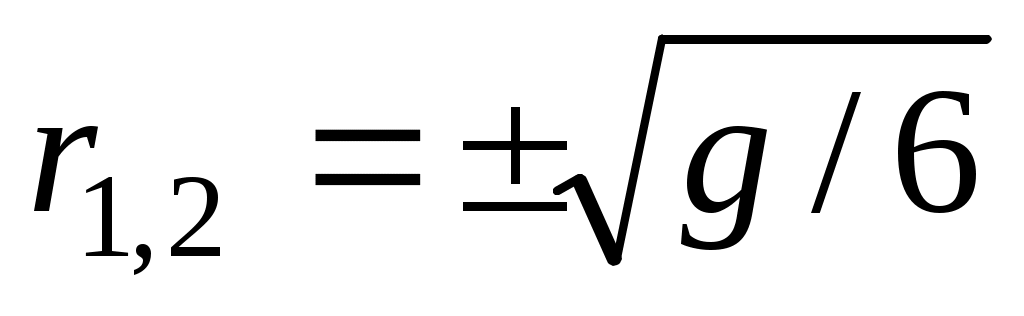 . Следовательно,
. Следовательно, 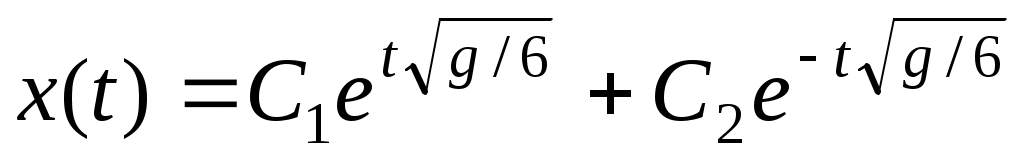 . Для определения частного решения воспользуемся начальными условиями:
. Для определения частного решения воспользуемся начальными условиями: 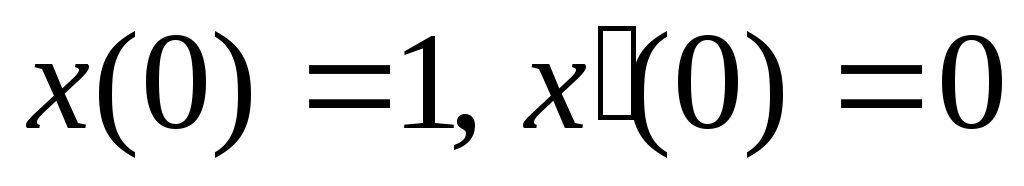 . Получаем
. Получаем 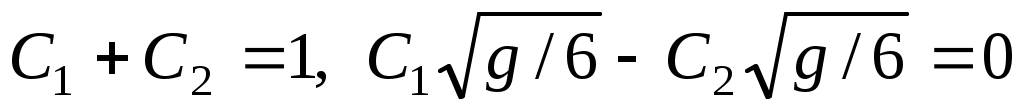 , т.е.
, т.е. 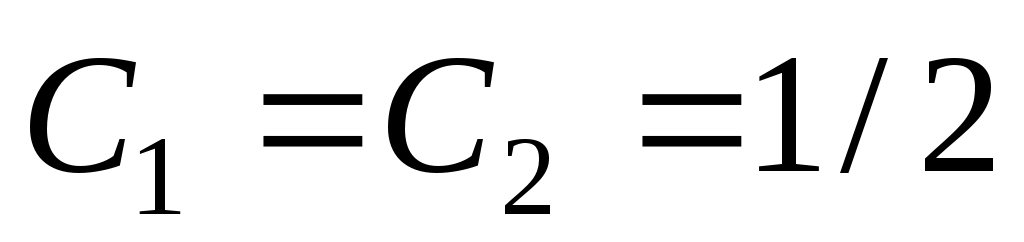 . Тогда частным решением будет функция
. Тогда частным решением будет функция 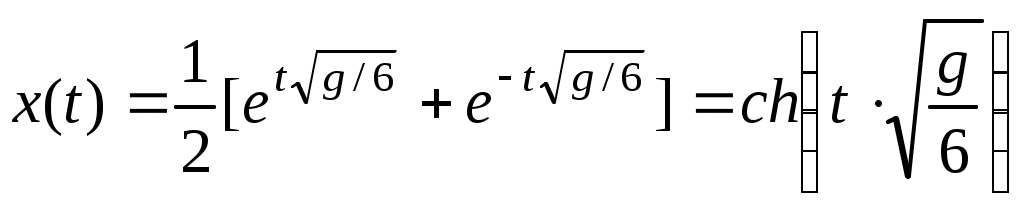 . Разрешим это равенство относительно t:
. Разрешим это равенство относительно t:  . По смыслу переменных следует выбрать знак «+». Окончательно,
. По смыслу переменных следует выбрать знак «+». Окончательно,  . Положим
. Положим 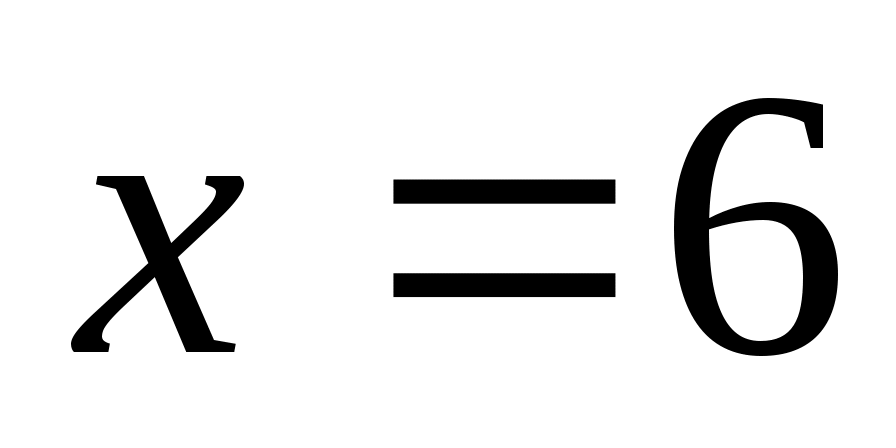 . Получим:
. Получим: 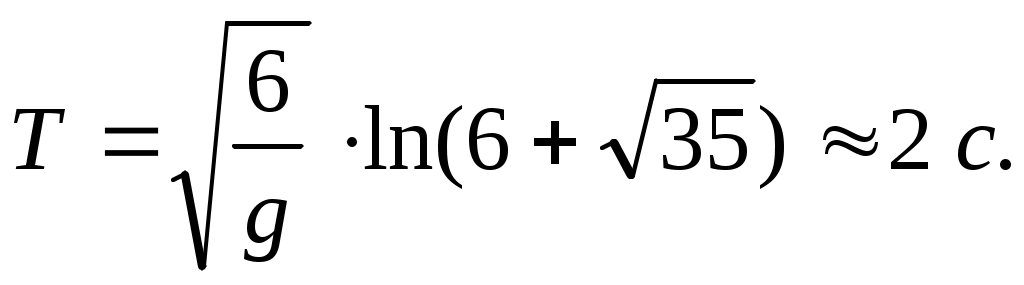 Ответ:
Ответ: 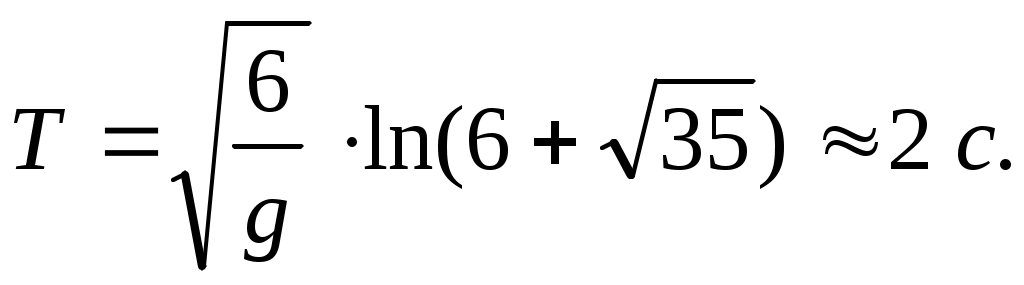
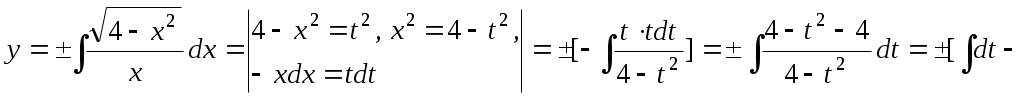
-
Цепь длиной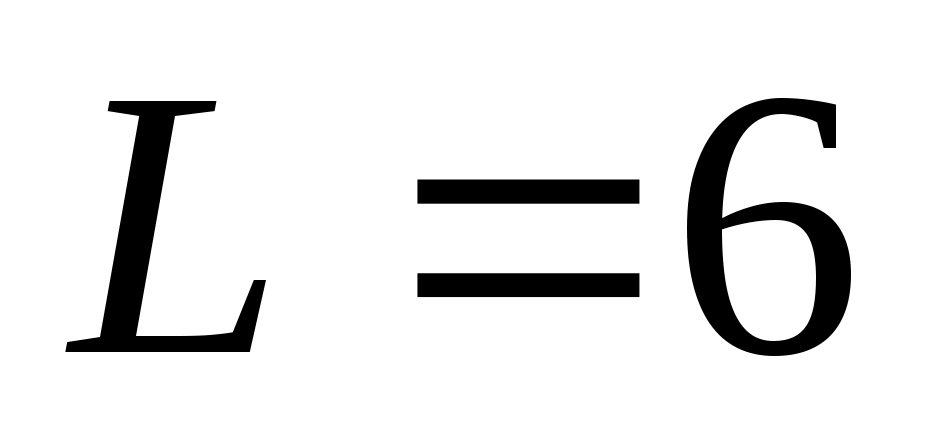 м соскальзывает вниз со стола без трения. В начальный момент свешивался конец цепи длиной
м соскальзывает вниз со стола без трения. В начальный момент свешивался конец цепи длиной 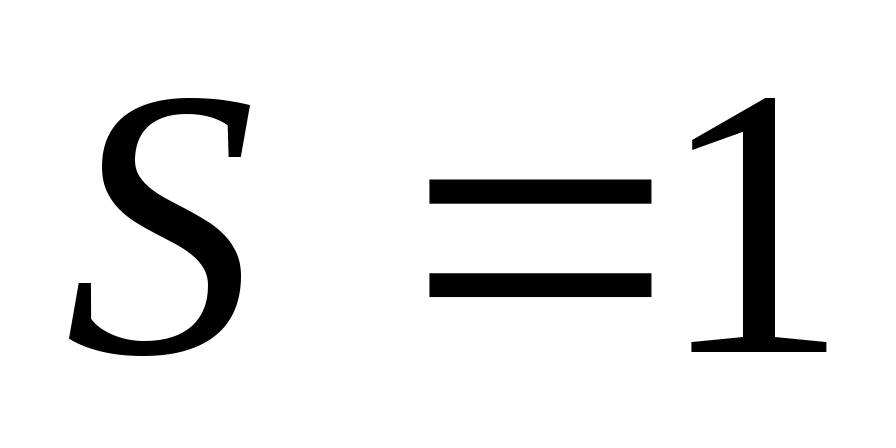 м. Определите время соскальзывания цепи со стола.
м. Определите время соскальзывания цепи со стола.
Пусть масса одного погонного метра цепи равна m. Обозначим через x(t) длину части цепи, свешивающейся со стола в момент времени t после начала скольжения. По условию задачи x(0)=1. К центру тяжести цепи приложена сила
. Характеристическое уравнение