Файл: Исследование характеристик типовых динамических звеньев сау теория автоматического управления Автор учебнометодического пособия Ю. М. Лебедев Томск 2000 Лабораторная работа 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
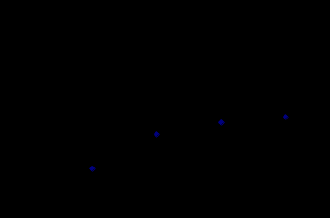
Анализ результатов работы.
Влияние постоянной времени на апериодическое звено:
- при увеличении постоянной времени увеличивается время переходного процесса, уменьшается частота среза, сдвиг фазы не меняется, т.е. запас устойчивости по фазе не зависит от постоянной времени.
Влияние форсирующего звена на инерционное:
- увеличивается время переходного процесса, полоса пропускания частот уменьшается снижается запас устойчивости по фазе.
Влияние коэффициента демпфирования на колебательное звено:
- коэффициент демпфирования колебательного звена увеличивает полосу пропускания частот, время переходного процесса увеличивается, перерегулирование увеличивается, запас устойчивости по фазе снижается.
Ответы на контрольные вопросы:
- Исходя из экспериментальных данных (график, таблица), можно увидеть зависимость tпп =3T, следовательно постоянная времени T инерционного звена пропорционально увеличивается с увеличением времени переходного процесса tпп.
-
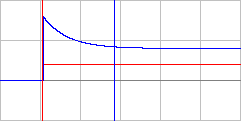Характеристики изменятся следующим образом:в начальный момент будет скачок напряжения, время переходного процесса уменьшится tпп=0,18с.
АЧХ и ФЧХ будут иметь следующий вид:
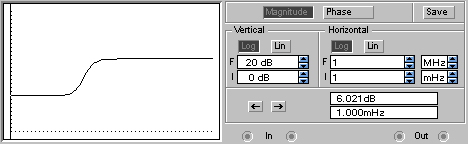
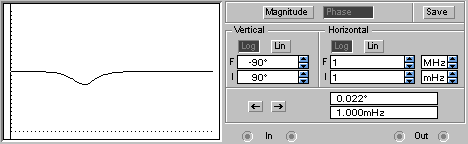
Исчезнет частота среза ωср (т.е. звено будет иметь усилительные свойства на всех частотах). Значение фазы φ сризменяется от близкого к нулю, затем с увеличением АЧХ принимает отрицательное значение, а потом снова близкое к нулю.
- Колебательное звено становится консервативным, когда коэффициент демпфирования равен нулю, колебания переходного процесса становятся незатухающими, амплитуда на сопрягающей частоте становится бесконечной, фаза скачком из 0 становится равной -π.
- Исключив сопротивление R3-обратной связи первого каскада, получим из колебательного звена консервативное.
- Апериодическое звено второго порядка состоит из двух последовательно соединенных апериодических звеньев первого порядка, в связи с этим при суммировании двух экспоненциальных составляющих происходит перегиб.