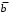ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 92
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
При минимизации следует руководствоваться следующими правилами:
1) Строится и размечается прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов.
2) В клетки таблицы заносятся значения булевой функции. При поиске клеточки таблицы аргумент набора равный 0 берется без отрицания, а равный 1 – с отрицанием. В найденную клетку записывают значение функции.
3) Обводят контурами все 0 с соблюдением следующих правил:
- контур должен быть прямоугольным;
- внутри контура не должно быть единиц;
- при обводке следует получить минимальное число контуров максимальной площади;
- число нулей в контуре должно быть равно степени числа 2 (1, 2, 4, 8, 16,…);
- одна и та же клетка, заполненная нулем может входить в несколько контуров;
- при обводке следует учитывать, что самая верхняя и самая нижняя строки таблицы являются соседними. Соседними являются также крайний левый и крайний правый столбцы.
- количество контуров должно быть как можно меньше, а площадь контуров – как можно больше.
4) Записывают минимальное выражение как функцию Пирса над логическими выражениями, которые описывают контура таблицы. Логическое выражение для контура представляет собой операцию Пирса от аргументов. Для поиска логического выражения для контура выясняют, от каких аргументов он зависит. Если все нули контура приписаны к аргументу
, то в логическое выражение этот аргумент входит. Если все единицы контура помечены инверсией аргумента, то в выражение вписывается 
. Если в контуре есть нули, помеченные и нули, помеченные , то в описание контура этот аргумент не входит.ВАЖНО! При минимизации в базисах Шеффера и Пирса действуют два дополнительных правила:
Если контур занимает половину таблицы, то над аналитическим описанием этого контура ставится дополнительное отрицание;
Если в таблице только один контур, то над ним также следует поставить дополнительное отрицание.
Естественно, если в таблице только один контур, и он занимает половину таблицы, то над ним ставятся два дополнительных отрицания.
Пример: минимизировать в базисе Пирса функции:
 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
, 
, 
, 
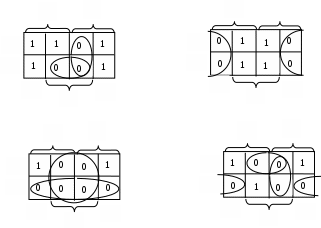
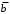
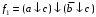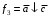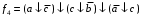.Очевидно Вы заметили, что правила заполнения и обводки одинаковы при минимизации в базисе Пирса и при получении минимальных конъюнктивных нормальных форм. Следовательно, МКНФ можно получить из этих же таблиц:
, 
, 
, 
.
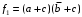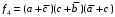
Минимизация булевых функций большого числа аргументов.
Для минимизации булевых функций большого числа аргументов могут быть использованы различные методы: метод неопределенных коэффициентов, метод минимизирующих карт, метод Квайна – Мак-Класки и т.д. Многие из методов страдают громоздкостью записи при их использования, некоторые работают только с полностью определенными булевыми функциями, а большинство методов позволяет получить только минимальные дизъюнктивные нормальные формы.
Рассмотрим идею простейшего метода минимизации функций произвольного числа аргументов, который легко программируется и пригоден для минимизации не полностью определенных булевых функций. Используя эту идею легко получить алгоритмы минимизации булевых функций не только в МДНФ и МКНФ, но и в базисах Пирса и Шеффера.
В начале рассмотрим получение МДНФ.
Минимизация булевых функций методом подбора
кратчайших претендентов.
При использовании метода булева функция представляется матрицей наборов аргументов, на которых функция равна единице (матрица единиц) и матрицей наборов, на которых функция равна нулю (матрица нулей). Под претендентом будем понимать в зависимости от требуемой формы представления функции произведение, сумму, функцию Шеффера, либо функцию Пирса над аргументами, взятые с отрицанием, либо без него. При получении МДНФ претендент – произведение аргументов. При получении МКНФ претендент – сумма аргументов, при минимизации в базисах Шеффера и Пирса – претендент операция И-НЕ и ИЛИ-НЕ над аргументами.
Число аргументов претендента будем называть длиной претендента.
Рассмотрим метод получения МДНФ методом подбора кратчайших произведений.
Пример. Задана не полностью определенная булева функция
, 
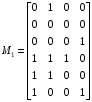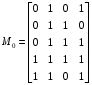
Берем первый набор матрицы единиц 0100. Произведения, покрывающие этот набор, рассматриваются как претенденты на вхождение в минимальную форму:
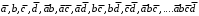
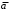- не подходит, поскольку оно равно 1 не только на 0100 матрицы единиц, но и на наборах 0101, 0110, 0111 матрицы нулей; - не подходит, поскольку равно 1 на всех наборах матрицы нулей;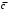
-не подходит, т.к. равно 1 на наборах 0101, 1101 матрицы нулей;
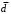- не подходит, т.к. равно 1 на наборе 0110;
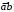-не подходит, т.к. равно 1 на наборе 0101, 0110, 0111;
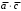- не подходит, т.к. равно 1 на наборе 0101;
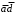- не подходит, т.к. равно 1 на наборе 0110;
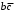- не подходит, т.к. равно 1 на наборах 0101 и 1101;
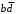- не подходит, т.к. равно 1 на наборе 0110;
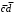-подходит, поскольку не равно 1 ни на одном наборе матрицы нулей и покрывает наборы 0100, 0000 матрицы единиц.Вписываем
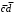в МДНФ и удаляем наборы 0100 и 0000 из матрицы единиц: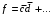 
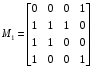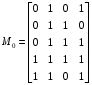
, Выписываем набор 0001 матрицы единиц и аналогично ищем кратчайшее произведение равное единице на этом наборе:
- не подходит, поскольку дает значение 1 наборам 0101, 0110, 0111 матрицы нулей;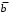
-подходит, поскольку не равно 1 ни на одном наборе матрицы нулей и покрывает наборы 0001, 1001 матрицы единиц. Вписываем 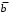в МДНФ и удаляем наборы 0001 и 1001 в матрице единиц: 
, 
, 
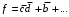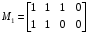.Выписываем набор 1110 и, поочередно рассматривая претенденты
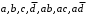, находим кратчайшее произведение 
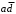равное 1 на наборах 1110 и 1100 и равное нулю на всех наборах матрицы нулей. Вычеркиваем наборы 1110 и 1100 из матрицы единиц. Поскольку матрица единиц пуста – минимизация закончена. МДНФ имеет вид: 
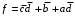.Замечание: если искать покрытие матрицы единиц функцией Шеффера с минимальным числом аргументов, то получим минимальную форму в базисе Шеффера. Естественно, что следует учитывать особенности этой функции:
- если претендент, покрывающий набор матрицы единиц и равный нулю на всех наборах матрицы нулей состоит из одного аргумента, он должен записываться в минимальную форму с дополнительным отрицанием;
- если претендент покрывает все наборы матрицы единиц и равен нулю на всех наборах матрицы нулей, то он записывается с общим отрицанием. Для рассмотренного примера претенденты, которые входят в минимальную форму:
,
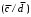