ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 89
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Свойства функций Шеффера, Пирса, суммы по модулю 2.
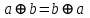 ,
, 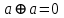 ,
, 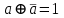 ,
,
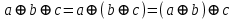 ,
, 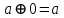 ,
, 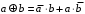 .
.
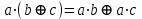 ,
, 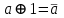 .
.
Для функций Шеффера и Пирса имеет место переместительный закон:
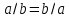 ,
, 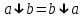 ,
,
Но сочетательный закон для них НЕ справедлив!
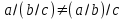 ,
, 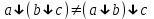 ,
,
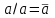 ,
, 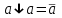 ,
,
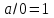 ,
, 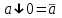 ,
,
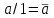 ,
, 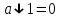 ,
,
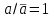 ,
, 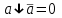 .
.
Существуют тождества похожие на правила де Моргана:
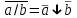 ,
, 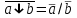 .
.
На практике часто возникает необходимость преобразовать функцию, аргументы которой связаны операцией Шеффера или Пирса к выражению, содержащему только операции конъюнкции, дизъюнкции и отрицания. Если символы отрицания расположены над одиночными символами переменных, то такая булева функция называется нормальной. Именно такие представления функций наиболее просто воспринимаются человеком. Для подобного преобразования в литературе обычно используют правила де Моргана, однако существует очень простой прием, позволяющий сразу записать искомый результат:
1) заменить в выражении операции Пирса и Шеффера на операции И-НЕ и ИЛИ-НЕ соответственно;
2) подсчитать число инверсий над каждой буквой, если оно четно, то в преобразуемое выражение эта буква будет входить без отрицания, если нечетно – с отрицанием;
3) подсчитать число инверсий над каждой логической операцией, если число инверсий четно, то операция не меняется, если нечетно, то логическая операция заменяется дуальной логической операцией.
Пример:
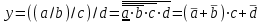
Для функций Шеффера и Пирса можно вывести тождества, похожие на правила склеивания:
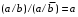 ,
, 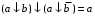
действительно,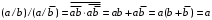 ,
,
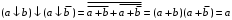 ,
,
Аналитическая запись булевых функций в булевом базисе.
Определение: конституентой единицы булевой функции называют произведение всех ее аргументов, записанных с отрицанием или без него.
Пример: если рассмотреть функцию трех аргументов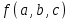 , то
, то
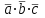 ,
, 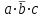 ,
,  -конституенты единицы. Напишем несколько выражений не являющихся конституентами единицы:
-конституенты единицы. Напишем несколько выражений не являющихся конституентами единицы:  (не все аргументы),
(не все аргументы), 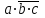 - используя правило де Моргана, получим:
- используя правило де Моргана, получим: 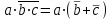 , а это противоречит определению конституенты единицы.
, а это противоречит определению конституенты единицы.
Следствие: любая конституента единицы равна единице только на одном наборе аргументов, на остальных наборах эта конституента равна нулю.
Для того чтобы определить набор на котором конституента единицы равна 1 следует найти такие значения аргументов, которые дают значение 1 каждому члену произведения. Пример: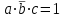 , если
, если 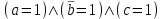 , а это возможно только на наборе 101.
, а это возможно только на наборе 101.
Теорема: Любая булева функция может быть записана в виде дизъюнкции конституент единицы, соответствующих тем наборам на которых функция равна 1.
Доказательство. Выберем в таблице истинности произвольный набор. При этом возможны два случая:
Если на данном наборе функция равна 1, то из множества конституент выберем конституенту равную 1 на этом наборе (на остальных наборах она будет равна нулю) и записываем ее в формулу. Учитывая свойство дизъюнкции 1+…=1, мы обеспечиваем единичное значение функции на этом наборе.
Если на этом наборе функция равна нулю, то конституента равная 1 на этом наборе в формулу не вписывается, а значит на этом наборе функция будет равна 0.
После рассмотрения всех наборов мы получим аналитическую запись булевой функции в
дизъюнктивной совершенной нормальной форме (ДСНФ).
Алгоритм перехода к ДСНФ:
- Выбрать в таблице истинности все наборы на которых функция равна единице.
- Записать конституенты 1 равные единице на этих наборах. При этом, если аргумент в наборе равен 1, то в конституенту единицы этого набора он записывается без отрицания. Если же аргумент в наборе равен нулю, то он записывается с отрицанием.
- Полученные конституенты соединить операцией дизъюнкции.

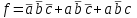
Пример:
Определение: конституентой нуля называют дизъюнкцию всех переменных, записанных с отрицанием или без него.
Любая конституента нуля равна нулю только на одном наборе, на остальных наборах она равна 1.
Теорема. Любая булева функция может быть записана как конъюнкция конституент нуля, записанных для наборов, где функция равна нулю.
Доказательство. Выбираем в таблице истинности произвольный набор. Если на этом наборе функция равна нулю, то записываем конституенту нуля равную нулю на этом наборе. Поскольку свойство конъюнкции
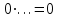 , то на данном наборе функция будет равна нулю. Если же функция равна на наборе 1, то конституенту нуля равную нулю на этом наборе не выписываем, а т.к. остальные конституенты на этом наборе равны 1, то и их произведение будет равно 1. Такая запись булевой функции называется конъюнктивной совершенной нормальной формой (КСНФ).
, то на данном наборе функция будет равна нулю. Если же функция равна на наборе 1, то конституенту нуля равную нулю на этом наборе не выписываем, а т.к. остальные конституенты на этом наборе равны 1, то и их произведение будет равно 1. Такая запись булевой функции называется конъюнктивной совершенной нормальной формой (КСНФ).
Алгоритм перехода к КСНФ:
-Выбрать в таблице истинности наборы на которых функция равна нулю.
-Записать конституенты нуля равные нулю на этих наборах. Для этого, если аргумент набора равен нулю, то он входит в конституенту без отрицания, если же аргумент входит в набор как 1, то в соответствующую конституенту нуля вписывается его отрицание.
-Все записанные конституенты нуля соединяем знаком конъюнкции.
Запишем КСНФ для функции из предыдущего примера:
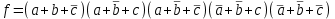 .
.
Дешифраторы.
При работе с дискретными устройствами приходится решать задачи анализа схем и задачи синтеза схем. При решении задачи синтеза после получения технического задания на проектирование устройства составляется математическая модель устройства, а затем разрабатывается схема устройства. Задача анализа обратная задаче синтеза. Решим задачу анализа, рассматривая схему простейшего дешифратора с прямыми выходами.
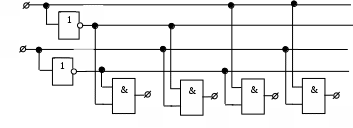
В схеме два входа ,
,  и четыре выхода, которые описываются булевыми уравнениями:
и четыре выхода, которые описываются булевыми уравнениями: 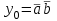 ,
, 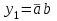 ,
, 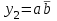 ,
, 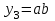 . Построим таблицы истинности для этих уравнений:
. Построим таблицы истинности для этих уравнений:
Свойства функций Шеффера, Пирса, суммы по модулю 2.
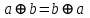 ,
, 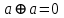 ,
, 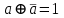 ,
,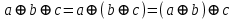 ,
, 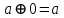 ,
, 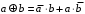 .
.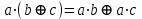 ,
, 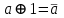 .
.Для функций Шеффера и Пирса имеет место переместительный закон:
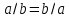 ,
, 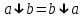 ,
,Но сочетательный закон для них НЕ справедлив!
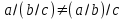 ,
, 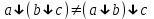 ,
,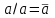 ,
, 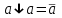 ,
,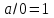 ,
, 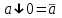 ,
,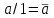 ,
, 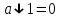 ,
,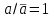 ,
, 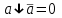 .
.Существуют тождества похожие на правила де Моргана:
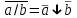 ,
, 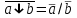 .
.На практике часто возникает необходимость преобразовать функцию, аргументы которой связаны операцией Шеффера или Пирса к выражению, содержащему только операции конъюнкции, дизъюнкции и отрицания. Если символы отрицания расположены над одиночными символами переменных, то такая булева функция называется нормальной. Именно такие представления функций наиболее просто воспринимаются человеком. Для подобного преобразования в литературе обычно используют правила де Моргана, однако существует очень простой прием, позволяющий сразу записать искомый результат:
1) заменить в выражении операции Пирса и Шеффера на операции И-НЕ и ИЛИ-НЕ соответственно;
2) подсчитать число инверсий над каждой буквой, если оно четно, то в преобразуемое выражение эта буква будет входить без отрицания, если нечетно – с отрицанием;
3) подсчитать число инверсий над каждой логической операцией, если число инверсий четно, то операция не меняется, если нечетно, то логическая операция заменяется дуальной логической операцией.
Пример:
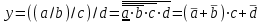
Для функций Шеффера и Пирса можно вывести тождества, похожие на правила склеивания:
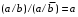 ,
, 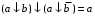
действительно,
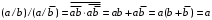 ,
,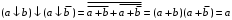 ,
,Аналитическая запись булевых функций в булевом базисе.
Определение: конституентой единицы булевой функции называют произведение всех ее аргументов, записанных с отрицанием или без него.
Пример: если рассмотреть функцию трех аргументов
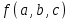 , то
, то 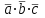 ,
, 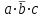 ,
,  -конституенты единицы. Напишем несколько выражений не являющихся конституентами единицы:
-конституенты единицы. Напишем несколько выражений не являющихся конституентами единицы:  (не все аргументы),
(не все аргументы), 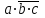 - используя правило де Моргана, получим:
- используя правило де Моргана, получим: 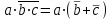 , а это противоречит определению конституенты единицы.
, а это противоречит определению конституенты единицы.Следствие: любая конституента единицы равна единице только на одном наборе аргументов, на остальных наборах эта конституента равна нулю.
Для того чтобы определить набор на котором конституента единицы равна 1 следует найти такие значения аргументов, которые дают значение 1 каждому члену произведения. Пример:
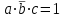 , если
, если 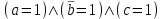 , а это возможно только на наборе 101.
, а это возможно только на наборе 101.Теорема: Любая булева функция может быть записана в виде дизъюнкции конституент единицы, соответствующих тем наборам на которых функция равна 1.
Доказательство. Выберем в таблице истинности произвольный набор. При этом возможны два случая:
Если на данном наборе функция равна 1, то из множества конституент выберем конституенту равную 1 на этом наборе (на остальных наборах она будет равна нулю) и записываем ее в формулу. Учитывая свойство дизъюнкции 1+…=1, мы обеспечиваем единичное значение функции на этом наборе.
Если на этом наборе функция равна нулю, то конституента равная 1 на этом наборе в формулу не вписывается, а значит на этом наборе функция будет равна 0.
После рассмотрения всех наборов мы получим аналитическую запись булевой функции в
дизъюнктивной совершенной нормальной форме (ДСНФ).
Алгоритм перехода к ДСНФ:
- Выбрать в таблице истинности все наборы на которых функция равна единице.
- Записать конституенты 1 равные единице на этих наборах. При этом, если аргумент в наборе равен 1, то в конституенту единицы этого набора он записывается без отрицания. Если же аргумент в наборе равен нулю, то он записывается с отрицанием.
- Полученные конституенты соединить операцией дизъюнкции.

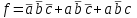
Пример:
 |  | с |  |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Определение: конституентой нуля называют дизъюнкцию всех переменных, записанных с отрицанием или без него.
Любая конституента нуля равна нулю только на одном наборе, на остальных наборах она равна 1.
Теорема. Любая булева функция может быть записана как конъюнкция конституент нуля, записанных для наборов, где функция равна нулю.
Доказательство. Выбираем в таблице истинности произвольный набор. Если на этом наборе функция равна нулю, то записываем конституенту нуля равную нулю на этом наборе. Поскольку свойство конъюнкции
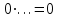 , то на данном наборе функция будет равна нулю. Если же функция равна на наборе 1, то конституенту нуля равную нулю на этом наборе не выписываем, а т.к. остальные конституенты на этом наборе равны 1, то и их произведение будет равно 1. Такая запись булевой функции называется конъюнктивной совершенной нормальной формой (КСНФ).
, то на данном наборе функция будет равна нулю. Если же функция равна на наборе 1, то конституенту нуля равную нулю на этом наборе не выписываем, а т.к. остальные конституенты на этом наборе равны 1, то и их произведение будет равно 1. Такая запись булевой функции называется конъюнктивной совершенной нормальной формой (КСНФ). Алгоритм перехода к КСНФ:
-Выбрать в таблице истинности наборы на которых функция равна нулю.
-Записать конституенты нуля равные нулю на этих наборах. Для этого, если аргумент набора равен нулю, то он входит в конституенту без отрицания, если же аргумент входит в набор как 1, то в соответствующую конституенту нуля вписывается его отрицание.
-Все записанные конституенты нуля соединяем знаком конъюнкции.
Запишем КСНФ для функции из предыдущего примера:
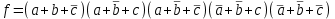 .
.Дешифраторы.
При работе с дискретными устройствами приходится решать задачи анализа схем и задачи синтеза схем. При решении задачи синтеза после получения технического задания на проектирование устройства составляется математическая модель устройства, а затем разрабатывается схема устройства. Задача анализа обратная задаче синтеза. Решим задачу анализа, рассматривая схему простейшего дешифратора с прямыми выходами.

В схеме два входа
 ,
,  и четыре выхода, которые описываются булевыми уравнениями:
и четыре выхода, которые описываются булевыми уравнениями: 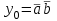 ,
, 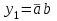 ,
, 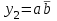 ,
, 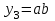 . Построим таблицы истинности для этих уравнений:
. Построим таблицы истинности для этих уравнений:  |  |  |  |  |  Видно, что такой дешифратор формирует на своих выходах все конституенты единицы булевых функций двух аргументов: 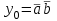 , ,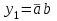 , , 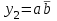 , , 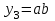 . . |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |