ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 95
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
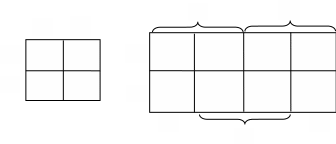
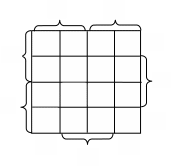
Диаграммы Вейча для функции 2 и 3 аргументов соответственно.
Для правильной разметки достаточно отводить половину таблицы под аргумент, а другую половину таблицы – под инверсию аргумента, при этом скобки на противоположных сторонах таблицы не должны совпадать! Естественно, что возможно несколько вариантов разметки одной и той же таблицы.
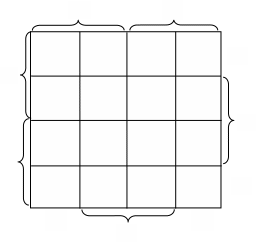
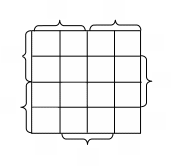
Диаграмма Вейча для функции четырех аргументов.
Все клетки, которые отличаются значением только одной переменной, являются соседними. Для функции пяти и более переменных эти клетки могут быть расположены не рядом. Пример: клетке 3 соответствует конституента единицы
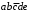. Клеткам 2, 4, 6, 27 – конституенты единицы 
, 
, 
, 
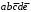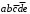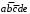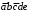. Все эти клетки соседние для клетки 3.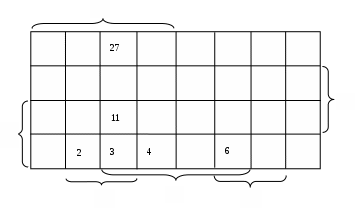
При минимизации следует руководствоваться следующими правилами:
1) Строится и размечается прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов.
2) В клетки таблицы заносятся значения булевой функции. При поиске клеточки таблицы аргумент набора равный 1 берется без отрицания, а равный нулю – с отрицанием. В найденную клетку записывают значение функции.
3) Обводят контурами все 1 с соблюдением следующих правил:
- контур должен быть прямоугольным;
- внутри контура не должно быть нулей;
- при обводке следует получить минимальное число контуров максимальной площади;
- число единиц в контуре должно быть равно степени числа 2 (1, 2, 4, 8, 16,…);
- одна и та же клетка, заполненная единицей может входить в несколько контуров;
- при обводке следует учитывать, что самая верхняя и самая нижняя строки таблицы являются соседними. Соседними являются также крайний левый и крайний правый столбцы.
- количество контуров должно быть как можно меньше, а площадь контуров – как можно больше.
4) Записывают минимальное выражение как дизъюнкцию логических произведений, которые описывают контура таблицы. Для поиска логического выражения для контура выясняют от каких аргументов он зависит. Если все 1 контура приписаны к аргументу
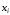, то в логическое произведение этот аргумент входит. Если все единицы контура помечены инверсией аргумента, то в произведение вписывается 
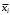. Если в контуре есть 1, помеченные 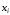и 1, помеченные 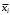, то в описание контура этот аргумент не входит.Минимизируемая функция должна быть задана таблицей, либо дизъюнктивной нормальной формой.
Пример: Найти МДНФ функции
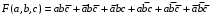
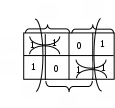
В этом таблице три контура. Один из них «разрезан» при развертке тора. Минимальное выражение:
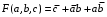
Пример: минимизировать не полностью определенную булеву функцию, заданную таблицей.
 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
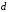 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
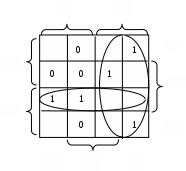
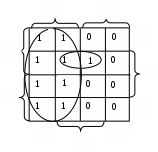
В данном примере не полностью определенная функция была доопределена таким образом, чтобы получить минимальное число контуров максимальной площади, что обеспечивает наиболее простое логическое выражение функции. Естественно, что обведенные пустые клетки доопределены единицами, а не обведенные – нулями. Результат:
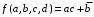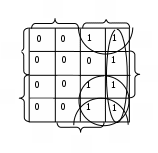
.В некоторых случаях МДНФ инверсной функции проще, чем МДНФ исходной функции. Пример:
| | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
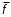 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
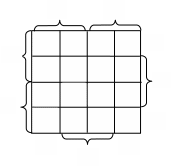
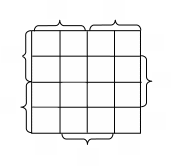
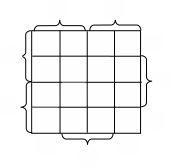
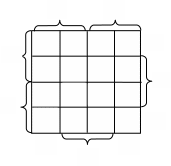
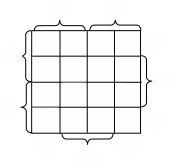
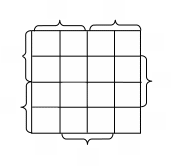
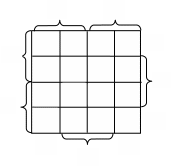
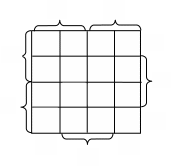
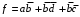
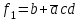
Минимизация булевых функции в базисе Шеффера.
Обычно, при необходимости получения минимального выражения в базисе Пирса или Шеффера функцию минимизируют в булевом базисе, а затем, используя правила де Моргана, преобразуют функцию.
Пример: запишем функции
и 
в базисе Шеффера: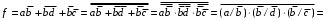 
;
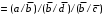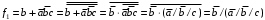.Однако, ранее рассмотренные свойства операций Шеффера и Пирса позволяют записывать минимальные формы функций в базисах Шеффера и Пирса используя диаграммы Вейча.
Минимизация булевых функции в базисе Шеффера
с помощью диаграмм Вейча.
При использовании диаграмм Вейча строится прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов. Каждой клетке этой таблицы соответствует набор аргументов и
- местная функция Шеффера, где - число аргументов функции, равная единице на этом наборе. Требуется, чтобы в соседних клетках эти функции отличались только одним аргументом.При минимизации следует руководствоваться следующими правилами:
1) Строится и размечается прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов.
2) В клетки таблицы заносятся значения булевой функции. При поиске клеточки таблицы аргумент набора равный 1 берется без отрицания, а равный нулю – с отрицанием. В найденную клетку записывают значение функции.
3) Обводят контурами все 1 с соблюдением следующих правил:
- контур должен быть прямоугольным;
- внутри контура не должно быть нулей;
- при обводке следует получить минимальное число контуров максимальной площади;
- число единиц в контуре должно быть равно степени числа 2 (1, 2, 4, 8, 16,…);
- одна и та же клетка, заполненная единицей может входить в несколько контуров;
- при обводке следует учитывать, что самая верхняя и самая нижняя строки таблицы являются соседними. Соседними являются также крайний левый и крайний правый столбцы.
- количество контуров должно быть как можно меньше, а площадь контуров – как можно больше.
4) Записывают минимальное выражение как функцию Шеффера над логическими выражениями, которые описывают контура таблицы. Логическое выражение для контура представляет собой операцию Шеффера от аргументов. Для поиска логического выражения для контура выясняют, от каких аргументов он зависит. Если все 1 контура приписаны к аргументу
, то в логическое выражение этот аргумент входит. Если все единицы контура помечены инверсией аргумента, то в выражение вписывается 
. Если в контуре есть 1, помеченные и 1, помеченные , то в описание контура этот аргумент не входит.ВАЖНО! При минимизации в базисах Шеффера и Пирса действуют два дополнительных правила:
1) Если контур занимает половину таблицы, то над аналитическим описанием этого контура ставится дополнительное отрицание;
2) Если в таблице только один контур, то над ним также следует поставить дополнительное отрицание.
Естественно, если в таблице только один контур, и он занимает половину таблицы, то над ним ставятся два дополнительных отрицания.
Эти особенности обусловлены тем, что базисы Шеффера (И-НЕ) и Пирса (ИЛИ-НЕ) связаны с инвертированием операции И или операции ИЛИ над аргументами. Минимальное выражение – это функция Шеффера (Пирса) над логическими описаниями контуров. Если в таблице один контур, то при выполнении функции Шеффера получим:
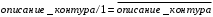, т.е нужно дополнительное отрицание. Описание контура – это функция Шеффера (Пирса) над аргументами, от которых этот контур зависит. Если он занимает половину таблицы, то он зависит от одного аргумента и поэтому над ним следует поставить дополнительное отрицание.
Пример: минимизировать в базисе Шеффера функции:
| | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
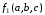 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
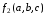 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
, 
, 
, 
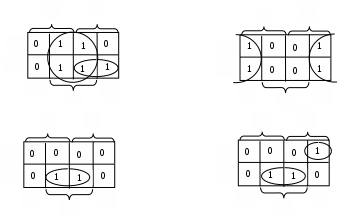
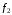
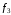
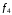
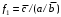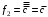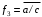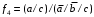.Очевидно Вы заметили, что правила заполнения и обводки одинаковы при минимизации в базисе Шеффера и при получении минимальных дизъюнктивных нормальных форм. Следовательно, МДНФ можно получить из этих же таблиц:
, 
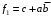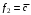
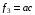
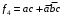.Получение минимальных конъюнктивных нормальных
форм с помощью диаграмм Вейча.
При использовании диаграмм Вейча строится прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов. Каждой клетке этой таблицы соответствует набор аргументов и конституента нуля, равная нулю на этом наборе. Требуется, чтобы в соседних клетках эти конституенты отличались только одним сомножителем.
При минимизации следует руководствоваться следующими правилами:
1) Строится и размечается прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов.
2) В клетки таблицы заносятся значения булевой функции. При поиске клеточки таблицы аргумент набора равный 0 берется без отрицания, а равный 1 – с отрицанием. В найденную клетку записывают значение функции.
3) Обводят контурами все нули с соблюдением следующих правил:
- контур должен быть прямоугольным;
- внутри контура не должно быть единиц;
- при обводке следует получить минимальное число контуров максимальной площади;
- число нулей в контуре должно быть равно степени числа 2 (1, 2, 4, 8, 16,…);
- одна и та же клетка, заполненная нулем может входить в несколько контуров;
- при обводке следует учитывать, что самая верхняя и самая нижняя строки таблицы являются соседними. Соседними являются также крайний левый и крайний правый столбцы.
- количество контуров должно быть как можно меньше, а площадь контуров – как можно больше.
4) Записывают минимальное выражение как конъюнкцию логических сумм, которые описывают контура таблицы. Для поиска логического выражения для контура выясняют от каких аргументов он зависит. Если все нули контура приписаны к аргументу
, то в логическое произведение этот аргумент входит. Если все нули контура помечены инверсией аргумента, то в произведение вписывается . Если в контуре есть 0, помеченные и 0, помеченные , то в описание контура этот аргумент не входит.Пример: минимизировать не полностью определенную булеву функцию, заданную таблицей.
| | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
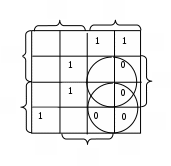
В данном примере не полностью определенная функция была доопределена таким образом, чтобы получить минимальное число контуров максимальной площади, что обеспечивает наиболее простое логическое выражение функции. Естественно, что обведенные пустые клетки доопределены нулями, а не обведенные – единицами. Результат:
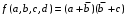.Минимизация булевых функции в базисе Пирса
с помощью диаграмм Вейча.
При использовании диаграмм Вейча строится прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов. Каждой клетке этой таблицы соответствует набор аргументов и
- местная функция Пирса, где - число аргументов функции, равная нулю на этом наборе. Требуется, чтобы в соседних клетках эти функции отличались только одним аргументом.