ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 91
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 
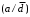, а минимальное выражение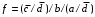 
Видно, что при работе алгоритма многократно проверяются уже отвергнутые претенденты, что сильно увеличивает время, затрачиваемое на минимизацию. Рассмотрим модификацию алгоритма свободного от этого недостатка на примере получения МДНФ.
Рассматривается матрица нулей и формируется очередь допустимых претендентов, описываемых одним аргументом. Допустимым будет претендент, который равен нулю на всех наборах матрицы нулей. Если допустимый претендент покрывает хотя бы один набор матрицы единиц, он вписывается в формулу, а покрываемые наборы исключаются из матрицы единиц. Если – нет, то претендент в формулу не входит и рассматривается следующий допустимый претендент из очереди. Если все наборы матрицы единиц удалены, работа алгоритма закончена, если же нет, рассматривается следующий допустимый претендент из очереди, а если очередь пуста, то формируется новая очередь допустимых претендентов, зависящих уже от двух аргументов и т.д.
Алгоритм получения МДНФ:
1) Задать длину претендента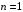
;
2) Рассматривая матрицу нулей сформировать очередь всех допустимых претендентов длины
;
3) Если очередь пуста, принять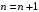
и перейти к пункту 2, иначе – к пункту 4;
4) Взять первого допустимого претендента из очереди и проверить покрывает ли он хотя бы один набор в матрице единиц. Если – нет, то допустимый претендент удалить из очереди и перейти к пункту 3, если – да, то перейти к пункту 5.
5) Включить допустимый претендент в формулу, представляющую собой сумму претендентов;
6) Исключить наборы, покрываемые претендентом из матрицы единиц;
7) Исключить претендент из очереди;
8) Если матрица единиц не пуста, то перейти к пункту 3, иначе – конец.
В рассматриваемом примере претенденты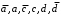
недопустимы, поскольку обращают в единицу один или несколько наборов матрицы нулей.
Очередь состоит только из одного допустимого претендента
, который равен нулю на всех наборах матрицы нулей. Этот претендент покрывает
наборы 0000, 0001,1001 матрицы единиц, поэтому он входит в формулу
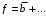. Матрица единиц после удаления этих наборов примет вид:
, 
.
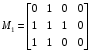Поскольку после удаления очередь пуста, формируем очередь допустимых претендентов, зависящих от двух аргументов: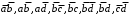 
.
Допустимые претенденты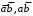
не покрывают ни одного набора матрицы единиц и удаляются. Допустимый претендент 
покрывает наборы 1110 и 1100 матрицы единиц, поэтому он вписывается в формулу, а наборы 1110 и 1100 исключаются из матрицы единиц: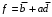 
,
, .
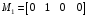Допустимые претенденты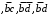
не покрывают набора 0101 и исключаются. Допустимый претендент 
покрывает набор 0101, следовательно, он входит в формулу: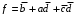 
. Поскольку матрица единиц после удаления набора 0100 пуста – минимизация закончена.
Получение МКНФ и минимальных форм в базисе Пирса.
В этих базисах допустимые претенденты ищут, рассматривая матрицу единиц. Рассмотрим алгоритм получения МКНФ. Претендентом служит сумма аргументов взятых с отрицанием или без него.
1) Задать длину претендента
;
2) Рассматривая матрицу единиц сформировать очередь всех допустимых претендентов длины ;
3) Если очередь пуста, принять
и перейти к пункту 2, иначе – к пункту 4;
4) Взять первого допустимого претендента из очереди и проверить обнуляет ли он хотя бы один набор в матрице нулей. Если – нет, то допустимый претендент удалить из очереди и перейти к пункту 3, если – да, то перейти к пункту 5.
5) Включить допустимый претендент в формулу, представляющую собой произведение претендентов;
6) Исключить наборы матрицы нулей, на которых допустимый претендент равен нулю;
7) Исключить претендент из очереди;
8) Если матрица нулей не пуста, то перейти к пункту 3, иначе – конец.
Рассмотрим получение МДНФ той же функции:
,
Претенденты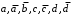
недопустимы, потому что обращают в нуль хотя бы один набор матрицы единиц.
Из претендентов длины 2 в очередь допустимых претендентов входят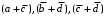
. Допустимый претендент 
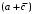равен нулю на наборах 0101 и 0110 матрицы нулей, поэтому он входит в МКНФ:
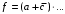. После исключения наборов 0101, 0110, 0111 получим:
, 
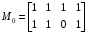. Следующий допустимый претендент из очереди 
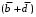равен нулю на наборах 1111 и 1101 матрицы нулей, т.е. входит в МКНФ: 
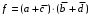. Т.к. после удаления наборов матрица нулей пуста – минимизация закончена.
Замечание: если искать допустимые претенденты в виде функции Пирса с минимальным числом аргументов, которые равны нулю хотя бы на одном наборе матрицы нулей и равны единице на всех наборах матрицы единиц, то получим минимальную форму в базисе Пирса. Естественно, что следует учитывать особенности этой функции:
- если претендент, равный нулю на наборе матрицы нулей и равный единице на всех наборах матрицы единиц состоит из одного аргумента, он должен записываться в минимальную форму с дополнительным отрицанием;
- если претендент равен нулю на всех наборах матрицы нулей и равен единице на всех наборах матрицы единиц, то он записывается с общим отрицанием. Для рассмотренного примера допустимые претенденты, которые входят в минимальную форму:
, 
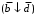, а минимальное выражение 
.
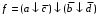Замечание. При минимизации функций большого числа аргументов, матрицы единиц и нулей занимают значительный объем памяти ЭВМ. При большом числе аргументов его можно уменьшить более чем на порядок, если применить следующий прием: для минимизируемой функции выделяются две матрицы размером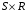
,
где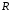
- число разрядов в машинном слове;
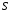- выделенное число слов.
Число слов матрицы при минимизации функции аргументов определяется по формул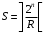е:
, где 
-символ округления результата к большему целому. Номер набора в матрице определяется его положением:
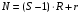, где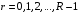 
- номер разряда в слове.
Пример: в гипотетической четырехразрядной машине задана матрица
Разряд 3 2 1 0
Слово 0 0 0 0 1
Слово 1 0 1 1 0
Слово 2 1 0 0 0
Слово 3 1 0 0 1
Единицы этой матрицы соответствуют наборам 0,5,6,10,11,12,15.
Минимизируемую функцию задают двумя подобными матрицами.
Исходно эти матрицы заполняются нулями. Затем в матрицу единиц вписывают единицы в позиции, которые соответствуют наборам на которых функция равна единице, а в матрицу нулей вписывают единицы в позиции, которые соответствуют наборам на которых функция равна нулю.
Пример:
, 
.
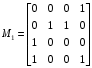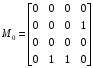Эти матрицы задают не полностью определенную функцию равную единице на наборах 0,5,6,11,12,15 и нулю на наборах 4,13,14.
Нетрудно подсчитать, что число слов в каждой из матриц при минимизации функций 32 аргументов на 32-разрядных машинах составит 134217728. Такой объем оперативной памяти доступен для современных ЭВМ. Главными ограничениями метода являются приемлемое время ввода значений функции и время собственно минимизации функции. Однако не следует смотреть на проблему минимизации слишком пессимистично, т.к. известно, что реальные булевы функции большого числа аргументов в подавляющем большинстве случаев не определены, причем число неопределенных наборов возрастает с ростом числа аргументов булевой функции.
Синтез комбинационных схем.
Существует класс логических устройств, у которых выходные сигналы схемы в данный момент времени зависят только от комбинации входных сигналов поступивших на схему в данный момент времени:
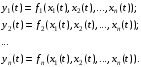
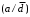, а минимальное выражение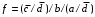 Видно, что при работе алгоритма многократно проверяются уже отвергнутые претенденты, что сильно увеличивает время, затрачиваемое на минимизацию. Рассмотрим модификацию алгоритма свободного от этого недостатка на примере получения МДНФ.
Рассматривается матрица нулей и формируется очередь допустимых претендентов, описываемых одним аргументом. Допустимым будет претендент, который равен нулю на всех наборах матрицы нулей. Если допустимый претендент покрывает хотя бы один набор матрицы единиц, он вписывается в формулу, а покрываемые наборы исключаются из матрицы единиц. Если – нет, то претендент в формулу не входит и рассматривается следующий допустимый претендент из очереди. Если все наборы матрицы единиц удалены, работа алгоритма закончена, если же нет, рассматривается следующий допустимый претендент из очереди, а если очередь пуста, то формируется новая очередь допустимых претендентов, зависящих уже от двух аргументов и т.д.
Алгоритм получения МДНФ:
1) Задать длину претендента
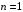;2) Рассматривая матрицу нулей сформировать очередь всех допустимых претендентов длины
;3) Если очередь пуста, принять
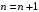и перейти к пункту 2, иначе – к пункту 4;4) Взять первого допустимого претендента из очереди и проверить покрывает ли он хотя бы один набор в матрице единиц. Если – нет, то допустимый претендент удалить из очереди и перейти к пункту 3, если – да, то перейти к пункту 5.
5) Включить допустимый претендент в формулу, представляющую собой сумму претендентов;
6) Исключить наборы, покрываемые претендентом из матрицы единиц;
7) Исключить претендент из очереди;
8) Если матрица единиц не пуста, то перейти к пункту 3, иначе – конец.
В рассматриваемом примере претенденты
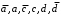недопустимы, поскольку обращают в единицу один или несколько наборов матрицы нулей.Очередь состоит только из одного допустимого претендента
, который равен нулю на всех наборах матрицы нулей. Этот претендент покрывает наборы 0000, 0001,1001 матрицы единиц, поэтому он входит в формулу
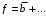. Матрица единиц после удаления этих наборов примет вид: 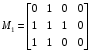, .Поскольку после удаления
очередь пуста, формируем очередь допустимых претендентов, зависящих от двух аргументов: 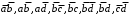. Допустимые претенденты
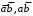не покрывают ни одного набора матрицы единиц и удаляются. Допустимый претендент покрывает наборы 1110 и 1100 матрицы единиц, поэтому он вписывается в формулу, а наборы 1110 и 1100 исключаются из матрицы единиц: 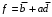, , 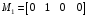.Допустимые претенденты
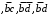не покрывают набора 0101 и исключаются. Допустимый претендент покрывает набор 0101, следовательно, он входит в формулу: 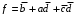. Поскольку матрица единиц после удаления набора 0100 пуста – минимизация закончена.
Получение МКНФ и минимальных форм в базисе Пирса.
В этих базисах допустимые претенденты ищут, рассматривая матрицу единиц. Рассмотрим алгоритм получения МКНФ. Претендентом служит сумма аргументов взятых с отрицанием или без него.
1) Задать длину претендента
;2) Рассматривая матрицу единиц сформировать очередь всех допустимых претендентов длины
;3) Если очередь пуста, принять
и перейти к пункту 2, иначе – к пункту 4;4) Взять первого допустимого претендента из очереди и проверить обнуляет ли он хотя бы один набор в матрице нулей. Если – нет, то допустимый претендент удалить из очереди и перейти к пункту 3, если – да, то перейти к пункту 5.
5) Включить допустимый претендент в формулу, представляющую собой произведение претендентов;
6) Исключить наборы матрицы нулей, на которых допустимый претендент равен нулю;
7) Исключить претендент из очереди;
8) Если матрица нулей не пуста, то перейти к пункту 3, иначе – конец.
Рассмотрим получение МДНФ той же функции:
, Претенденты
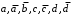недопустимы, потому что обращают в нуль хотя бы один набор матрицы единиц.Из претендентов длины 2 в очередь допустимых претендентов входят
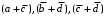. Допустимый претендент 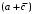равен нулю на наборах 0101 и 0110 матрицы нулей, поэтому он входит в МКНФ:
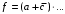. После исключения наборов 0101, 0110, 0111 получим: , 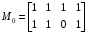. Следующий допустимый претендент из очереди 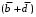равен нулю на наборах 1111 и 1101 матрицы нулей, т.е. входит в МКНФ: 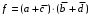. Т.к. после удаления наборов матрица нулей пуста – минимизация закончена.Замечание: если искать допустимые претенденты в виде функции Пирса с минимальным числом аргументов, которые равны нулю хотя бы на одном наборе матрицы нулей и равны единице на всех наборах матрицы единиц, то получим минимальную форму в базисе Пирса. Естественно, что следует учитывать особенности этой функции:
- если претендент, равный нулю на наборе матрицы нулей и равный единице на всех наборах матрицы единиц состоит из одного аргумента, он должен записываться в минимальную форму с дополнительным отрицанием;
- если претендент равен нулю на всех наборах матрицы нулей и равен единице на всех наборах матрицы единиц, то он записывается с общим отрицанием. Для рассмотренного примера допустимые претенденты, которые входят в минимальную форму:
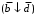, , а минимальное выражение 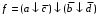.Замечание. При минимизации функций большого числа аргументов, матрицы единиц и нулей занимают значительный объем памяти ЭВМ. При большом числе аргументов его можно уменьшить более чем на порядок, если применить следующий прием: для минимизируемой функции выделяются две матрицы размером
,
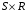
где
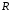- число разрядов в машинном слове; 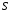- выделенное число слов.Число слов матрицы при минимизации функции
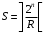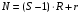аргументов определяется по формуле: , где -символ округления результата к большему целому. Номер набора в матрице определяется его положением: , где 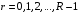- номер разряда в слове.Пример: в гипотетической четырехразрядной машине задана матрица
Разряд 3 2 1 0
Слово 0 0 0 0 1
Слово 1 0 1 1 0
Слово 2 1 0 0 0
Слово 3 1 0 0 1
Единицы этой матрицы соответствуют наборам 0,5,6,10,11,12,15.
Минимизируемую функцию задают двумя подобными матрицами.
Исходно эти матрицы заполняются нулями. Затем в матрицу единиц вписывают единицы в позиции, которые соответствуют наборам на которых функция равна единице, а в матрицу нулей вписывают единицы в позиции, которые соответствуют наборам на которых функция равна нулю.
Пример:
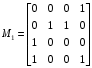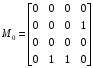, .Эти матрицы задают не полностью определенную функцию равную единице на наборах 0,5,6,11,12,15 и нулю на наборах 4,13,14.
Нетрудно подсчитать, что число слов в каждой из матриц при минимизации функций 32 аргументов на 32-разрядных машинах составит 134217728. Такой объем оперативной памяти доступен для современных ЭВМ. Главными ограничениями метода являются приемлемое время ввода значений функции и время собственно минимизации функции. Однако не следует смотреть на проблему минимизации слишком пессимистично, т.к. известно, что реальные булевы функции большого числа аргументов в подавляющем большинстве случаев не определены, причем число неопределенных наборов возрастает с ростом числа аргументов булевой функции.
Синтез комбинационных схем.
Существует класс логических устройств, у которых выходные сигналы схемы в данный момент времени зависят только от комбинации входных сигналов поступивших на схему в данный момент времени: