Файл: Е. А. Рябухина, О. А. Гущина, Д. А. Губанов, Д. В. Емельянов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 112
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример выполнения задания
Условие: составить программу для вычисления значения функции y=f(x)=x2+4x-ex при изменении x от 0 до 1 с шагом h. Подсчитать количество положительных, отрицательных и нулевых значений функции.
Программный код:
SUBlab4()
Dim k1 As Byte, k2 As Byte, k3 As Byte, i As Byte
Dim f As Single, x As Single, h As Single
k1=0
k2=0
k3=0
I=1
For x=0 To 1 Step h
f=x^2+4*x-exp(x)
If f>0
Then k1=k1+1
Else
If f=0 Then k2=k2+1 Else k3=k3+1
Cells(I,1)=Format(f,”00.00”)
i=i+1
Next x
ActiveSheet.range(“C1:E1”).select
With selection
.merge
.Font.bold=true
.Font.italic=true
.font.size=14
.font.name=”Times New Roman”
.borders.color=RGB(100,0,100)
End With
Selection=”K1=”&str(k1)
ActiveSheet.range(“C2:E2”).select
With selection
.merge
.Font.bold=true
.Font.italic=true
.font.size=14
.font.name=”Times New Roman”
.borders.color=RGB(70,50,100)
End With
Selection=”K2=”&str(k2)
ActiveSheet.range(“C3:E3”).select
With selection
.merge
.Font.bold=true
.Font.italic=true
.font.size=14
.font.name=”Times New Roman”
.borders.color=RGB(0,100,100)
End With
Selection=”K3=”&str(k3)
EndSUB
ЛАБОРАТОРНАЯ РАБОТА № 5.
«Программирование циклических алгоритмов с определенным числом повторений с условным оператором в теле цикла»
Цель работы: изучение различных конструкций условного оператора, размещающегося внутри цикла.
Задание: составить программу для вычисления всех корней уравнения ax2+bx+c=0, в котором параметр a=a(t) изменяется по закону, указанному в табл. 12.
Таблица 12
| Вариант | a(t) | Отрезок изменения t | Шаг | Const |
| 1 | t2 – t + 1 | [0; 1] | 0,1 | b = -2; c = 1 |
| 2 | 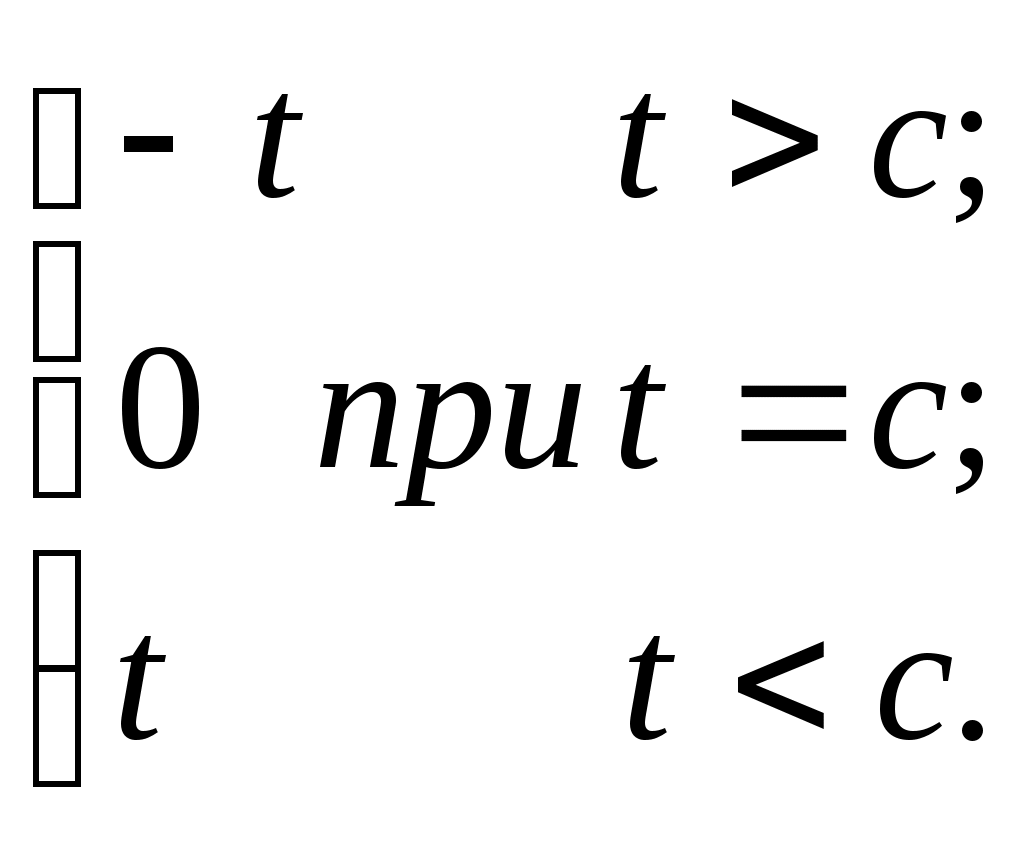 | [0; 3] | 0,3 | b = 3; c = 6 |
| 3 | ln(t + 0,1) | [0; 1,9] | 0,2 | b = 8; c = 9 |
| 4 | 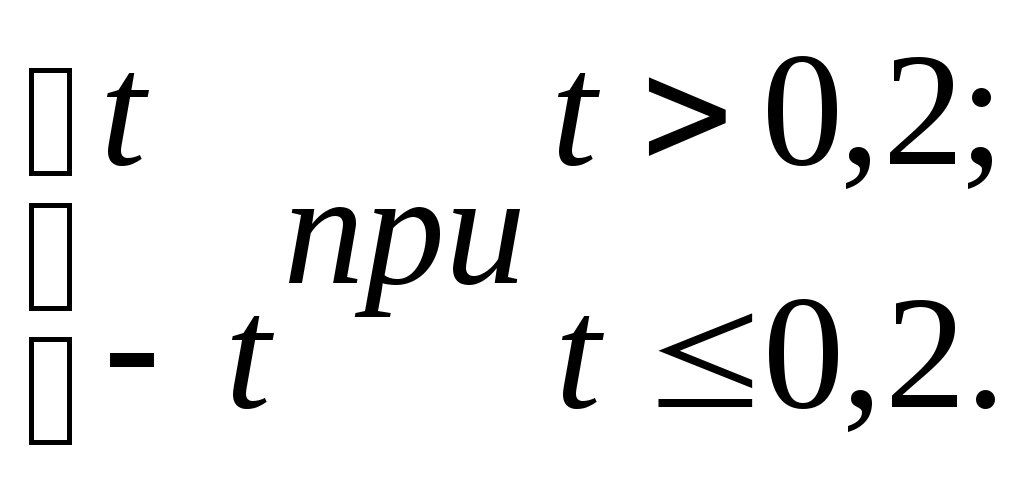 | [0; 1] | 0,1 | b = 0,24; c = 0,14 |
| 5 | 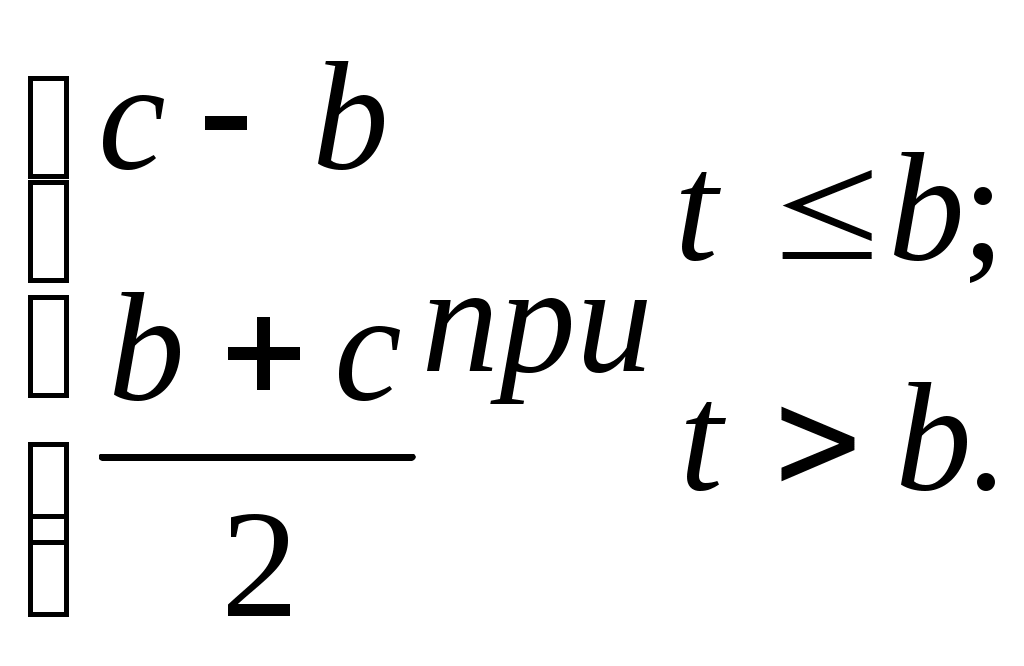 | [0; 2] | 0,2 | b = 1; c = 2 |
| 6 | 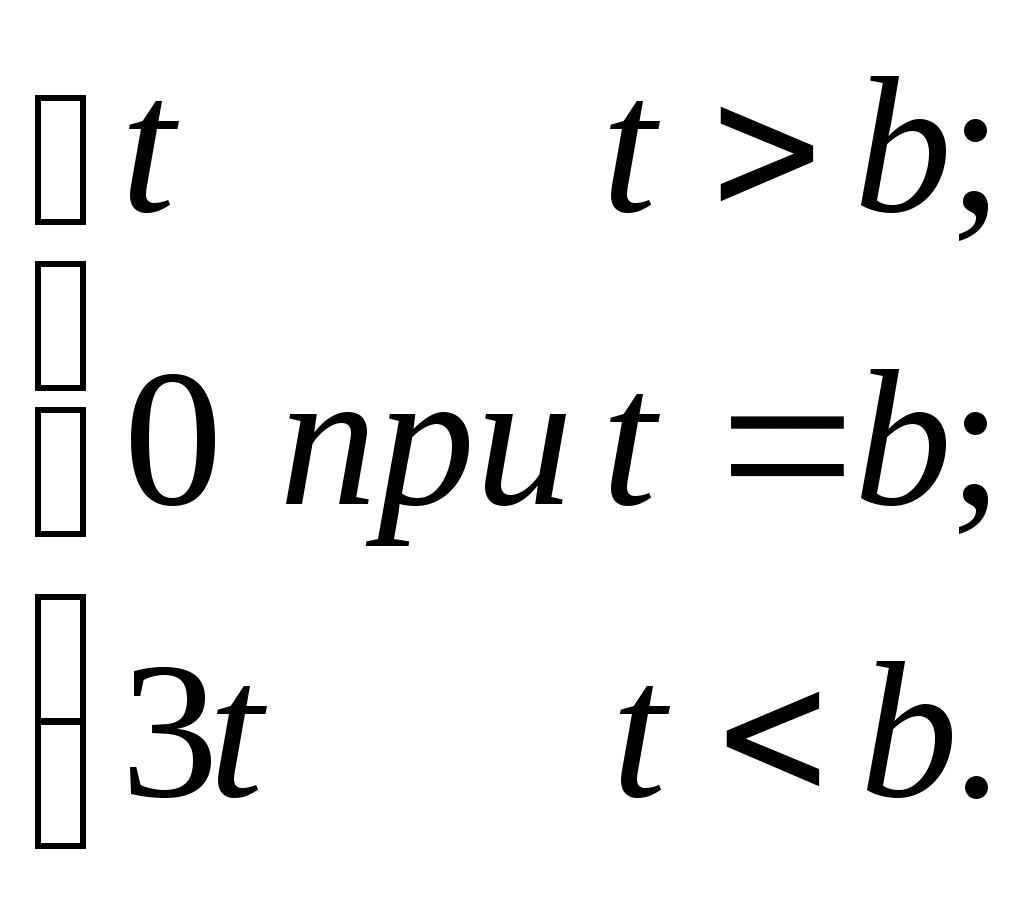 | [0; 2,1] | 0,3 | b = 1,45; c = -2,2 |
| 7 | cos(t) + 0,2 | [0;] | /10 | = 3,1415926; b = -0,2; c = 0,344 |
| 8 | 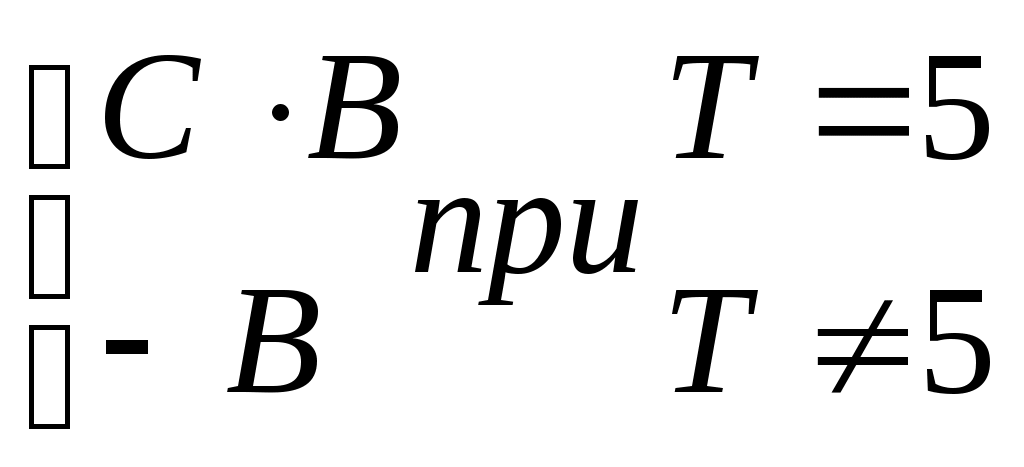 | [2; 8] | 0,5 | b = 1; c = 2 |
| 9 | 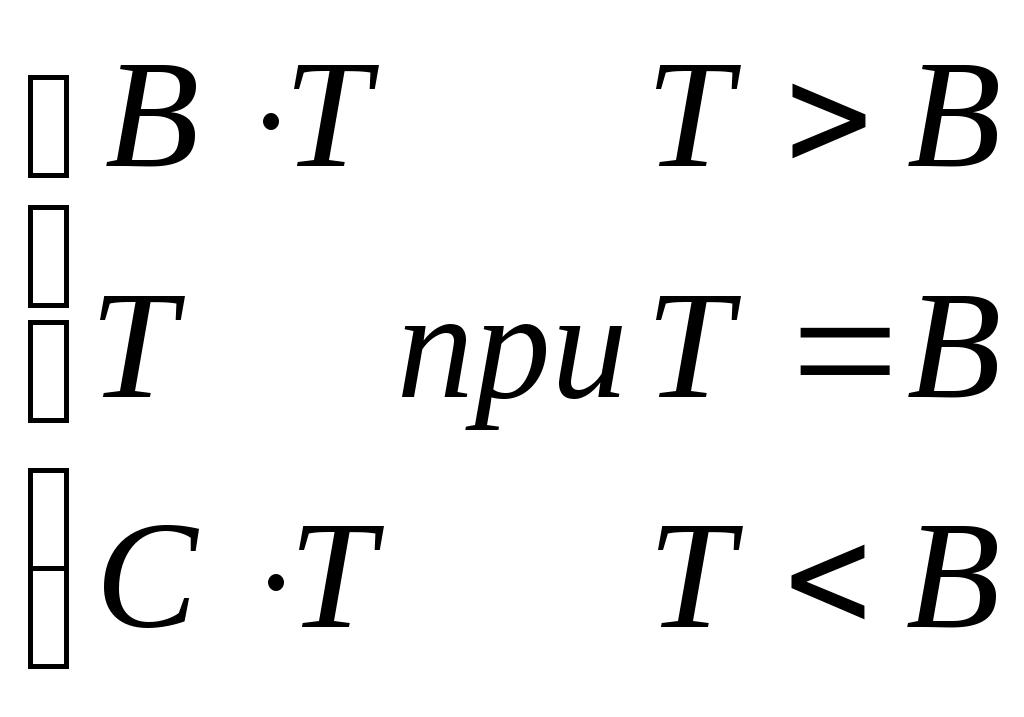 | [1; 9] | 0,1 | b = 5; c = 2 |
| 10 | eT – 2 | [0,2;] | 0,2 | b = 3; c = 5 |
Пример выполнения задания
Условие: составить программу для вычисления всех корней уравнения ax2+bx+c=0, в котором параметр a= a(t)= sin(t), отрезок изменения t: [0; 1], шаг изменения tравен 0.1; b= 3; b= 1.
Программный код:
SUBlab5()
Dim i As Byte
Dim d As Single, x1 As Single, x2 As Single, a As Single, b As Single, c As Single, t As Single
i=1: c=1: b=3: h=0.1
For t=0 To 1 Step h
a=sin(t)
d=b^2-4*a*c
If d>=0
Then
x1=(-b+sqr(d))/(2*a)
x2=(-b-sqr(d))/(2*a)
Cells(i,1)=x1
Cells(i,2)=x2
Else Cells(i,1)=”Корнейнет”
End If
i=i+1
Next t
ActiveSheet.range(“A1:B11”).select
With selection
.Font.bold=true
.Font.italic=true
.font.size=14
.font.name=”Times New Roman”
.bord2ers.color=RGB(100,0,100)
End With
End SUB
ЛАБОРАТОРНАЯ РАБОТА №6.
«Табуляции функции. Нахождение минимального/максимального значения функции на заданном интервале»
Цель работы: изучение стандартных алгоритмов максимума и минимума.
Задание: составить программу для вывода на печать значения функции с циклически изменяющимся аргументом; определить ее минимум или максимум согласно варианту (табл. 13).
Таблица 13
| Вариант | F(x) | n | a | b | t1 | t2 | t3 | Экстремум |
| 1 | | 10 | 0 | 2 | 3.2 | 4.1 | 5.467 | max |
| 2 | | 12 | 1 | 3.2 | 2.4 | | | min |
| 3 | | 10 | 0.2 | 0.8 | 2.3 | -3 | 4.2 | max |
| 4 | | 15 | 1 | 1.4 | 5.1 | 6.2 | 7.1 | min |
| 5 | | 10 | 2 | 3.1 | 2.2 | 2.3 | 4.2 | max |
| 6 | | 10 | 2 | 3.456 | 6.248 | -4.744 | 2.3 | max |
| 7 | | 12 | 1 | 2 | 6.2 | -3.42 | 5.2 | min |
| 8 | | 10 | 0.7 | 2.2 | -1 | -2 | 3.4 | max |
| 9 | | 16 | 0.1 | 1 | 0.001 | 0.2 | 0.3 | min |
| 10 | | 10 | 2 | 3 | 10.45 | 6.4 | 2.3 | max |
| 11 | | 15 | 2.2 | 3.3 | 5.48 | 6.2 | 7.3 | min |
| 12 | 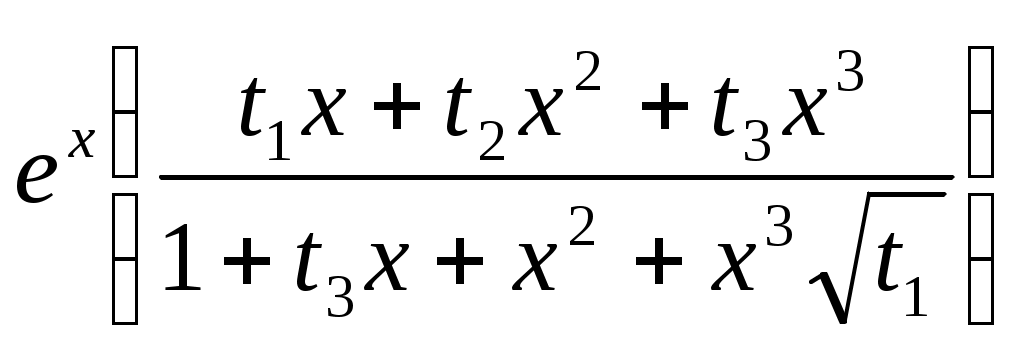 | 10 | 0 | 1 | 2.2 | 3.1 | 4.5 | max |
| 13 | | 8 | 1 | 2 | 3.2 | 3.4 | 5.94391 | min |
| 14 | | 12 | 2 | 3 | 4.67 | 5.3 | 0.9 | min |
| 15 | | 11 | 2 | 4 | 2.2 | 3.12 | 1.8 | max |
| 16 | | 9 | 2 | 2.9 | 4 | 2.3 | 2.658 | min |
| 17 | | 14 | -1 | 0 | 6.548 | 0.5 | -3.48 | max |
| 18 | | 13 | 10 | 20 | 3.48 | 6.25 | -3.14 | min |
| | | | | | | | | |
| | | | | | | | Окончание табл.13 | |
| 19 | | 16 | 0 | 1 | 0.2 | 2.4 | 4.231 | min |
| 20 | | 9 | 0 | 1 | 10 | 13.64 | 1.3 | max |
Примеры выполнения заданий
Условие: составить программу для вывода на печать значения функции с циклически изменяющимся аргументом; определить ее максимум.
Программный код:
SUBlab6()
Dim a As Single, b As Single, f As Single, x As Single, max As Single, h As Single, n As Byte, I As Byte
I=1: a=1: b=3: n=15
T1!=0.34: t2!=0.56: t3!=1.389
Max=-100: h=(b-a)/n
For x=a To b Step h
F=(x^2+t1*x+exp(x))/(t2*x-sqr(x))-t3
Cells(I,1)=Format(x,”00.00”)
Cells(I,2)=Format(f,”00.000”)
If f>max Then max=f
Next x
ActiveSheet.range(“A17:C17”).select
With selection
.Font.bold=true
.Font.italic=true
.font.size=14
.font.name=”Times New Roman”
.borders.color=RGB(100,0,100)
End With
Selection=”max=”&Format(max, ”00.000”)
End SUB
ЛАБОРАТОРНАЯ РАБОТА № 7.
«Формирование матриц»
Цель работы: разработка, отладка и тестирование программ для ввода/вывода и обработки массивов.
Задание: сформировать элементы массива А размерностью 5×5 по формулам, указанным в табл. 14.
Таблица 14
| Вариант | Формула | | Вариант | Формула |
| 1 | Aij = i+ j. | | 9 | 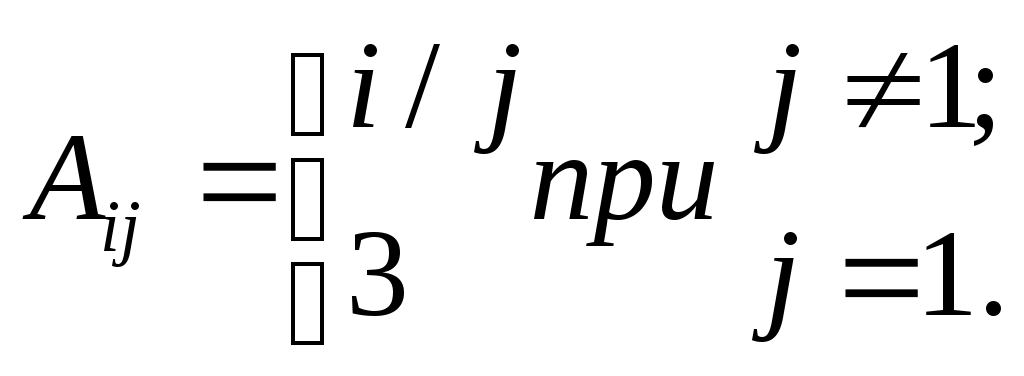 |
| 2 | 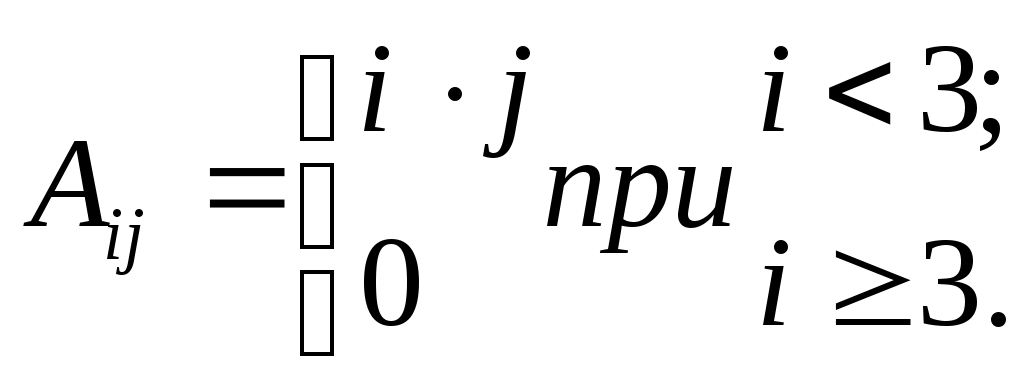 | | 10 | Aij = 2(i – j). |
| 3 | 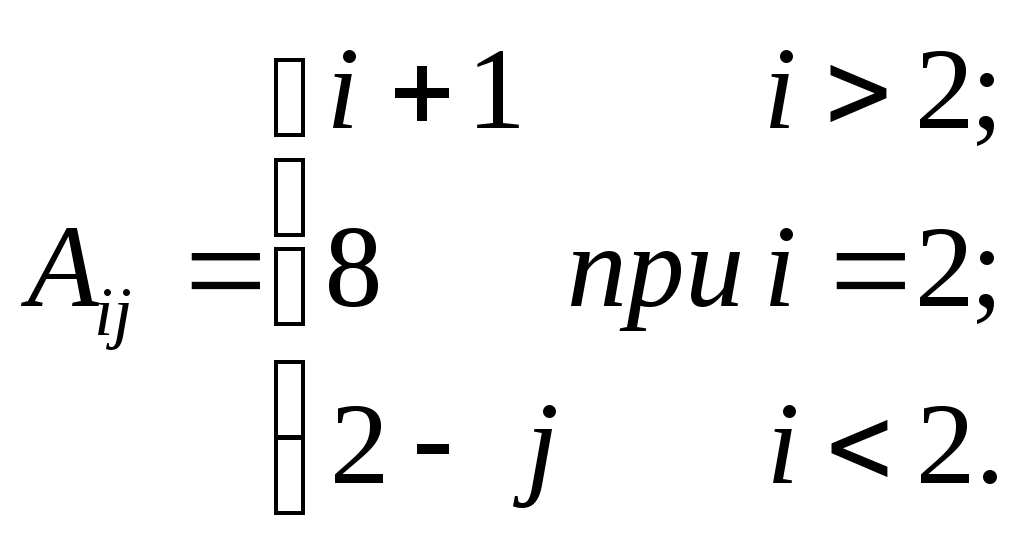 | | 11 | 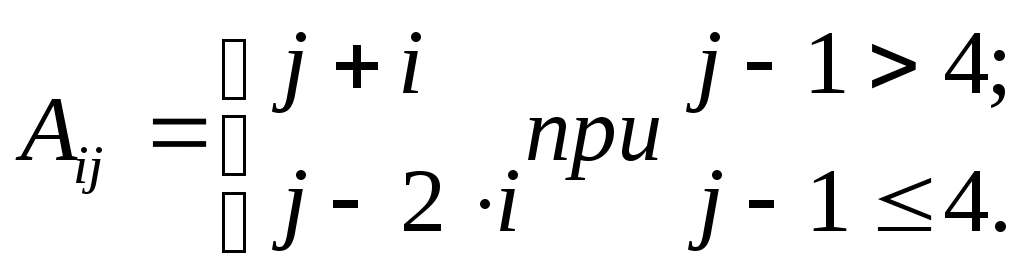 |
| 4 | 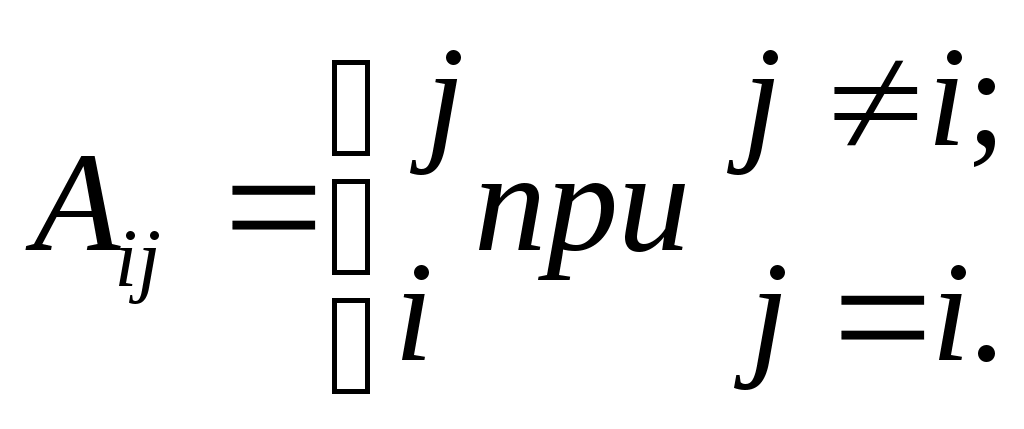 | | 12 | 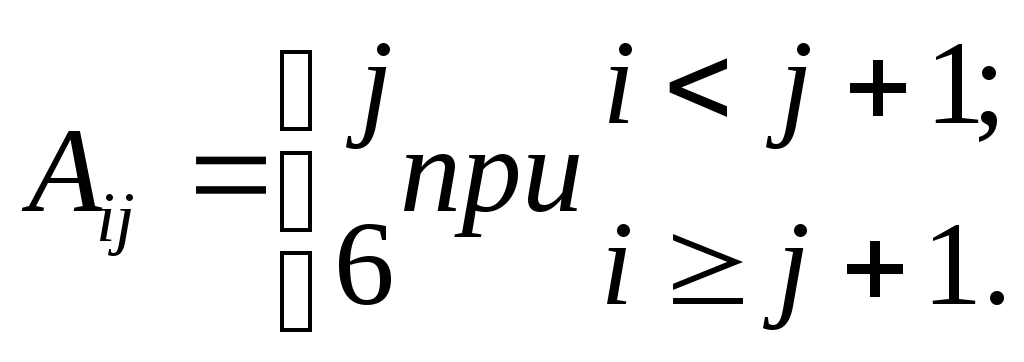 |
| 5 | 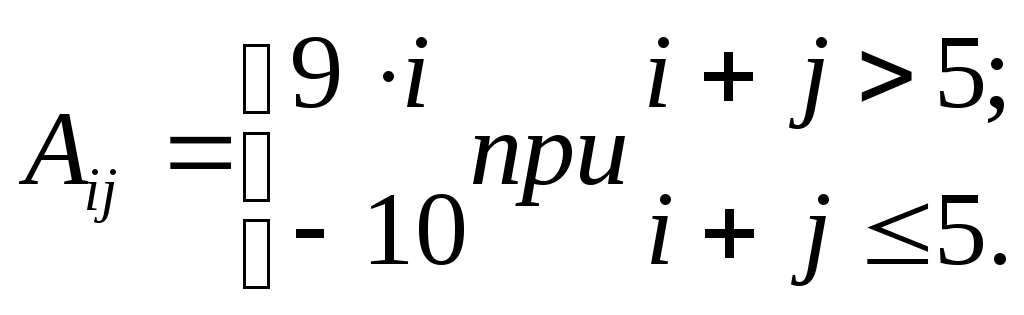 | | 13 | 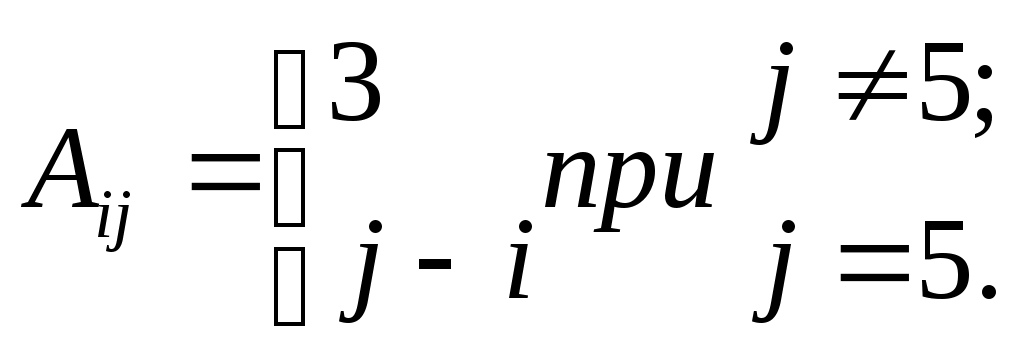 |
| 6 | 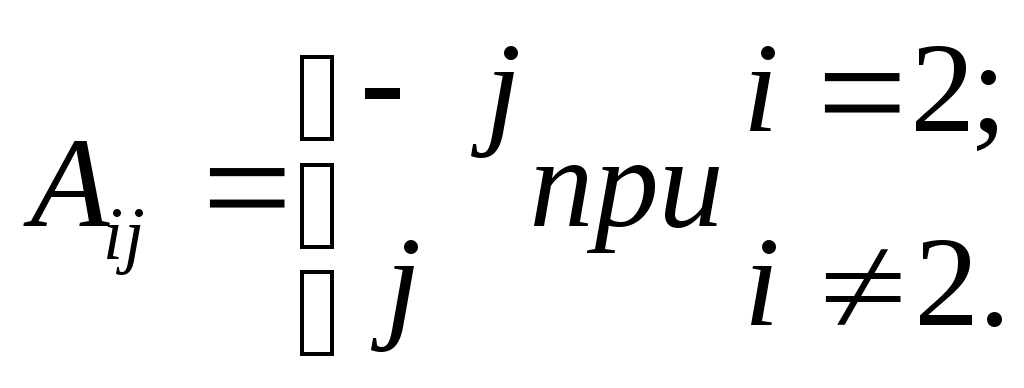 | | 14 | 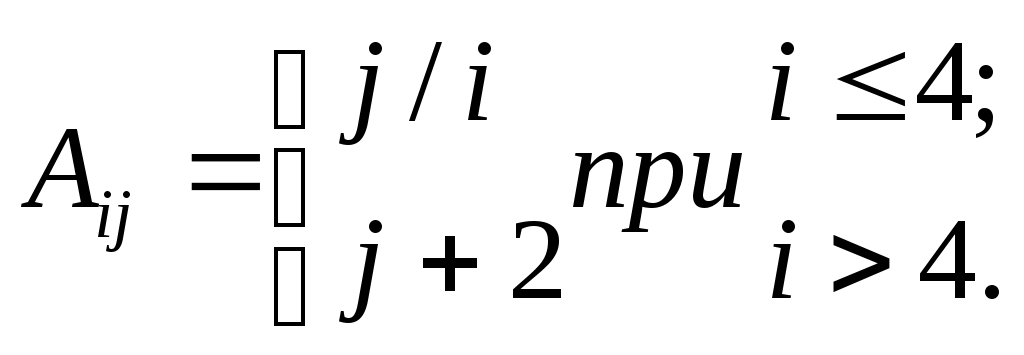 |
| 7 | 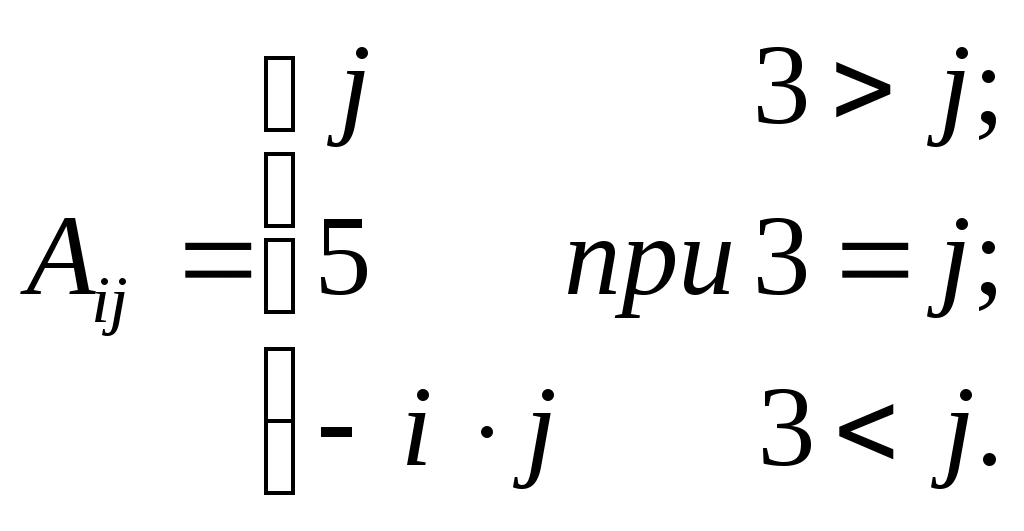 | | 15 | 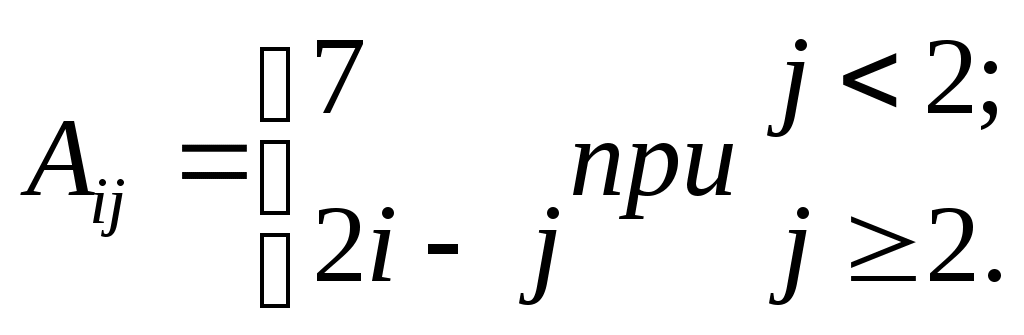 |
| 8 | 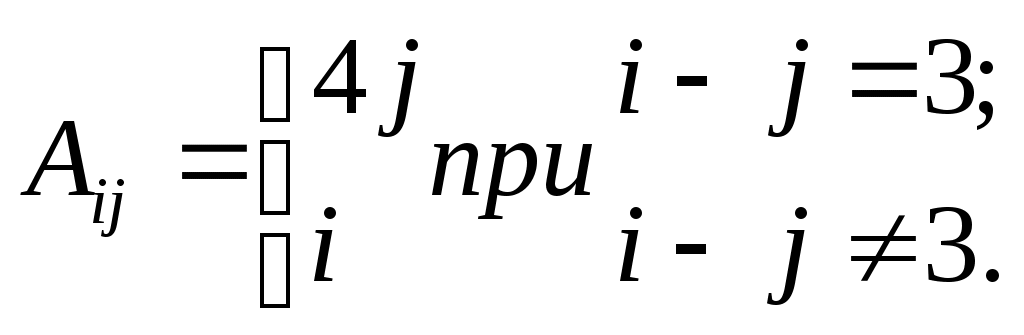 | | 16 | 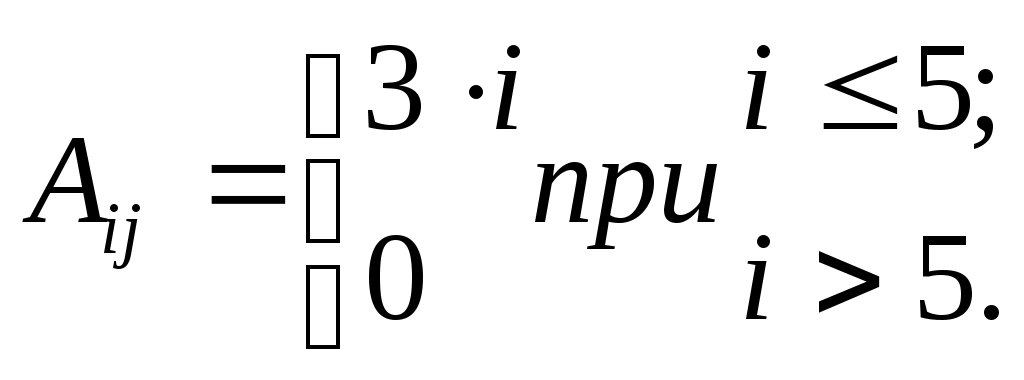 |