Задача № 1

В вертикальном цилиндрическом резервуаре типа РВС номинальной емкости V хранится М нефтепродукта плотностью ₂₀. Определить колебание уровня нефтепродукта в резервуаре, если его температура изменилась от t₁ до t₂ . Расширение резервуара не учитывать.

Дано:

V = 100 м³;

М = 70 тн

₂₀ = 750 кг/м³;

t₁ = 30 ⁰С;

t₂ = 0⁰С.

Найти:



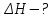
Решение:

Диаметр резервуара равен 4,73 м, высота 5,96 м.

Масса нефтепродукта определяется по формуле:



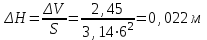
где V₁, V₂ – объем нефтепродукта при заданной температуре, м³;

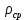
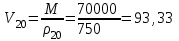– средняя плотность нефтепродукта при заданной температуре изменения уровня, кг/м³.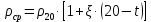



г 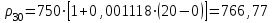де 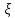– коэффициент объемного расширения (при заданной плотности = 0,000831 1/C)

Изменение объема нефтепродукта при изменении температуры:



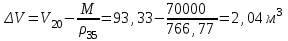
Колебание уровня нефтепродукта в резервуаре:



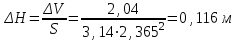
Ответ: Колебания уровня нефтепродукта в резервуаре составляет 0,116 м

Задача № 3
Определить пропускную способность самотеч­ного трубопровода диаметром D_н х  мм и длиной L км при разности нивелирных отметок начальной и конечной точек трубо­провода Z, м.

Дано:

D_н = 159 мм = 0,159 м;

δ = 4 мм = 0,004 м;

L = 1км = 1000 м;

ΔZ = 10 м;

v= 7∙10^-6 м²/с;

ρ₂₀ = 850 кг/м³

Найти:

Q = ?

Решение:

Напишем уравнение Бернулли относительно плоскости сравнения 0–0, взятой по оси симметрии трубы на выходе жидкости из трубопровода, для сечений

---

1–1 (уровень жидкости в резервуаре) и 2–2 (выход жидкости из трубопровода).



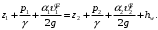
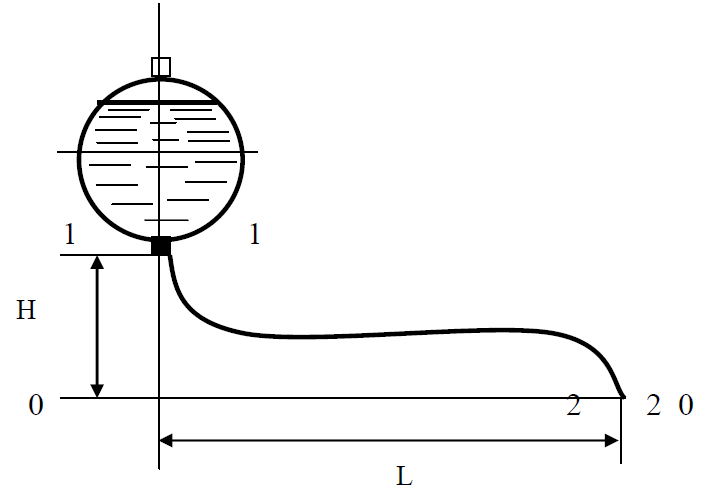
Сечения 1–1 и 2–2 выбраны потому, что давление в них известно и оно равно атмосферному р_ат, следовательно

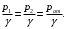
Скорость движения жидкости в резервуаре ϑ₁ при достаточно больших его размерах по сравнению с выходным отверстием трубы можно считать близкой к нулю (ϑ₁ ≈ 0), а значит,

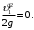
Координата сечения 1–1 над плоскостью сравнения z₁= h, а сечения 2–2 z₂= 0, так как плоскость сравнения 0–0 проходит по оси симметрии трубы.

Принимаем α₂ = 1, так как при турбулентном режиме α₂ = 1,05÷1,10.

С учетом выше изложенного уравнение Бернулли принимает следующий вид:



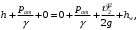
или после сокращения получаем



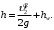
В связи с тем, что про местные потери напора в трубопроводе ничего не сказано, принимаем их равными 10% от потерь напора по длине. Тогда величину потерь напора h_wопределим из выражения



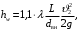
где d_вн – внутренний диаметр трубы, определяемый из выражения

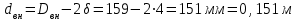
При этом коэффициент сопротивления трения, с допущением того, что данная стальная труба эксплуатируется несколько лет, приближенно принимаем равным λ = 0,02



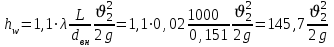
Подставив данное значение в преобразованное уравнение Бернулли, получаем:



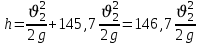
Из полученного выражения определим скорость:

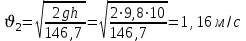
Зная скорость движения жидкости на выходе из трубы, уточним, правильно ли мы приняли λ = 0,02.

Определим число Рейнольдса из выражения

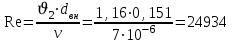
Из полученного числа Рейнольдса следует, что режим движения турбулентный. Определим, по какой формуле необходимо рассчитывать коэффициент

---

λ.

Предположив, что это переходная область турбулентного режима, произведем проверку, при этом Δ_экак для бывших в употреблении бесшовных стальных труб определим из таблицы, Δ_э= 0,2 мм


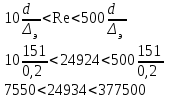
Так как неравенство выдерживается, то производим расчет коэффициента трения λ по формуле Альтшуля


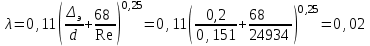
Так как коэффициенты трения λ расчетный и принятый нами полностью совпали, то уточнять скорость нет необходимости.

Поэтому определяем расход из выражения


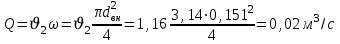
Ответ: Q = 0,02 м³ /с.

Задача № 4

Определить расход нефтепродукта в трубопро­воде диаметром D_н х  и длиной L , если кинематическая вязкость нефтепродукта , плотность , а перепад дав­ления в трубопроводе равен Р.

Дано:

D_н = 426 мм = 0,426 м;

δ = 7 мм = 0,007 м;

L = 2,5 км = 2500 м;

Δр = 0,04 МПа =40000 Па;

v = 0, 5∙10^-4 м²/с =5∙10^-6 м²/с;

ρ₂₀ = 820 кг/м³

Найти:

Q = ?

Решение:

Напишем уравнение Бернулли относительно плоскости сравнения 0–0, взятой по оси симметрии трубы на выходе жидкости из трубопровода, для сечений 1–1 (уровень жидкости в резервуаре) и 2–2 (выход жидкости из трубопровода)



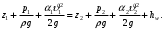
Т. к про сечения 1–1 и 2–2 ничего не известно – открытая или закрытая емкость, выход под уровень или в атмосферу, неизвестны геодезические отметки, то уравнение Бернулли перепишем в следующем виде



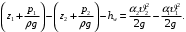
Скорость движения жидкости в резервуаре ϑ₁ при достаточно больших его размерах по сравнению с выходным отверстием трубы можно считать близкой к нулю (ϑ₁ ≈ 0), а значит,

Принимаем α₂ = 1, так как при турбулентном режиме α₂ = 1,05÷1,10.

А левую часть уравнения можно представить в виде



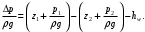
С учетом выше изложенного уравнение Бернулли принимает следующий вид:

---

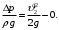
или после сокращения и преобразования получаем



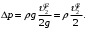
Из полученного выражения определим скорость



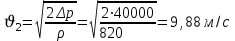
Расход определяем из выражения



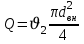
А внутренний диаметр трубы, из зависимости



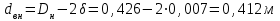
Подставив цифровые значения окончательно получаем



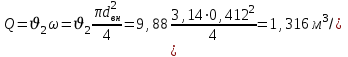
Ответ: Q = 1,316 м³ /с.
Задача № 8

Определить время слива нефтепродукта из цистерны грузоподъемностью N через универсальный сливной прибор, трубопровод имеет длину L , диаметр D_н и вы­соту Н, температура слива t⁰С. Схема слива приведена на рис. 4. Вязкость нефтепродукта ₂₀ и _50. Местные сопротивления: универсальный сливной при­бор, плавный переход, задвижка, два угольника.

Дано:

N = 50 м³;

L = 15 м;

D_н = 159 мм = 0,159 м;

δ = 4 мм = 0,004 м;

Н = 1,9 м;

t = 25 °С;

v₂₀ = 34∙10^-4 м²/с;

v₅₀ = 2,1∙10^-4 м²/с = 210∙10^-6 м²/с

Найти:

t_слива= ?


Решение:

В нашем случае, т. к. ничего не известно про емкость предполагаем, что она открыта, т.е. давление на поверхности р_ат, высотой жидкости в емкости пренебрегаем.

Т. е. при этих допущениях мы получаем максимальное время слива.

Плоскость сравнения 0–0 проведем через место вытекания жидкости в атмосферу.

Напишем уравнение Бернулли для сечений 1–1 сливное отверстие резервуара и 2–2 выход жидкости в атмосферу из трубопровода.



Соотнесем полученное уравнение с нашими данными:



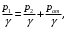
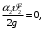т. к. считаем, резервуар достаточно большим по объему (60 м³) и соответственно ϑ₁ ≈ 0;

z₁ = H , z₂ = 0, принимаем α₂ = 2, предполагая ламинарный режим движения жидкости (из-за относительно высокой вязкости).

---

С учетом вышеизложенного уравнение Бернулли принимает следующий вид:



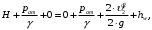
или после сокращения получаем



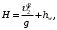
Определяем неизвестные показатели выражения:

– скорость жидкости ϑ₂ на выходе из трубы в первом приближении согласно рекомендаций приложения 4.3, принимаем равной 0,357 м/с.

Тогда расход определим из выражения



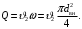
Причем внутренний диаметр трубы определим из выражения



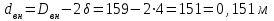
Тогда



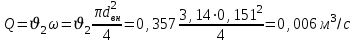
– величину потерь напора h_wв трубопроводе определяем как суммарные потери, состоящие из потерь напора по длине h_{w ℓ}и местных потерь напора h_wм



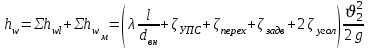
где ζ_УСП– коэффициент местного сопротивления универсального сливного прибора;

ζ_перех– коэффициент местного сопротивления при плавном переходе;

ζ_задв – коэффициент местного сопротивления задвижки;

ζ_угол– коэффициент местного сопротивления угольника с углом поворота 90⁰.

Для определения коэффициента λ предварительно определим число Рейнольдса из выражения



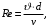
при этом коэффициент кинематической вязкости определим используя выражения 1.1 и 1.2 методических указаний.

Основная расчетная зависимость:



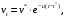
где v_t – вязкость при температуре t, м²/с; v^* – вязкость при известной температуре t^*, м²/с; t – температура нефтепродукта, °С; u – показатель крутизны вискограммы, 1/°С.

Причем



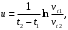
где v_t1– вязкость при температуре t₁; м²/с; v_t2 – вязкость при температуре t₂, м²/с.

---

Смотрите также файлы

• статистика. Комбинаторика блімі бойынша жиынты баалау 1нса 1.docx

• Практическая работа по дисциплине Основы электроснабжения железных дорог на тему Расчёт системы электроснабжения.docx

• Закрепила уже сложившуюся к тому времени систему высших органов государственной власти 1) Всероссийский съезд Советов 2) избираемый Съездом Всероссийский Центральный Исполнительный Комитет Советов (вцик советов).docx

• 6. 2А Заттар жне материалдар блімі бойынша жиынты баалау Жаратылыстану пні бойынша 6 сынып.docx

• Переменный ток.docx