Добавлен: 02.12.2023
Просмотров: 66
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; 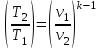 ;
;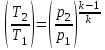 ,
,
можно получить приведенные соотношения для работы расширения в адиабатном процессе:
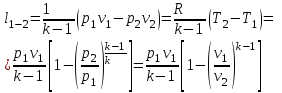 (23)
(23)
В адиабатном процессе не происходит теплообмена рабочего тела с окружающими системами . Из первого закона термодинамики следует, что работа совершается только за счет изменения внутренней энергии:
. Из первого закона термодинамики следует, что работа совершается только за счет изменения внутренней энергии:
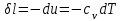 (24)
(24)
При для двух значений температур (
для двух значений температур ( и
и  ):
): 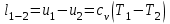 (25)
(25)
Изменение энтропии в адиабатном процессе: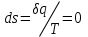 (26)
(26)
Энтропия является величиной постоянной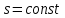 .
.
1.5. Политропный процесс
Политропный процесс – термодинамический процесс изменения состояния физической системы, в течение которого сохраняется постоянство теплоемкости.
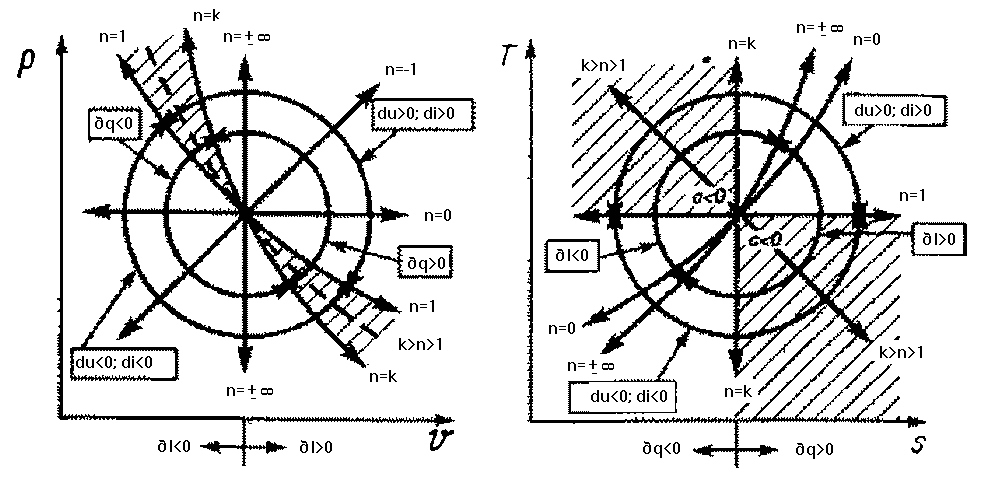
Рис.1.5 Сводные графики политропных процессов
Уравнение политропного процесса имеет вид: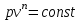 .
.
Давления обратно пропорциональны объемам в степени :
: 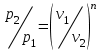 (27)
(27)
Коэффициент политропы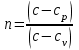 считается для отдельно взятого процесса величиной постоянной
считается для отдельно взятого процесса величиной постоянной 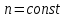 значение которой могут изменятся
значение которой могут изменятся 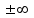 .
.
При известный параметрах состояния: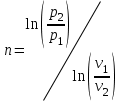 (28)
(28)
Работа расширения в политропном процессе:
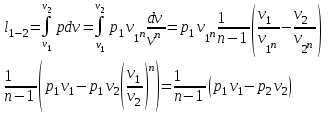
(29)
Используя уравнение состояния и соотношения:
и соотношения:
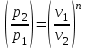 ;
; 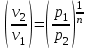 ;
; 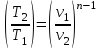 ;
;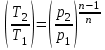 ,
,
можно получить приведенные соотношения для работы расширения в адиабатном процессе:
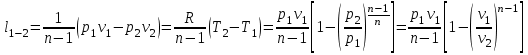 (30)
(30)
Изменение внутренней энергии в политропном процессе: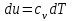 (31)
(31)
При для двух значений температур (
для двух значений температур ( и
и  ):
): 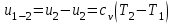 (32)
(32)
Изменение энтальпии в политропном процессе: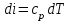 (33)
(33)
При для двух значений температур (
для двух значений температур ( и
и  ):
): 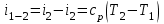 (34)
(34)
Количество теплоты в политропном процессе: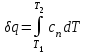 (35)
(35)
При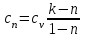 и для двух значений температур (
и для двух значений температур ( и
и  ):
): 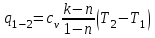 (36)
(36)
Изменение энтропии в политропном процессе: (37)
(37)
Энтропия в политропном процессе определится по зависимости: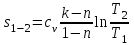 (38)
(38)
Политропный процесс обобщает всю совокупность основных термодинамических процессов.
2. Практическая часть.
2.1. Исходные данные для расчета
Вариант задания №13
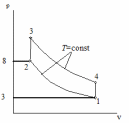
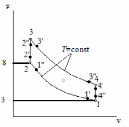
Рис. 2.1 Рабочая диаграмма процесса
Цикл состоит из 4 процессов:
1 – 2 изотермический процесс;
2 – 3 изохорный процесс;
3 – 4 изотермический процесс;
4 – 1 изохорный процесс;
Исходными данными для расчета являются следующие значения термодинамических параметров в точках:p1=3 атм; p2=8 атм; t1=27C;t3=200C. Теплоемкости процессов: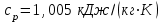 ;
; 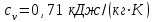 . Удельная газовая постоянная воздуха
. Удельная газовая постоянная воздуха 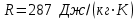 .
.
2.2. Порядок выполнения расчетов
Переведём единицы измерения в систему СИ:
1 атм 98 кПа;
p1 = 3 атм = 3,03105 Па;
p2 = 8 атм =8,1105 Па;
T1=300 K.
T3=473 K.
2.3. Определяем параметры состояния p, v, T, u, i для основных точек цикла:
Для точки 1 дано p1=3,03105 Па, T1=300 K.
Из уравнения Клапейрона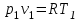 следует, что
следует, что
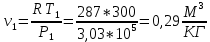
Находим внутреннюю энергию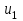 и энтальпию
и энтальпию 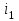 при температуре T1=300 K:
при температуре T1=300 K:
u1=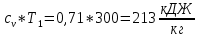
i1=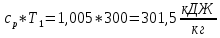
Для точки 2 дано T1=T2=300 K, p2 = 8,1105 Па.
Для определения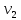
воспользуемся отношением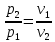 :
:
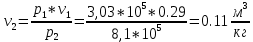
Находим внутреннюю энергию u2 и энтальпиюi2 при температуре T2=300 K.
u2=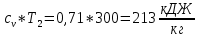
i2=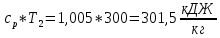
Для точки 3 дано T3=473 K,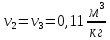
Используя соотношение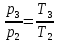 можем найти p3:
можем найти p3:
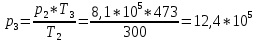 Па.
Па.
Находим внутреннюю энергию u3 и энтальпиюi3 при температуре T3=473 K.
u3=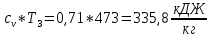
i3=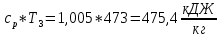
Для точки 4 дано T3=T4=473 К,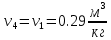
Из отношения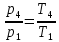 можем найти p4:
можем найти p4:
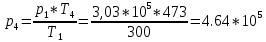 Па
Па
Находим внутреннюю энергию u4 и энтальпиюi4 при температуре T4=473 K.
u4=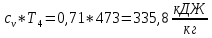
i4=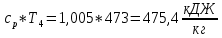
2.4. Определение параметров p, v, T, u, i для дополнительных точек цикла:
Для точки 1' дано T1=T1’=300 К, v1’=0,27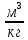 .Определим p1’, u1’, i1’.
.Определим p1’, u1’, i1’.
Из отношения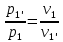 можем определить p1’:
можем определить p1’:
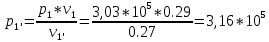 Па
Па
Находим внутреннюю энергию u1’ и энтальпию i1’ при температуре T1’=300 K
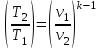 ;
;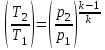 ,
,можно получить приведенные соотношения для работы расширения в адиабатном процессе:
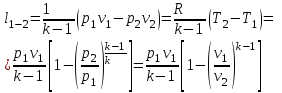 (23)
(23)В адиабатном процессе не происходит теплообмена рабочего тела с окружающими системами
 . Из первого закона термодинамики следует, что работа совершается только за счет изменения внутренней энергии:
. Из первого закона термодинамики следует, что работа совершается только за счет изменения внутренней энергии: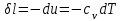 (24)
(24)При
 для двух значений температур (
для двух значений температур ( и
и  ):
): 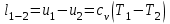 (25)
(25)Изменение энтропии в адиабатном процессе:
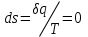 (26)
(26)Энтропия является величиной постоянной
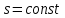 .
.1.5. Политропный процесс
Политропный процесс – термодинамический процесс изменения состояния физической системы, в течение которого сохраняется постоянство теплоемкости.

Рис.1.5 Сводные графики политропных процессов
Уравнение политропного процесса имеет вид:
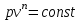 .
.Давления обратно пропорциональны объемам в степени
 :
: 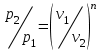 (27)
(27)Коэффициент политропы
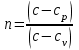 считается для отдельно взятого процесса величиной постоянной
считается для отдельно взятого процесса величиной постоянной 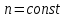 значение которой могут изменятся
значение которой могут изменятся 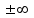 .
.При известный параметрах состояния:
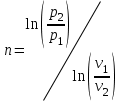 (28)
(28)Работа расширения в политропном процессе:
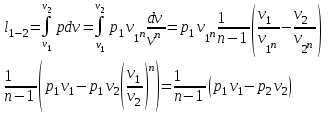
(29)
Используя уравнение состояния
 и соотношения:
и соотношения: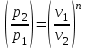 ;
; 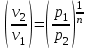 ;
; 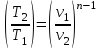 ;
;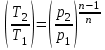 ,
,можно получить приведенные соотношения для работы расширения в адиабатном процессе:
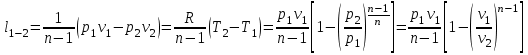 (30)
(30)Изменение внутренней энергии в политропном процессе:
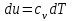 (31)
(31)При
 для двух значений температур (
для двух значений температур ( и
и  ):
): 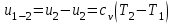 (32)
(32)Изменение энтальпии в политропном процессе:
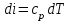 (33)
(33)При
 для двух значений температур (
для двух значений температур ( и
и  ):
): 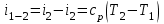 (34)
(34)Количество теплоты в политропном процессе:
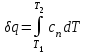 (35)
(35)При
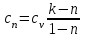 и для двух значений температур (
и для двух значений температур ( и
и  ):
): 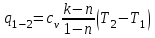 (36)
(36)Изменение энтропии в политропном процессе:
 (37)
(37)Энтропия в политропном процессе определится по зависимости:
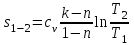 (38)
(38)Политропный процесс обобщает всю совокупность основных термодинамических процессов.
| Процесс | 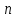 | 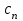 |
| изохорный 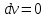 | 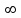 | 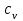 |
| изобарный 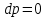 | 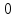 | 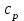 |
| изотермический  | 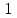 | 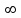 |
| адиабатный 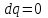 |  | 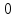 |
2. Практическая часть.
2.1. Исходные данные для расчета
Вариант задания №13


Рис. 2.1 Рабочая диаграмма процесса
Цикл состоит из 4 процессов:
1 – 2 изотермический процесс;
2 – 3 изохорный процесс;
3 – 4 изотермический процесс;
4 – 1 изохорный процесс;
Исходными данными для расчета являются следующие значения термодинамических параметров в точках:p1=3 атм; p2=8 атм; t1=27C;t3=200C. Теплоемкости процессов:
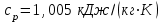 ;
; 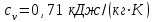 . Удельная газовая постоянная воздуха
. Удельная газовая постоянная воздуха 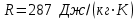 .
.2.2. Порядок выполнения расчетов
Переведём единицы измерения в систему СИ:
1 атм 98 кПа;
p1 = 3 атм = 3,03105 Па;
p2 = 8 атм =8,1105 Па;
T1=300 K.
T3=473 K.
2.3. Определяем параметры состояния p, v, T, u, i для основных точек цикла:
Для точки 1 дано p1=3,03105 Па, T1=300 K.
Из уравнения Клапейрона
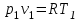 следует, что
следует, что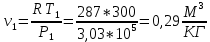
Находим внутреннюю энергию
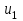 и энтальпию
и энтальпию 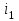 при температуре T1=300 K:
при температуре T1=300 K:u1=
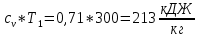
i1=
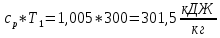
Для точки 2 дано T1=T2=300 K, p2 = 8,1105 Па.
Для определения
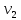
воспользуемся отношением
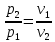 :
: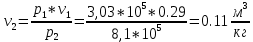
Находим внутреннюю энергию u2 и энтальпиюi2 при температуре T2=300 K.
u2=
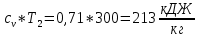
i2=
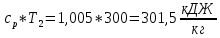
Для точки 3 дано T3=473 K,
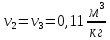
Используя соотношение
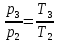 можем найти p3:
можем найти p3: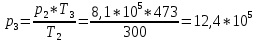 Па.
Па.Находим внутреннюю энергию u3 и энтальпиюi3 при температуре T3=473 K.
u3=
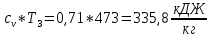
i3=
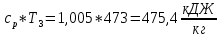
Для точки 4 дано T3=T4=473 К,
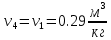
Из отношения
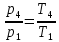 можем найти p4:
можем найти p4: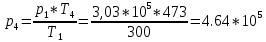 Па
ПаНаходим внутреннюю энергию u4 и энтальпиюi4 при температуре T4=473 K.
u4=
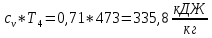
i4=
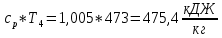
2.4. Определение параметров p, v, T, u, i для дополнительных точек цикла:
Для точки 1' дано T1=T1’=300 К, v1’=0,27
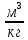 .Определим p1’, u1’, i1’.
.Определим p1’, u1’, i1’.Из отношения
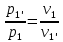 можем определить p1’:
можем определить p1’: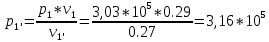 Па
ПаНаходим внутреннюю энергию u1’ и энтальпию i1’ при температуре T1’=300 K