Файл: Целью работы является анализ преобразований Лапласа.doc

Оглавление

Введение

Преобразова́ние Лапла́са (ℒ) — интегральное преобразование, связывающее функцию {\displaystyle \ F(s)}\ F(s) комплексного переменного (изображение) с функцией {\displaystyle \ f(x)}\ f(x) вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Целью работы является анализ преобразований Лапласа.

Задачи работы:

- изучить теоретические основы преобразований Лапласа;

- рассмотреть практический пример.

Объект исследования – преобразования Лапласа. Предмет – математические исследования.

1 Теоретические основы преобразования Лапласа

1. Преобразование и его свойства

Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраическими уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.

В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:



При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.

---

Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением.



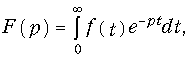
где f(t) — функция действительного переменного t, определенная при t   0 (при t < 0; f(t) = 0) и удовлетворяющая условиям ограниченного роста:



где множитель М и показатель роста с₀ — положительные действительные числа. На рис. 1 изображена область определения функции комплексного переменного F(p).

Обратное преобразование Лапласа определяют из решения (2):





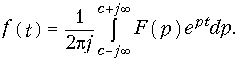
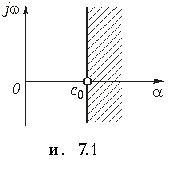
Рис.2.

Функция F(p), определяемая уравнением (2), носит название изображения по Лапласу, а функция f(t) в (4) — оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного (t) и комплексного (p) переменного, связанных преобразованием Лапласа. Для сокращенной записи преобразований (2), (4) используют следующую символику



где L - оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия   .

Рассмотрим основные свойства преобразований Лапласа.

Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме



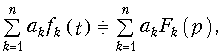
где a_k — постоянные коэффициенты разложения. Свойство (5) легко доказать, если применить к левой части соотношения (5) прямое преобразование Лапласа (2).

---

При ненулевых начальных условиях: f(0_–)¹ 0 дифференцирование оригинала соответствует следующему условию



Для доказательства (6) подставим f¢(t) в преобразование (2) в виде



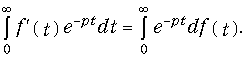
Отсюда после интегрирования по частям получаем:



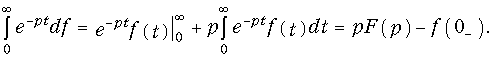
В случае нулевых начальных условий



Интегрирование оригинала



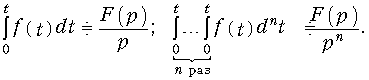
Доказательство осуществляется путем использования свойства дифференцирования оригинала (6), (7).

Изменение масштаба независимого переменного (теорема подобия)



где а — постоянный вещественный коэффициент. Свойство (9) легко доказывается путем замены независимой переменной t = atв прямом преобразовании Лапласа (2).

Смещение в области действительного переменного (теорема запаздывания)



Для доказательства (7.10) введем следующие обозначения:



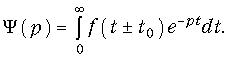
Осуществим замену переменной t = t ± t₀.



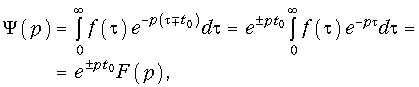
что и требовалось доказать.

Из соотношения (10) следует, что сдвиг оригинала по оси времени на t₀ соответствует умножению изображения на   .

Смещения в области комплексного переменного (теорема смещения)



Теорема (11) следует непосредственно из прямого преобразования Лапласа, если в (2) вместо f(t) подставить 

---

 . Причем l может быть как действительной, так и комплексной величиной.

Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности)





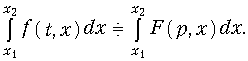
Для доказательства свойств (12), (13) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (2) по параметру х.

Произведение изображений



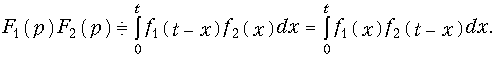
Интегралы в (14) носят название свертки функций f₁(t) и f₂(t).

Дифференцирование изображения



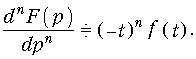
Свойство (15) легко доказывается путем дифференцирования прямого преобразования Лапласа (2).

Интегрирование изображения



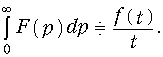
Данное свойство доказывается аналогично (15).

В заключение приведем предельные соотношения для оригинала и изображения:





Действительно, согласно свойства дифференцирования оригинала можно записать:



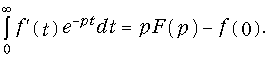
Учитывая, что   , получаем:



Отсюда непосредственно следует соотношение (17). Аналогично доказывается равенство (18).



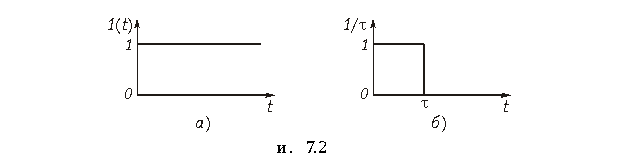
Рис.2.

В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции d(t) (функция Дирака).

---

Единичная функция задается уравнением (рис.2, а)



Изображение функции (7.19) будет равно:



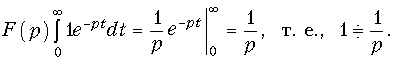
Единичная импульсная функция (функция Дирака). Эта функция называется еще d-функцией; она задается уравнением



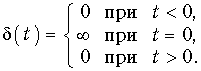
Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при t ® 0) единичного импульса (см. рис. 7.2, б), площадь которого равна единице:



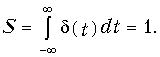
В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций.

2. Непрерывное преобразование Лапласа

Одним из способов решения дифференциальных уравнений (систем уравнений) с постоянными коэффициентами является метод интегральных преобразований, который позволяет функцию вещественной переменной (оригинал функции) заменить функцией комплексной переменной (изображение функции). В результате операции дифференцирования и интегрирования в пространстве функций-оригиналов преобразуются в алгебраическое умножение и деление в пространстве функций-изображений. Одним из представителей метода интегральных преобразований является Преобразование Лапласа.

Непрерывное преобразование Лапласа  – интегральное преобразование, связывающее функцию комплексной переменной   (изображение функции) с функцией вещественной переменной    (оригинал функции). При этом функция вещественной переменной   должна удовлетворять следующим условиям:

- функция определена и дифференцируема на всей положительной полуоси вещественной переменной 

---