Файл: Целью работы является анализ преобразований Лапласа.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 81
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
то по формуле (5) получим:
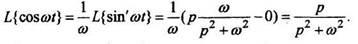
3. Дифференцирование изображения.Если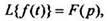
то 
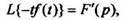т.е. дифференцирование изображения сводится к умножению на 
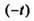оригинала. В общем случае,
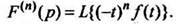(9)
Пример 5. Определить изображения функций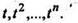
РЕШЕНИЕ
Так как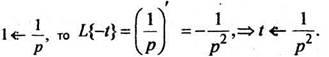
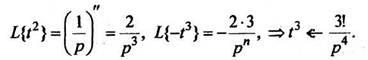
В общем случае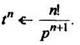
4. Интегрирование оригинала.Интегрирование оригинала сводится к делению изображения на р:
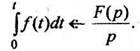(10)
Пример 6. Найти изображение функци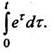
РЕШЕНИЕ Так как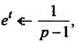
то по формуле (10)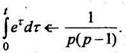 
5. Интегрирование изображения.Интефирование изображения равносильно делению на tоригинала (если существует конечный предел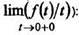
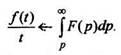(11)
Пример 7. Найдем изображение функции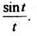
Так как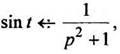
то по формуле (11) получаем
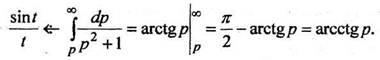
6. Теорема смещенияПри умножении оригинала на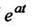
изображение получается смещение аргумента на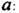 
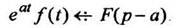(12)
+Пример 8. В примерах 3, 4, 5 найдены изображения функций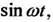
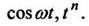По формуле (12) находим: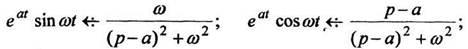 
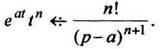
Нахождение изображений функции времени (равно как и обратные переходы от изображений к оригиналу) выполняются с помощью специальных интегральных преобразований, приводимых в курсе высшей математики. В настоящее время в большей части современной технической литературы операторные методы связывают с применением преобразования Лапласа.
Важно отметить, что функции, описывающие реально возможные воздействия и соответствующие им реакции, всегда преобразуемы по Лапласу.
1. Информационные технологии и вычислительные системы. Вычислительные системы. Компьютерная графика. Распознавание образов. Математическое моделирование / Под ред. С.В. Емельянова. - М.: Ленанд, 2015. - 100 c.
2. Информационные технологии и вычислительные системы: Обработка информации и анализ данных. Программная инженерия. Математическое моделирование. Прикладные аспекты информатики / Под ред. С.В. Емельянова. - М.: Ленанд, 2015. - 104 c.
3. Акаев, А.А. От эпохи великой дивергенции к эпохе великой конвергенции: Математическое моделирование и прогнозирование долгосроч. технологич. и экономич. развития / А.А. Акаев. - М.: Ленанд, 2015. - 352 c.
4. Акаев, А.А. От эпохи Великой дивергенции к эпохе Великой конвергенции: Математическое моделирование и прогнозирование долгосрочного технологического и экономического развития мировой динамики / А.А. Акаев. - М.: Ленанд, 2019. - 352 c.
5. Александров, А., Ю. Математическое моделирование и исследование устойчивости биологических сообществ: Учебное пособие / А.Ю. Александров, А. Платонов. - СПб.: Лань, 2016. - 272 c.
6. Александров, А.Ю. Математическое моделирование и исследование устойчивости биологических сообществ: Учебное пособие / А.Ю. Александров, А.В. Платонов и др. - СПб.: Лань, 2017. - 320 c.
7. Алпатов, Ю.Н. Математическое моделирование производственных процессов: Учебное пособие / Ю.Н. Алпатов. - СПб.: Лань, 2018. - 136 c.
8. Белотелов, Н.В. Сложность. Математическое моделирование. Гуманитарный анализ: Исследование исторических, военных, социально-экономических и политических процессов / Н.В. Белотелов, Ю.И. Бродский, Ю.Н. Павловский. - М.: КД Либроком, 2019. - 320 c.
9. Бобренева, И.В. Математическое моделирование в технологиях продуктов питания животного происхождения: Учебное пособие / И.В. Бобренева, С.В. Николаева. - СПб.: Лань, 2019. - 124 c.
10. Виноградов, Ю.Б. Математическое моделирование в гидрологии / Ю.Б. Виноградов. - М.: Academia, 2017. - 272 c.
11. Волгина, О.А. Математическое моделирование экономических процессов и систем: Учебное пособие / О.А. Волгина, Н.Ю. Голодная, Н.Н. Одияко. - М.: КноРус, 2016. - 395 c.
12. Голубева, Н.В. Математическое моделирование систем и процессов. Учебное пособие / Н.В. Голубева. - СПб.: Лань, 2016. - 192 c.
13. Горбунов, В.К. Математическое моделирование рыночного спроса: Учебное пособие / В.К. Горбунов. - СПб.: Лань, 2018. - 212 c.
14. Горлач, Б.А. Математическое моделирование. Построение моделей и численная реализация / Б.А. Горлач, В.Г. Шахов. - СПб.: Лань, 2016. - 292 c.
15. Горлач, Б.А. Математическое моделирование. Построение моделей и численная реализация: Учебное пособие / Б.А. Горлач, В.Г. Шахов. - СПб.: Лань, 2018. - 292 c.
16. Данилов, Н.Н. Математическое моделирование радиотехнических систем: Учебное пособие / Н.Н. Данилов. - СПб.: Лань, 2016. - 144 c.
17. Димитрин, Ю. Математическое моделирование и исследование устойчивости биологических сообществ: Учебное пособие / Ю. Димитрин. - СПб.: Лань, 2016. - 272 c.
18. Жирков, А.М. Математическое моделирование систем и процессов: Учебное пособие / А.М. Жирков, Г.М. Подопригора, М.Р. Цуцунава. - СПб.: Лань КПТ, 2016. - 192 c.
19. Зайдель, А.Н. Математическое моделирование. Построение моделей и численная реализация: Учебное пособие / А.Н. Зайдель. - СПб.: Лань, 2016. - 304 c.
20. Зубарев, Ю.М. Математическое моделирование многоагентных систем конкуренции и кооперации (Теория игр для всех): Учебное пособие / Ю.М. Зубарев, С.В. Косаревский. - СПб.: Лань П, 2016. - 624 c.
21. Иванов, В.К. Математическое моделирование и оптимизация лучевой терапии опухолей / В.К. Иванов. - М.: Ленанд, 2015. - 152 c.
3. Дифференцирование изображения.Если
то т.е. дифференцирование изображения сводится к умножению на оригинала. В общем случае, (9)Пример 5. Определить изображения функций
РЕШЕНИЕ
Так как
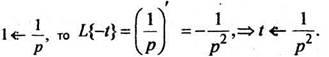
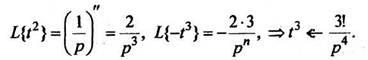
В общем случае
4. Интегрирование оригинала.Интегрирование оригинала сводится к делению изображения на р:
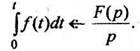(10)Пример 6. Найти изображение функци
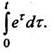
РЕШЕНИЕ Так как
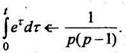
то по формуле (10) 5. Интегрирование изображения.Интефирование изображения равносильно делению на tоригинала (если существует конечный предел
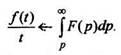(11)Пример 7. Найдем изображение функции
Так как
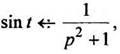то по формуле (11) получаем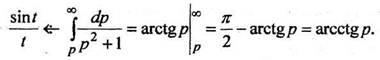
6. Теорема смещенияПри умножении оригинала на
изображение получается смещение аргумента на (12)+Пример 8. В примерах 3, 4, 5 найдены изображения функций
По формуле (12) находим: Заключение
Нахождение изображений функции времени (равно как и обратные переходы от изображений к оригиналу) выполняются с помощью специальных интегральных преобразований, приводимых в курсе высшей математики. В настоящее время в большей части современной технической литературы операторные методы связывают с применением преобразования Лапласа.
Важно отметить, что функции, описывающие реально возможные воздействия и соответствующие им реакции, всегда преобразуемы по Лапласу.
Список литературы
1. Информационные технологии и вычислительные системы. Вычислительные системы. Компьютерная графика. Распознавание образов. Математическое моделирование / Под ред. С.В. Емельянова. - М.: Ленанд, 2015. - 100 c.
2. Информационные технологии и вычислительные системы: Обработка информации и анализ данных. Программная инженерия. Математическое моделирование. Прикладные аспекты информатики / Под ред. С.В. Емельянова. - М.: Ленанд, 2015. - 104 c.
3. Акаев, А.А. От эпохи великой дивергенции к эпохе великой конвергенции: Математическое моделирование и прогнозирование долгосроч. технологич. и экономич. развития / А.А. Акаев. - М.: Ленанд, 2015. - 352 c.
4. Акаев, А.А. От эпохи Великой дивергенции к эпохе Великой конвергенции: Математическое моделирование и прогнозирование долгосрочного технологического и экономического развития мировой динамики / А.А. Акаев. - М.: Ленанд, 2019. - 352 c.
5. Александров, А., Ю. Математическое моделирование и исследование устойчивости биологических сообществ: Учебное пособие / А.Ю. Александров, А. Платонов. - СПб.: Лань, 2016. - 272 c.
6. Александров, А.Ю. Математическое моделирование и исследование устойчивости биологических сообществ: Учебное пособие / А.Ю. Александров, А.В. Платонов и др. - СПб.: Лань, 2017. - 320 c.
7. Алпатов, Ю.Н. Математическое моделирование производственных процессов: Учебное пособие / Ю.Н. Алпатов. - СПб.: Лань, 2018. - 136 c.
8. Белотелов, Н.В. Сложность. Математическое моделирование. Гуманитарный анализ: Исследование исторических, военных, социально-экономических и политических процессов / Н.В. Белотелов, Ю.И. Бродский, Ю.Н. Павловский. - М.: КД Либроком, 2019. - 320 c.
9. Бобренева, И.В. Математическое моделирование в технологиях продуктов питания животного происхождения: Учебное пособие / И.В. Бобренева, С.В. Николаева. - СПб.: Лань, 2019. - 124 c.
10. Виноградов, Ю.Б. Математическое моделирование в гидрологии / Ю.Б. Виноградов. - М.: Academia, 2017. - 272 c.
11. Волгина, О.А. Математическое моделирование экономических процессов и систем: Учебное пособие / О.А. Волгина, Н.Ю. Голодная, Н.Н. Одияко. - М.: КноРус, 2016. - 395 c.
12. Голубева, Н.В. Математическое моделирование систем и процессов. Учебное пособие / Н.В. Голубева. - СПб.: Лань, 2016. - 192 c.
13. Горбунов, В.К. Математическое моделирование рыночного спроса: Учебное пособие / В.К. Горбунов. - СПб.: Лань, 2018. - 212 c.
14. Горлач, Б.А. Математическое моделирование. Построение моделей и численная реализация / Б.А. Горлач, В.Г. Шахов. - СПб.: Лань, 2016. - 292 c.
15. Горлач, Б.А. Математическое моделирование. Построение моделей и численная реализация: Учебное пособие / Б.А. Горлач, В.Г. Шахов. - СПб.: Лань, 2018. - 292 c.
16. Данилов, Н.Н. Математическое моделирование радиотехнических систем: Учебное пособие / Н.Н. Данилов. - СПб.: Лань, 2016. - 144 c.
17. Димитрин, Ю. Математическое моделирование и исследование устойчивости биологических сообществ: Учебное пособие / Ю. Димитрин. - СПб.: Лань, 2016. - 272 c.
18. Жирков, А.М. Математическое моделирование систем и процессов: Учебное пособие / А.М. Жирков, Г.М. Подопригора, М.Р. Цуцунава. - СПб.: Лань КПТ, 2016. - 192 c.
19. Зайдель, А.Н. Математическое моделирование. Построение моделей и численная реализация: Учебное пособие / А.Н. Зайдель. - СПб.: Лань, 2016. - 304 c.
20. Зубарев, Ю.М. Математическое моделирование многоагентных систем конкуренции и кооперации (Теория игр для всех): Учебное пособие / Ю.М. Зубарев, С.В. Косаревский. - СПб.: Лань П, 2016. - 624 c.
21. Иванов, В.К. Математическое моделирование и оптимизация лучевой терапии опухолей / В.К. Иванов. - М.: Ленанд, 2015. - 152 c.