Файл: Целью работы является анализ преобразований Лапласа.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 80
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
в знаменателе, функция раскладывается на дробь типа: 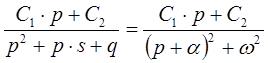
∙ В общем случае если изображение функции представляет собой правильную рациональную дробь (степень числителя меньше степени знаменателя рациональной дроби), то ее можно разложить на сумму простейших дробей.
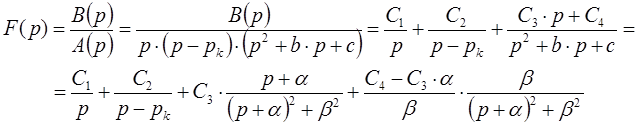
Далее для каждой простейшей дроби определяется оригинал функции в соответствии с типовыми таблицами.
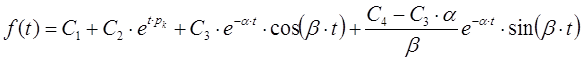
∙ В частном случае если знаменатель изображения функции раскладывается только на простые корни уравнения, то изображение функции можно разложить на сумму простейших дробей следующим образом:
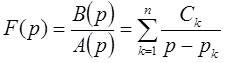
Неизвестные коэффициенты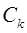 могут быть определены методом неопределённых коэффициентов или упрощенным способом по следующей формуле:
могут быть определены методом неопределённых коэффициентов или упрощенным способом по следующей формуле:
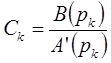
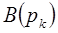 - значение функции в точке
- значение функции в точке 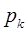 ;
;
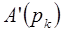 - значение производной функции в точке
- значение производной функции в точке 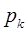 .
.
Оригинал данной функции будет определяться следующим образом:
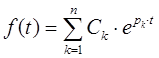
В качестве примера определим оригинал функции, при условии, что его изображение определяется следующим образом:
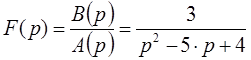
Раскладываем знаменатель на множители и перепишем изображение функции с учетом введение в уравнение неизвестных коэффициентов:
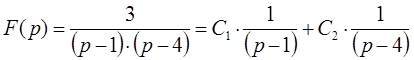
Неизвестные коэффициенты в выражении будут определяться по формуле следующим образом:
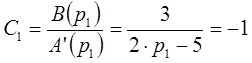
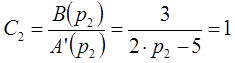
Таким образом, изображение функции имеет следующий вид:
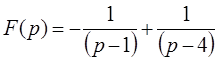
В результате определяем оригинал функции:
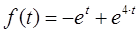
Следует отметить, что в случае если знаменатель имеет нулевой корень, то упрощенная формула для определения неопределённых коэффициентов имеет другой вид:
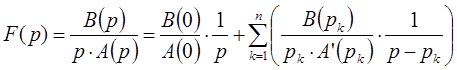
В качестве примера определим оригинал функции, при условии, что его изображение определяется следующим образом:
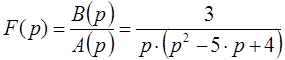
Раскладываем знаменатель на множители и перепишем изображение функции с учетом введение в уравнение неизвестных коэффициентов:
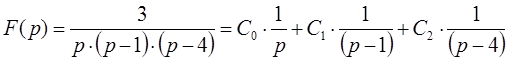
Неизвестные коэффициенты в выражении будут определяться по формуле следующим образом:
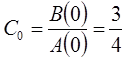
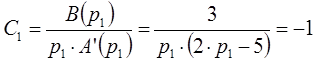
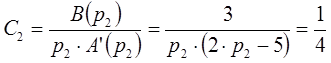
Таким образом, изображение функции имеет следующий вид:
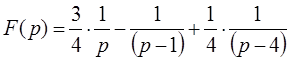
В результате оригинал функции будет определяться следующим выражением:
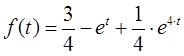
Преобразования Лапласа применяются в математике, физике, оптике, электротехнике, технике автоматического управления, обработке сигналов и теории вероятности. Данное преобразование было предложено Пьером-Симоном де Лапласом в XVIII веке в процессе работы над теорией вероятности. В настоящее время преобразование Лапласа используется при решении систем дифференциальных и интегральных уравнений, а также при расчете/анализе передаточных функций линейных динамических систем, таких как электрические схемы, гармонические осцилляторы, оптические приборы и механические системы.
Функцией- оригиналом - называют функцию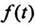 действительного аргумента
действительного аргумента
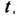 удовлетворяющую условиям:
удовлетворяющую условиям:
1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е.
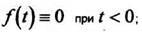
2) функция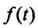 при
при 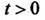 возрастает не быстрее показательной функции, т.е. существ.уют такие постоянные
возрастает не быстрее показательной функции, т.е. существ.уют такие постоянные 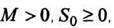 что
что
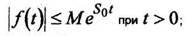
3) на любом конечном отрезке положительной полуоси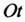 функция
функция 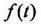 и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода.
и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода.
Простейшей функцией - оригиналом является единичная функция Хевисайда
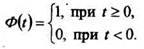 (1)
(1)
Если функция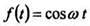 не удовлетворяет условию
не удовлетворяет условию 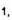 то произведение
то произведение 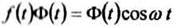 уже ему удовлетворяет, т.е. будет оригиналом.
уже ему удовлетворяет, т.е. будет оригиналом.
Для простоты записи множитель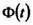 опускается, например, пишут
опускается, например, пишут 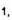 вместо
вместо 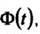
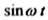
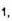 вместо
вместо 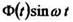 и т.д.
и т.д.
Изображением функции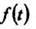 по Лапласу (преобразованием по Лапласу) называют функцию комплексной переменной
по Лапласу (преобразованием по Лапласу) называют функцию комплексной переменной 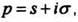 определяемую соотношением
определяемую соотношением
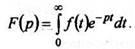 (2)
(2)
Интеграл (1.2) называют интегралом Лапласа.
Функция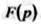 определяется в полуплоскости
определяется в полуплоскости 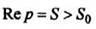 и является в этой области аналитической функцией.
и является в этой области аналитической функцией.
То, что функция комплексной переменной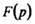 является изображением по Лапласу функции действительного аргумента
является изображением по Лапласу функции действительного аргумента 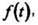 обозначается
обозначается 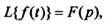 или
или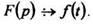
Изображение элементарных функций получается непосредственно с помощью интеграла (2).
Пример 1 Найти изображение по Лапласу функции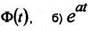
РЕШЕНИЕ
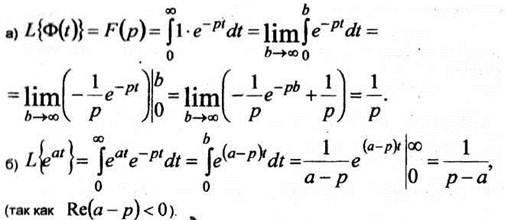
Таким образом, получаем
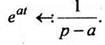
Преобразование, основанное на интеграле Лапласа (2), обладает линейными свойсгыами.
1. Преобразование суммы функций равно сумме преобразований этих функций
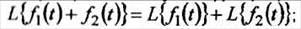
2 Постоянный множитель можно выносить за знак преобразования:
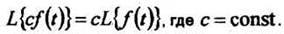
Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований:
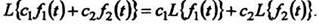 (3)
(3)
Пример 2. Найти изображение функции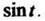
РЕШЕНИЕ
Используем формулу (2) для функции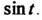 Тогда
Тогда
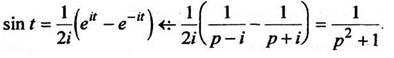
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
1. Теорема подобияЕсли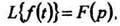 то для любого постоянногоа > 0
то для любого постоянногоа > 0
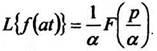 (4)
(4)
Пример 3. Найдем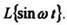 Из примера2
Из примера2 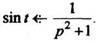 .По Формуле (4)
.По Формуле (4)
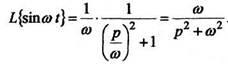
2.Дифференцирование оригиналаЕсли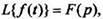 то
то
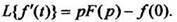 (5)
(5)
Методом индукции на основании формулы (5) получены формулы изображения высших производных:
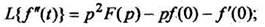 (6)
(6)
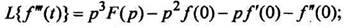 (7)
(7)
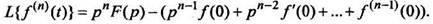 (8)
(8)
Пример 4. Определим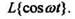 Так как
Так как 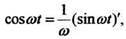
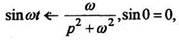
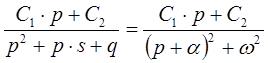
∙ В общем случае если изображение функции представляет собой правильную рациональную дробь (степень числителя меньше степени знаменателя рациональной дроби), то ее можно разложить на сумму простейших дробей.
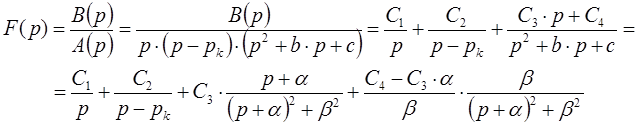
Далее для каждой простейшей дроби определяется оригинал функции в соответствии с типовыми таблицами.
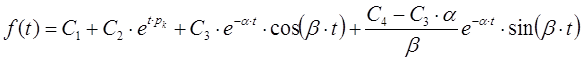
∙ В частном случае если знаменатель изображения функции раскладывается только на простые корни уравнения, то изображение функции можно разложить на сумму простейших дробей следующим образом:
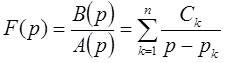
Неизвестные коэффициенты
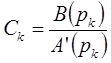
Оригинал данной функции будет определяться следующим образом:
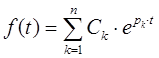
В качестве примера определим оригинал функции, при условии, что его изображение определяется следующим образом:
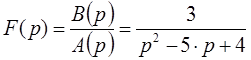
Раскладываем знаменатель на множители и перепишем изображение функции с учетом введение в уравнение неизвестных коэффициентов:
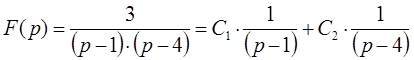
Неизвестные коэффициенты в выражении будут определяться по формуле следующим образом:
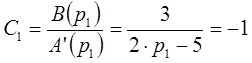
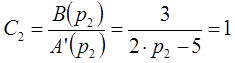
Таким образом, изображение функции имеет следующий вид:
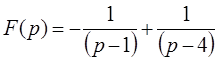
В результате определяем оригинал функции:
Следует отметить, что в случае если знаменатель имеет нулевой корень, то упрощенная формула для определения неопределённых коэффициентов имеет другой вид:
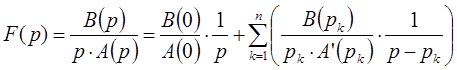
В качестве примера определим оригинал функции, при условии, что его изображение определяется следующим образом:
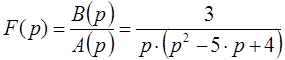
Раскладываем знаменатель на множители и перепишем изображение функции с учетом введение в уравнение неизвестных коэффициентов:
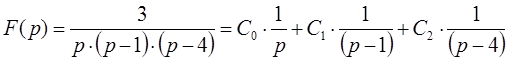
Неизвестные коэффициенты в выражении будут определяться по формуле следующим образом:
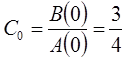
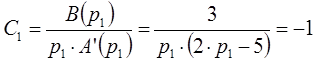
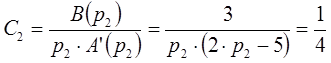
Таким образом, изображение функции имеет следующий вид:
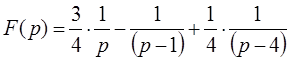
В результате оригинал функции будет определяться следующим выражением:
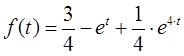
Преобразования Лапласа применяются в математике, физике, оптике, электротехнике, технике автоматического управления, обработке сигналов и теории вероятности. Данное преобразование было предложено Пьером-Симоном де Лапласом в XVIII веке в процессе работы над теорией вероятности. В настоящее время преобразование Лапласа используется при решении систем дифференциальных и интегральных уравнений, а также при расчете/анализе передаточных функций линейных динамических систем, таких как электрические схемы, гармонические осцилляторы, оптические приборы и механические системы.
-
Применение преобразования Лапласа
Функцией- оригиналом - называют функцию
1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е.
2) функция
3) на любом конечном отрезке положительной полуоси
Простейшей функцией - оригиналом является единичная функция Хевисайда
Если функция
Для простоты записи множитель
Изображением функции
Интеграл (1.2) называют интегралом Лапласа.
Функция
То, что функция комплексной переменной
Изображение элементарных функций получается непосредственно с помощью интеграла (2).
Пример 1 Найти изображение по Лапласу функции
РЕШЕНИЕ
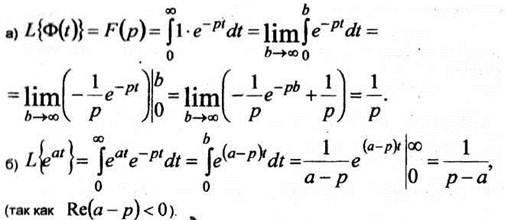
Таким образом, получаем
Преобразование, основанное на интеграле Лапласа (2), обладает линейными свойсгыами.
1. Преобразование суммы функций равно сумме преобразований этих функций
2 Постоянный множитель можно выносить за знак преобразования:
Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований:
Пример 2. Найти изображение функции
РЕШЕНИЕ
Используем формулу (2) для функции
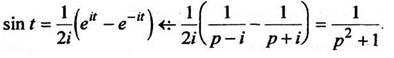
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
1. Теорема подобияЕсли
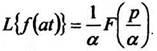 (4)
(4)Пример 3. Найдем
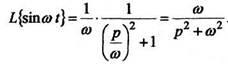
2.Дифференцирование оригиналаЕсли
Методом индукции на основании формулы (5) получены формулы изображения высших производных:
Пример 4. Определим