Файл: Кластер с014 п графические задачи, кластеры Кинематика вращательного движения твердого тела. П ( 15 шт).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 593
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Сингл S014 П Кинематика вращательного движения твердого тела. Аналитические задачи, П (s014, 15 шт)
v211 –П Электрическое поле, закон Кулона, напряженность электрического поля
v214 П Электрическое поле. Потенциал, работа, связь напряженности и разности потенциалов
v217.Электроемкость П. Конденсаторы, Энергия ЭП
31 П Магнитное поле. Графическое изображение полей. Индукция МП
f(v) зависит от массы молекулы газа
2) функция распределения Максвелла f(v) не зависит от температуры
3) f(v) является величиной размерной
4) f(v) носит экстремальный характер
:1,3,4
3. При изменении температуры Т газа средняя квадратичная скорость молекул этого газа увеличилась в 3 раза. Тогда максимальное значение функции распределения Максвелла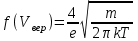 (e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а).
(e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а).
1) увеличится в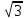
2) уменьшится в 9
3) уменьшится в 3
4) увеличится в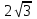
: 3
4. Правильные утверждения о средней квадратичной скорости (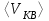 ) частиц системы, подчиняющейся распределению Максвелла:
) частиц системы, подчиняющейся распределению Максвелла:
1) При одинаковой температуре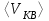 молекул различных идеальных газов одинакова.
молекул различных идеальных газов одинакова.
2) Средняя квадратичная скорость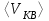 молекул газа при любой температуре меньше наиболее вероятной скорости.
молекул газа при любой температуре меньше наиболее вероятной скорости.
3) Чем больше масса молекулы газа, тем меньше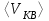 .
.
4) При возрастании температуры системы в четыре раза средняя квадратичная скорость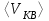 молекул увеличивается в два раза.
молекул увеличивается в два раза.
:3,4
5. Если средняя квадратичная скорость молекул водорода (M = 210-3 кг/моль) больше наиболее вероятной на V= 400 м/с, то температура газа равна … К.
1) 180
2) 381
3) 230
4) 450
:2
6. Если средняя квадратичная скорость молекул некоторого газа равна 500 м/с, то наиболее вероятная скорость составляет … м/с.
1) 327
2) 250
3) 630
4) 408
:4
7. Если при нагревании некоторого газа наиболее вероятная скорость молекул газа увеличилась в 2 раза, то средняя квадратичная скорость … раз(а).
1) увеличится в 4
2) уменьшится в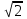
3) уменьшится в 8
4) увеличится в 2
:4
8. Если при нагревании некоторого газа средняя квадратичная скорость молекул газа увеличилась в 4 раза, при этом наиболее вероятная скорость … раз(а).
1) увеличится в 4
2) уменьшится в
3) уменьшится в 8
4) увеличится в 2
:1
9. Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда значение f(Vвер) функции распределения Максвелла, соответствующее наиболее вероятной скорости молекул,..
1)одинаково для всех газов
2) максимально для водорода
3) минимально для гелия
4) максимально для кислорода
:4
10. Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда наиболее вероятная скорость Vвер…
1) у всех газов одинакова
2) у кислорода наибольшая
3) у гелия наименьшая
4) у водорода наибольшая
: 4
11В статистике Максвелла функция распределения имеет вид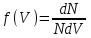 . НЕВЕРНОЕ утверждение о функции Максвелла –
. НЕВЕРНОЕ утверждение о функции Максвелла –
1) f(V) - вероятность того, что скорость данной молекулы находится в единичном интервале скоростей вблизи заданной скорости V.
2) f(V)dV- вероятность того, что скорость данной молекулы заключена в интервале скоростей от V до V+dV.
3) f(V) - относительное число молекул, скорости которых заключены в интервале скоростей от V до V+dV.
4) f(V)NdV - абсолютное число молекул, скорости которых заключены в интервале скоростей от V до V+dV.
:4
12Правильные утверждения о наиболее вероятной скорости Vвер частиц системы, подчиняющейся распределению Максвелла:
1) Наиболее вероятная скорость Vвер зависит от температуры и молярной массы идеального газа.
2) Скорость Vвер можно найти, приравняв нулю производную функции распределения Максвелла по скоростям: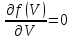 .
.
3) Чем больше молярная масса газа, тем меньше при данной температуре значение Vвер.
4) Vвер линейно возрастает с увеличением температуры.
:1,2,3
13. . Н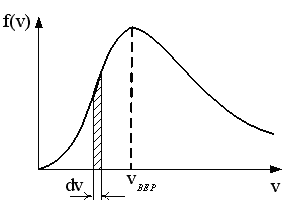 а рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где
а рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 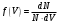
- доля молекул, скорости которых заключены в интервале от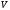 до
до 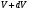 в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то
в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то
1) величина максимума уменьшится
2) площадь под кривой увеличится
3) максимум кривой сместится влево, в сторону меньших скоростей
4) максимум кривой сместится вправо, в сторону больших скоростей
:3
ема: 121 Первое начало термодинамики
V121П Первое начало термодинамики.
S121 П Первое начало термодинамики (23 задания)
1. Для адиабатического процесса в идеальном газе справедливы утверждения:
1) В ходе процесса газ не обменивается энергией с окружающими его телами (ни в форме работы, ни в форме теплопередачи).
2) Если газ расширяется, то его внутренняя энергия уменьшается.
3) Если газ расширяется, то его внутренняя энергия увеличивается.
4) В ходе процесса изменяются параметры состояния газа – объем, давление, температура.
: 2, 4
2 Правильные утверждения о внутренней энергии системы:
1) внутренняя энергия системы является функцией ее состояния – зависит от ее термодинамических параметров состояния
2) во внутреннюю энергию системы не входит механическая энергия движения и взаимодействия системы как целого
3) приращение внутренней энергии зависит от пути (способа) перехода системы из начального состояния в конечное
4) внутренние энергии двух тел, находящихся в тепловом равновесии друг с другом, всегда одинаковы
: 1, 2
3. ). Двухатомному идеальному газу в результате изобарического процесса подведено количество теплоты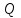 . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты 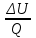 , равная
, равная
1) 0,29
2) 0,71
3) 0,60
4) 0,25
:2
4. [Уд] (ВО1) Формулировками первого начала термодинамики могут служить утверждения:
1) В адиабатически замкнутой системе энтропия при любых процессах не может убывать.
2) Количество тепла, подведенное к системе, затрачивается на изменение ее внутренней энергии и на совершение системой работы против внешних сил.
3) При любом круговом процессе система может совершить работу
, большую, чем подведенное к ней количество теплоты.
4)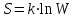 , где S– энтропия системы, k–постоянная Больцмана, аW– термодинамическая вероятность.
, где S– энтропия системы, k–постоянная Больцмана, аW– термодинамическая вероятность.
: 2
5. [Уд1] (ВО1) В результате изобарического нагревания одного моля идеального двухатомного газа, имеющего начальную температуру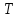 , его объем увеличился в 2 раза. Для этого к газу надо подвести количество теплоты, равное
, его объем увеличился в 2 раза. Для этого к газу надо подвести количество теплоты, равное
1)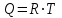
2)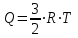
3)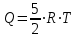
4)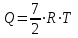
:4
6. [Уд1] (ВО1) Двум молям водорода сообщили 580 Дж теплоты при постоянном давлении. При этом его температура повысилась на … К.
1) 10
2) 27
3) 38
4) 45
:1
7. [Уд1] (ВО1) У водорода, взятом в количестве 2 моль при постоянном давлении, температура повысилась на 10 К. При этом ему сообщили количество теплоты, равное … Дж.
1) 370
2) 580
3) 640
4) 925
:2
8. [Уд1] (ВО1) Водороду, имеющему постоянный объем, сообщили 580 Дж теплоты и его температура повысилась на 10 К. Количество вещества составляет … моль.
1) 2,8
2) 3,5
3) 4,7
4) 6,8
:1
9. [Уд] (ВО1). Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты . На работу газа расходуется часть теплоты
. На работу газа расходуется часть теплоты 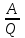 , равная
, равная
1) 0,40
2) 0,75
3) 0,60
4) 0,25
:1
10. [Уд] (ВО1). Двухатомному идеальному газу в результате изобарического процесса подведено количество теплоты . На работу газа расходуется часть теплоты
. На работу газа расходуется часть теплоты 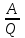 , равная
, равная
1) 0,41
2) 0,73
3) 0,56
4) 0,29
:4
11. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изобарического и кругового процессов в идеальных газах, приведены под номерами:
1) Q= U+ A
2) 0 = U + A
3) Q = U
4) Q = A
:1, 4
12. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изохорического и изотермического процессов в идеальных газах, приведены под номерами:
1) Q= U+ A
2) 0 = U + A
3) Q = U
4) Q = A
:3, 4
13. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изохорического и изобарического процессов в идеальных газах, приведены под номерами:
1) Q= U+ A
2) 0 = U + A
3) Q = U
4) Q = A
:1, 3
14. [Уд1] (ВО1) Работа, совершаемая в изотермическом процессе, определяется формулой
1)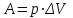
2)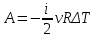
3)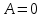
4)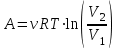
:4
15. [Уд1] (ВО1) Работа, совершаемая газом в изохорическом процессе, определяется формулой под номером
1)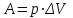
2)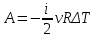
3)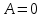
4)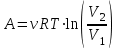
:3
16. [Уд1] (ВО) Внутренняя энергия идеального двухатомного газа выражается формулой
1)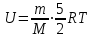
2)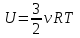
3)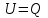
4)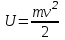
: 1
17. [Уд] (ВО1). Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты  , равная
, равная
1) 0,40
2) 0,75
3) 0,60
4) 0,25
:3
18. [Уд1] (ВО1) При изобарическом процессе в идеальном газе его объем возрос в два раза. Внутренняя энергия газа при этом
1) увеличилась в два раза
2) уменьшилась в два раза
3) не изменилась
4) увеличилась в 4 раза
:1
19. [Уд1] (ВО1) Один моль одноатомного идеального газа, имеющий начальную температуру T = 250 К, нагрели изобарически. При этом его объем увеличился в 2 раза. Изменение внутренней энергии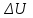 газа равно … кДж.
газа равно … кДж.
1) 2,7
2) 3,1
3) 3,8
4) 4,5
: 2
2) функция распределения Максвелла f(v) не зависит от температуры
3) f(v) является величиной размерной
4) f(v) носит экстремальный характер
:1,3,4
3. При изменении температуры Т газа средняя квадратичная скорость молекул этого газа увеличилась в 3 раза. Тогда максимальное значение функции распределения Максвелла
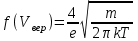 (e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а).
(e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а).1) увеличится в
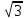
2) уменьшится в 9
3) уменьшится в 3
4) увеличится в
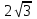
: 3
4. Правильные утверждения о средней квадратичной скорости (
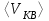 ) частиц системы, подчиняющейся распределению Максвелла:
) частиц системы, подчиняющейся распределению Максвелла:1) При одинаковой температуре
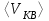 молекул различных идеальных газов одинакова.
молекул различных идеальных газов одинакова.2) Средняя квадратичная скорость
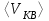 молекул газа при любой температуре меньше наиболее вероятной скорости.
молекул газа при любой температуре меньше наиболее вероятной скорости.3) Чем больше масса молекулы газа, тем меньше
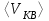 .
.4) При возрастании температуры системы в четыре раза средняя квадратичная скорость
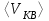 молекул увеличивается в два раза.
молекул увеличивается в два раза.:3,4
5. Если средняя квадратичная скорость молекул водорода (M = 210-3 кг/моль) больше наиболее вероятной на V= 400 м/с, то температура газа равна … К.
1) 180
2) 381
3) 230
4) 450
:2
6. Если средняя квадратичная скорость молекул некоторого газа равна 500 м/с, то наиболее вероятная скорость составляет … м/с.
1) 327
2) 250
3) 630
4) 408
:4
7. Если при нагревании некоторого газа наиболее вероятная скорость молекул газа увеличилась в 2 раза, то средняя квадратичная скорость … раз(а).
1) увеличится в 4
2) уменьшится в
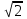
3) уменьшится в 8
4) увеличится в 2
:4
8. Если при нагревании некоторого газа средняя квадратичная скорость молекул газа увеличилась в 4 раза, при этом наиболее вероятная скорость … раз(а).
1) увеличится в 4
2) уменьшится в

3) уменьшится в 8
4) увеличится в 2
:1
9. Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда значение f(Vвер) функции распределения Максвелла, соответствующее наиболее вероятной скорости молекул,..
1)одинаково для всех газов
2) максимально для водорода
3) минимально для гелия
4) максимально для кислорода
:4
10. Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда наиболее вероятная скорость Vвер…
1) у всех газов одинакова
2) у кислорода наибольшая
3) у гелия наименьшая
4) у водорода наибольшая
: 4
11В статистике Максвелла функция распределения имеет вид
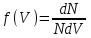 . НЕВЕРНОЕ утверждение о функции Максвелла –
. НЕВЕРНОЕ утверждение о функции Максвелла – 1) f(V) - вероятность того, что скорость данной молекулы находится в единичном интервале скоростей вблизи заданной скорости V.
2) f(V)dV- вероятность того, что скорость данной молекулы заключена в интервале скоростей от V до V+dV.
3) f(V) - относительное число молекул, скорости которых заключены в интервале скоростей от V до V+dV.
4) f(V)NdV - абсолютное число молекул, скорости которых заключены в интервале скоростей от V до V+dV.
:4
12Правильные утверждения о наиболее вероятной скорости Vвер частиц системы, подчиняющейся распределению Максвелла:
1) Наиболее вероятная скорость Vвер зависит от температуры и молярной массы идеального газа.
2) Скорость Vвер можно найти, приравняв нулю производную функции распределения Максвелла по скоростям:
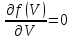 .
.3) Чем больше молярная масса газа, тем меньше при данной температуре значение Vвер.
4) Vвер линейно возрастает с увеличением температуры.
:1,2,3
13. . Н
 а рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где
а рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 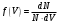
- доля молекул, скорости которых заключены в интервале от
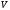 до
до 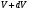 в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то
в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то1) величина максимума уменьшится
2) площадь под кривой увеличится
3) максимум кривой сместится влево, в сторону меньших скоростей
4) максимум кривой сместится вправо, в сторону больших скоростей
:3
ема: 121 Первое начало термодинамики
V121П Первое начало термодинамики.
S121 П Первое начало термодинамики (23 задания)
1. Для адиабатического процесса в идеальном газе справедливы утверждения:
1) В ходе процесса газ не обменивается энергией с окружающими его телами (ни в форме работы, ни в форме теплопередачи).
2) Если газ расширяется, то его внутренняя энергия уменьшается.
3) Если газ расширяется, то его внутренняя энергия увеличивается.
4) В ходе процесса изменяются параметры состояния газа – объем, давление, температура.
: 2, 4
2 Правильные утверждения о внутренней энергии системы:
1) внутренняя энергия системы является функцией ее состояния – зависит от ее термодинамических параметров состояния
2) во внутреннюю энергию системы не входит механическая энергия движения и взаимодействия системы как целого
3) приращение внутренней энергии зависит от пути (способа) перехода системы из начального состояния в конечное
4) внутренние энергии двух тел, находящихся в тепловом равновесии друг с другом, всегда одинаковы
: 1, 2
3. ). Двухатомному идеальному газу в результате изобарического процесса подведено количество теплоты
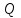 . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты 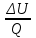 , равная
, равная 1) 0,29
2) 0,71
3) 0,60
4) 0,25
:2
4. [Уд] (ВО1) Формулировками первого начала термодинамики могут служить утверждения:
1) В адиабатически замкнутой системе энтропия при любых процессах не может убывать.
2) Количество тепла, подведенное к системе, затрачивается на изменение ее внутренней энергии и на совершение системой работы против внешних сил.
3) При любом круговом процессе система может совершить работу
, большую, чем подведенное к ней количество теплоты.
4)
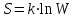 , где S– энтропия системы, k–постоянная Больцмана, аW– термодинамическая вероятность.
, где S– энтропия системы, k–постоянная Больцмана, аW– термодинамическая вероятность.: 2
5. [Уд1] (ВО1) В результате изобарического нагревания одного моля идеального двухатомного газа, имеющего начальную температуру
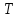 , его объем увеличился в 2 раза. Для этого к газу надо подвести количество теплоты, равное
, его объем увеличился в 2 раза. Для этого к газу надо подвести количество теплоты, равное1)
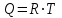
2)
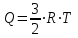
3)
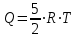
4)
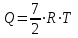
:4
6. [Уд1] (ВО1) Двум молям водорода сообщили 580 Дж теплоты при постоянном давлении. При этом его температура повысилась на … К.
1) 10
2) 27
3) 38
4) 45
:1
7. [Уд1] (ВО1) У водорода, взятом в количестве 2 моль при постоянном давлении, температура повысилась на 10 К. При этом ему сообщили количество теплоты, равное … Дж.
1) 370
2) 580
3) 640
4) 925
:2
8. [Уд1] (ВО1) Водороду, имеющему постоянный объем, сообщили 580 Дж теплоты и его температура повысилась на 10 К. Количество вещества составляет … моль.
1) 2,8
2) 3,5
3) 4,7
4) 6,8
:1
9. [Уд] (ВО1). Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты
 . На работу газа расходуется часть теплоты
. На работу газа расходуется часть теплоты 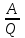 , равная
, равная 1) 0,40
2) 0,75
3) 0,60
4) 0,25
:1
10. [Уд] (ВО1). Двухатомному идеальному газу в результате изобарического процесса подведено количество теплоты
 . На работу газа расходуется часть теплоты
. На работу газа расходуется часть теплоты 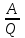 , равная
, равная1) 0,41
2) 0,73
3) 0,56
4) 0,29
:4
11. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изобарического и кругового процессов в идеальных газах, приведены под номерами:
1) Q= U+ A
2) 0 = U + A
3) Q = U
4) Q = A
:1, 4
12. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изохорического и изотермического процессов в идеальных газах, приведены под номерами:
1) Q= U+ A
2) 0 = U + A
3) Q = U
4) Q = A
:3, 4
13. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изохорического и изобарического процессов в идеальных газах, приведены под номерами:
1) Q= U+ A
2) 0 = U + A
3) Q = U
4) Q = A
:1, 3
14. [Уд1] (ВО1) Работа, совершаемая в изотермическом процессе, определяется формулой
1)
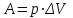
2)
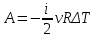
3)
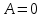
4)
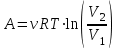
:4
15. [Уд1] (ВО1) Работа, совершаемая газом в изохорическом процессе, определяется формулой под номером
1)
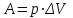
2)
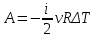
3)
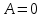
4)
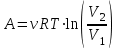
:3
16. [Уд1] (ВО) Внутренняя энергия идеального двухатомного газа выражается формулой
1)
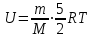
2)
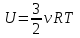
3)
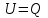
4)
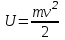
: 1
17. [Уд] (ВО1). Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты
 . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты  , равная
, равная 1) 0,40
2) 0,75
3) 0,60
4) 0,25
:3
18. [Уд1] (ВО1) При изобарическом процессе в идеальном газе его объем возрос в два раза. Внутренняя энергия газа при этом
1) увеличилась в два раза
2) уменьшилась в два раза
3) не изменилась
4) увеличилась в 4 раза
:1
19. [Уд1] (ВО1) Один моль одноатомного идеального газа, имеющий начальную температуру T = 250 К, нагрели изобарически. При этом его объем увеличился в 2 раза. Изменение внутренней энергии
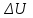 газа равно … кДж.
газа равно … кДж.1) 2,7
2) 3,1
3) 3,8
4) 4,5
: 2