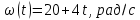Файл: Кластер с014 п графические задачи, кластеры Кинематика вращательного движения твердого тела. П ( 15 шт).docx

Кластер с014 П Графические задачи, кластеры Кинематика вращательного движения твердого тела.П ( 15 шт)

1
. [Уд3] (ВОМ) Диски, угловые ускорения которых направлены вверх, представлены под номерами (стрелки на рисунках указывают направления вращения):

1) 1

2) 2

3) 3

4) 4

:1,4

2
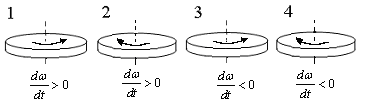
. [Уд1] (ВО1) На рисунке стрелками показаны направления вращения дисков и указано, как изменяется угловая скорость со временем. Неправильно показано направление углового ускорения на рисунке под номером …

1) 1

2) 2

3) 3

4) 4

:2

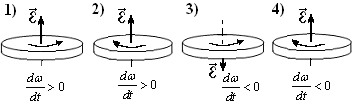
3. [Уд1] (О) Верно указано направление вектора углового ускорения тела, совершающего равноускоренное вращение на рисунке под номером …



:3

4 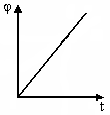. [Уд3] (ВОМ) На графике представлена зависимость угла поворота φ вращающегося по окружности тела от времени t. Начальная угловая скорость . Номера утверждений, справедливых для этого движения:

1) угловая скорость вращения постоянна

2) линейная скорость движения равномерно возрастает

3) нормальное ускорение постоянно по величине

4) угловое ускорение постоянно и не равно нулю

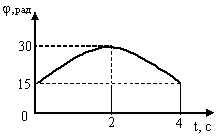
: 1,3,4

5. [Уд1] (О) На графике представлена зависимость угла φ поворота вращающегося тела от времени t. Угловая скорость вращения тела равна нулю в момент времени t = … с.

:2

6 . [Уд1] (О) На графике представлена зависимость угла φ поворота вращающегося тела от времени

---

t. Тело ускоренно вращается в течение … с

:2

7 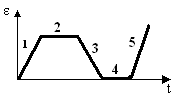. [Уд1] (О) На рисунке приведен график зависимости модуля углового ускорения вращающегося тела от времени. Вращение тела с постоянной угловой скоростью соответствует участку графика под номером …

:4

8 . [Уд1] (О) На рисунке приведен график зависимости модуля углового ускорения вращающегося тела от времени. Равноускоренное вращение тела соответствует участку графика под номером …

:2

9 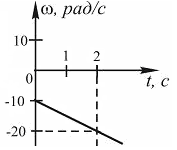. [Уд1] (ВО1) Тело вращается вокруг неподвижной оси. Зависимость проекции угловой скорости от времени показана на рисунке. Проекция углового ускорения тела равна … рад/с².

1) – 0,5

2) 0,5

3) – 5

4) 5

:3

1 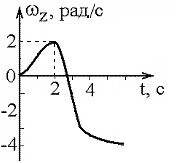0. [Уд1] (ВО1) Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. Угловое ускорение точки в момент времени t₁= 2 с равно … рад/с².

1) 1

2) 2

3) 0

4) – 1

:3

1 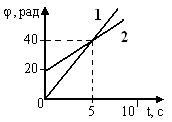1. [Уд1] (ВО1) На графике представлены зависимости угла φ поворота двух вращающихся по одной окружности тел от времени t. Сравнивая величины угловых скоростей, можно утверждать, что

1) скорость второго тела в два раза больше, чем у первого

2) скорость первого тела в два раза больше, чем у второго

3) скорости обоих тел одинаковы

4) конкретного ответа дать нельзя

:2

1 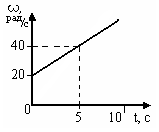2. [Уд1] (О) На графике представлена зависимость угловой скорости ω, вращающегося тела, от времени t. Величина углового ускорения равна … рад/с².

:4

1

---

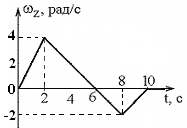
3. [Уд1] (ВО1) Твердое тело начинает вращаться вокруг оси ОZ с угловой скоростью, проекция которой изменяется со временем, как показано на графике. Максимальная величина углового ускорения соответствует интервалу времени от …

1) 0 до 2 с

2) 2 с до 6 с

3) 6 с до 8 с

4) 8 с до 10 с

:1

1 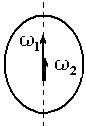4. [Уд1] (ВО1) На рисунке показаны начальная ω₁=10 рад/с и конечная ω₂=5 рад/с скорости вращения абсолютно твердого тела для интервала времени Δt=10 с. Про величину и направление углового ускорения можно сказать, что

1) ε= 1 рад/с, направлено вверх

2) ε= 1 рад/с, направлено вниз

3) ε= 0,5 рад/с, направлено вверх

4) ε= 0,5 рад/с, направлено вниз

:4

1 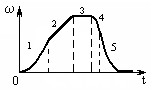5. [Уд1] (О) Твердое тело начинает вращаться вокруг оси ОZ. Проекция угловой скорости изменяется во времени, как показано на графике. Положительную и постоянную во времени проекцию углового ускорения на ось вращения тело имеет на участке, обозначенном на рисунке номером …

:2

---

Сингл S014 П Кинематика вращательного движения твердого тела. Аналитические задачи, П (s014, 15 шт)

1. [Уд1] (О) Вектор, равный по модулю углу поворота твердого тела и направленный вдоль оси вращения, называется … перемещением тела.

:угловым

2. [Уд1] (О) Направление вектора углового перемещения тела связано с направлением вращения тела правилом … буравчика.

:правого

3. [Уд1] (ВО1) При вращательном движении тела вокруг оси из векторов, являющихся кинематическими характеристиками движения, при любом характере вращения сонаправленными будут вектора

1) ,

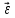
2) ,

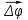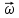
3) ,

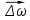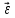
4) все вектора направлены одинаково при любом движении

:2

4. [Уд3] (ВОМ) При вращательном движении тела вокруг оси из векторов, являющихся кинематическими характеристиками движения, при вращении могут быть направлены в противоположные стороны вектора следующих пар:

1) ,

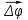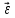
2) ,

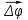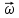
3) ,

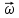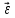
:1,3

5. [Уд1] (ВО1) Вектор угловой скорости материальной точки определяется формулой

1)

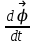
2)

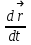
3)

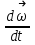
4)

---

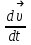
:1

6. [Уд1] (ВО1) Вектор углового ускорения материальной точки определяется формулой

1)

2)

3)

4)

:3

7. [Уд1] (О) Частица движется вдоль окружности радиусом R= 1м в соответствии с уравнением 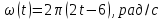. Время движения до остановки равно … сек.

:3

8. [Уд1] (ВО1) Проекция угловой скорости тела на ось вращения зависит от времени согласно уравнению 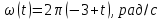. Проекция углового ускорения при этом движении равна

1) 2π

2) –2π

3) 6π

4) – 6π

:1

9. [Уд1] (ВО1) Частица движется вдоль окружности радиусом R = 1м в соответствии с уравнением 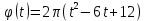, где φ – в радианах, t–в секундах. Проекция угловой скорости через 2 с после начала движения равна

1) 2π

2) –2π

3) 4π

4) -4π

:4

1 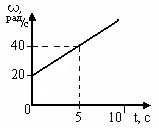0. [Уд1] (ВО1) На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Уравнение, верно отражающее зависимость угловой скорости от времени, имеет вид

1)

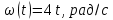
2)

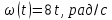
3)

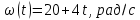
4)

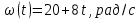
:3

1 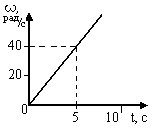1. [Уд1] (ВО1) На графике представлена зависимость угловой скорости тела, вращающегося вокруг неподвижной оси, по окружности, от времени t.

Уравнение, верно отражающее представленную зависимость, имеет вид

1)

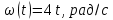
2)

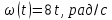
3)

---