ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задачи по курсу «Основы оптимального управления»
Вариант 1.
Движение управляемой системы определяется уравнениями:
;
(1)при начальных условиях:
. (2)Требуется определить управление u , при котором функционал
(3) принимает минимальное значение.Правый конец траектории свободен, а момент
выбирается в процессе решения задачи.Записать необходимые условия оптимальности на основе
методов вариационного исчисления.
Вариант 2.
Движение ЛА определяется уравнениями:
;
. (1)Заданы начальные условия:
. (2)Требуется определить управление
, минимизирующее
. (3)Момент времени T задан. Координаты
и 
произвольны.Записать необходимые условия оптимальности на основе методов вариационного исчисления.
Вариант 3
Возмущенное движение крена определяется уравнениями:
; (1)
.
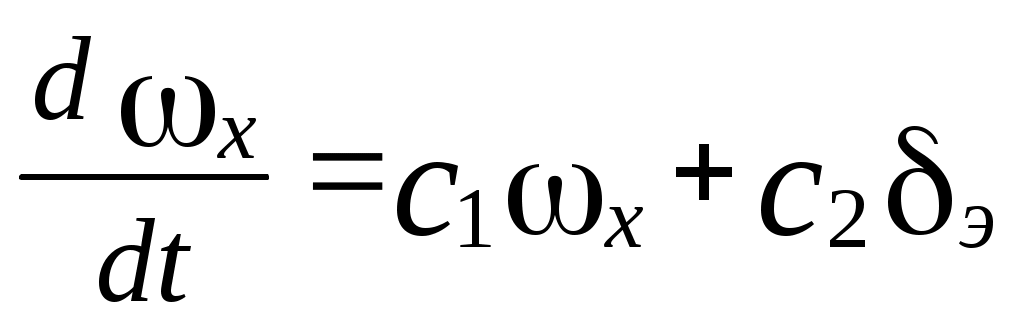
Заданы начальные и граничные условия:
при
, 
, 
; (2)при
, 
. (3)Момент
произволен.Требуется определить управление
, обеспечивающее минимум
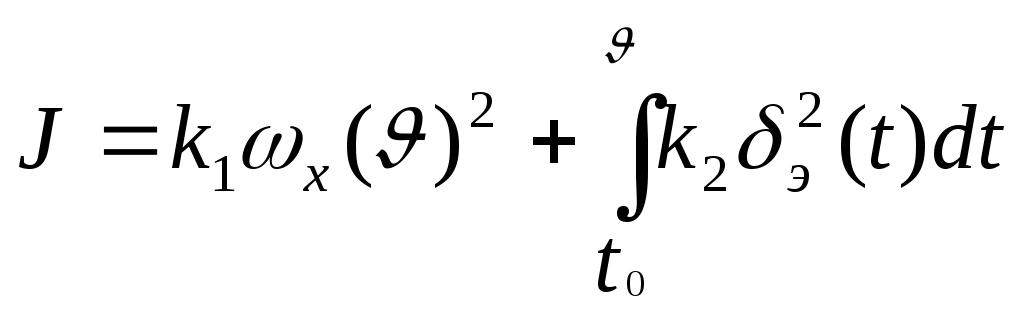. (4)Записать необходимые условия оптимальности на основе методов вариационного исчисления.
.Вариант №4
Движение ЛА определяется уравнениями:
; 
; (1)
; 
.Заданы начальные условия:
, 
, 
; 
, 
. (2)При
заданы граничные условия:
, 
. (3)Момент окончания управляемого движения
задан.Требуется найти управление
, минимизирующее
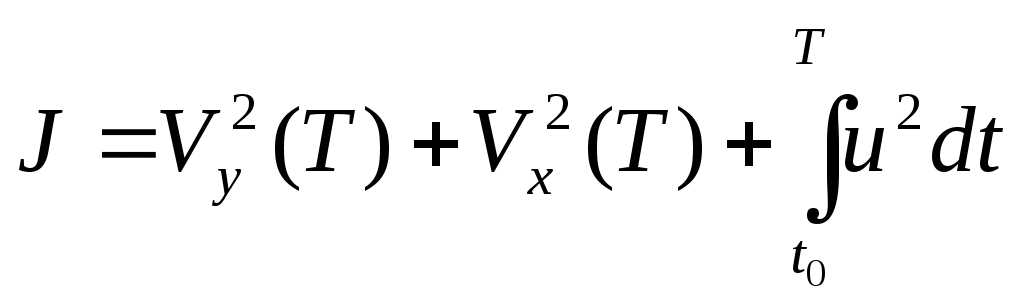. (4)Записать необходимые условия оптимальности для решения задачи (1)-(4) на основе методов вариационного исчисления.
Вариант №5
Возмущенное движение ЛА в горизонтальной плоскости определяются уравнениями:
; (1)
.Заданы начальные и граничные условия:
, 
, 
; (2)
. (3)Момент окончания движения
произволен.Требуется найти управление
, обеспечивающее минимум:
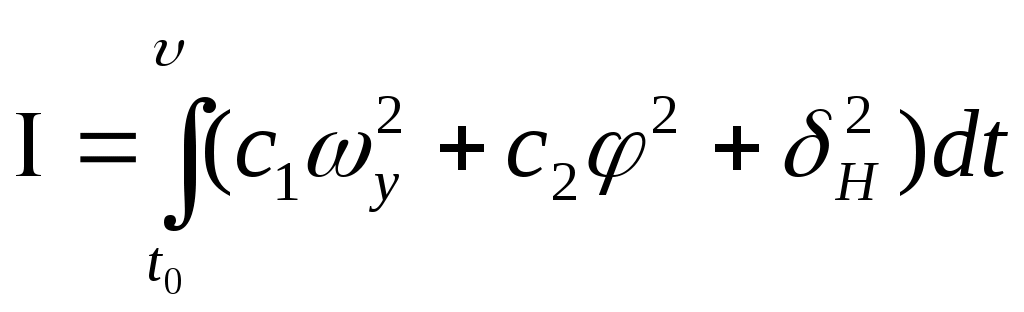. (4)Вариант №6
Первый этап продольного возмущенного движения определяется
уравнениями:
;
; (1)
.Заданы начальные и граничные условия:
, 
, 
, 
; (2)
, 
. (3)Требуется найти управление
, обеспечивающееминимум:
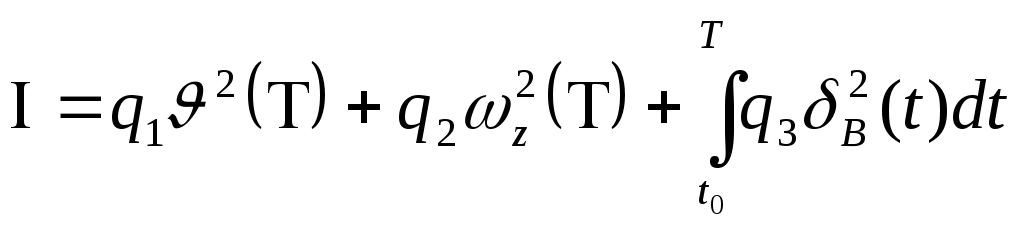. (4)Момент
задан.
Записать необходимые условия оптимальности на основе методов вариационного исчисления.
Вариант №7
Движение ЛА определяется уравнениями
; (1)
,где g – ускорение силы тяжести.
Заданы начальные и граничные условия:
, 
, 
; (2)
, 
. (3)Требуется определить управление
, обеспечивающееминимум
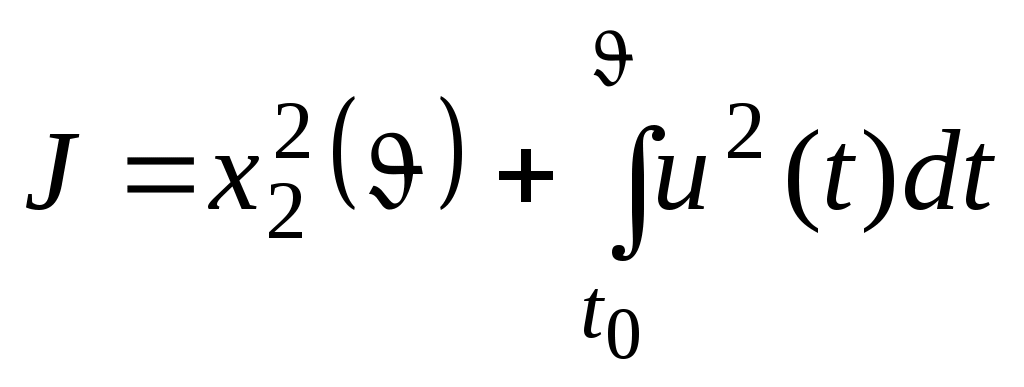. (4)Момент
произволен.Записать необходимые условия оптимальности на основе методов вариационного исчисления.
Вариант №8
Движение системы определяется уравнениями:
; (1)
.Заданы начальные условия:
при
, 
, 
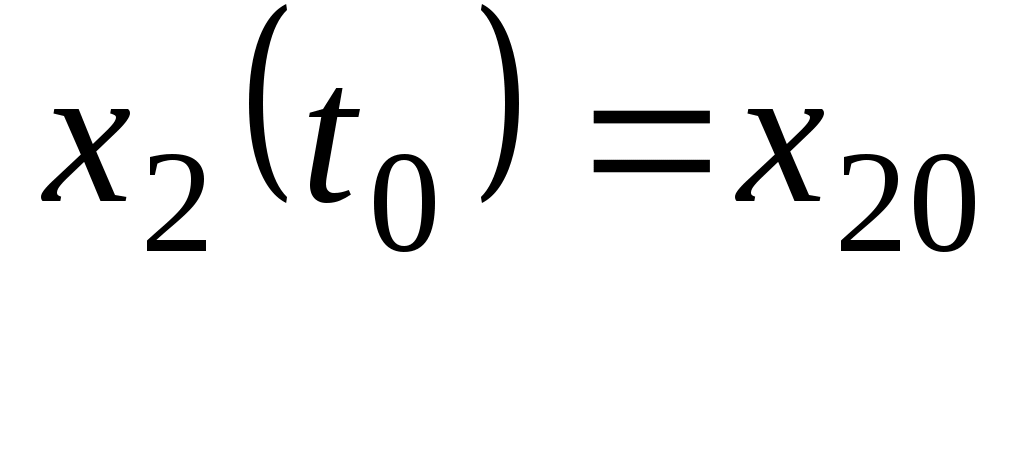. (2)Требуется найти управление
, обеспечивающееминимум
. (3)Момент
произволен, правый конец траектории свободен.Записать необходимые условия оптимальности на основе методов вариационного исчисления.
Вариант №9
Движение крена определяется уравнениями:
; (1)
.Заданы начальные условия:
, 
, 
. (2)Момент окончания движения
задан, правый конец траекториисвободен.
Требуется определить управление
, минимизирующее
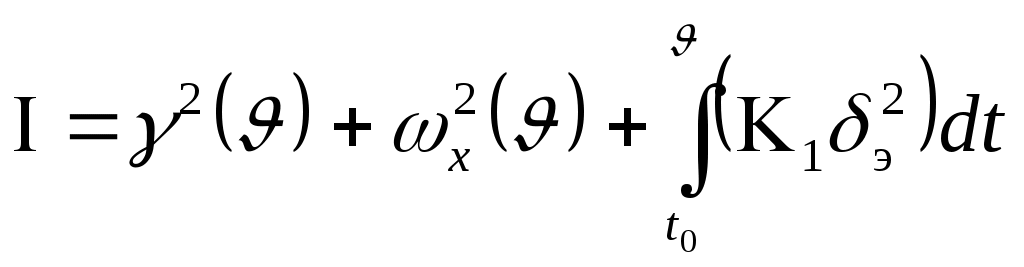. (3)Записать необходимые условия оптимальности на основе методов
вариационного исчисления.
Вариант 10
Движение ЛА в полярной системе координат определяется уравнениями:
;
, (1)где
, 
- управление.Заданы начальные условия:
, 
, 
. (2)На правом конце траектории выполняется условие:
, 
. (3)Момент окончания управляемого движения
произволен.Требуется найти управление
, при котором критерий
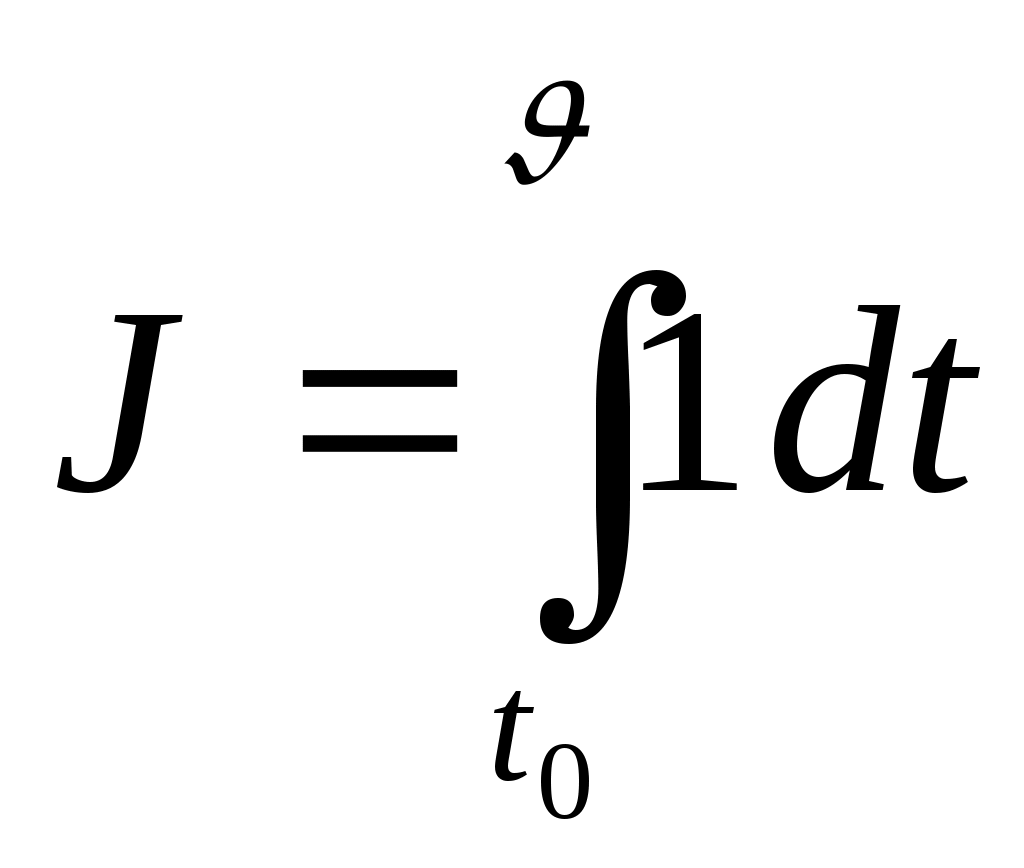(4)принимает минимальное значение.
Записать необходимые условия оптимальности для решения задачи (1)-(4) на основе методов вариационного исчисления.
Вариант №11
Движение ЛА в горизонтальной плоскости определяется уравнениями: