Файл: Задача 3 Анализ электрических цепей с индуктивно связанными элементами.docx
Добавлен: 03.12.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
(наименование института полностью)
Кафедра «Электроснабжение и электротехника»
(наименование)
13.03.02. Электроэнергетика и электротехника
(код и наименование направления подготовки / специальности)
Цифровые технологии в электроэнергетике
(направленность (профиль) /специализация)
Практическое задание № 3
по учебному курсу «Теоретические основы электротехники 1»
Вариант 2.10
Обучающийся Д.В. Бодров
(И.О. Фамилия)
Группа ЭЭТб-2107а
Преподаватель С.В. Шлыков
(И.О. Фамилия)
Тольятти 2023
Задача №3 «Анализ электрических цепей с индуктивно связанными элементами»
В заданной, согласно варианту, расчетной электрической цепи необходимо:
1. Определить активное, реактивное и полное сопротивления расчетной электрической цепи c индуктивно- связанными элементами относительно входных зажимов.
2. Рассчитать мгновенное значение напряжения ????(????)на входных зажимах цепи c индуктивно-связанными элементами.
3. Определить комплексное напряжение ????????????на участке электрической цепи c индуктивно-связанными элементами.
4. Найти активную, реактивную и полную мощности в электрической цепи c индуктивно-связанными элементами, а также реактивную мощность обмена.
5. Построить временные зависимости напряжения ????(????)и тока ????(????) по найденным законам изменения.
Задача №3
Исходные данные расчетной электрической цепи постоянного тока
Параметры электрической цепи: R1 = 100 Ом, R2 = 10 Ом, С1 = 90 мкФ, L
1 = 300 мГн, L2 = 200 мГн, L3 = 450 мГн, М12 = 260 мГн, М13 = 320 мГн ???? = 300 рад/с и ток в неразветвленной цепи равен I = 3 А.
Конфигурация расчетной электрической цепи изображена на рис. 1.
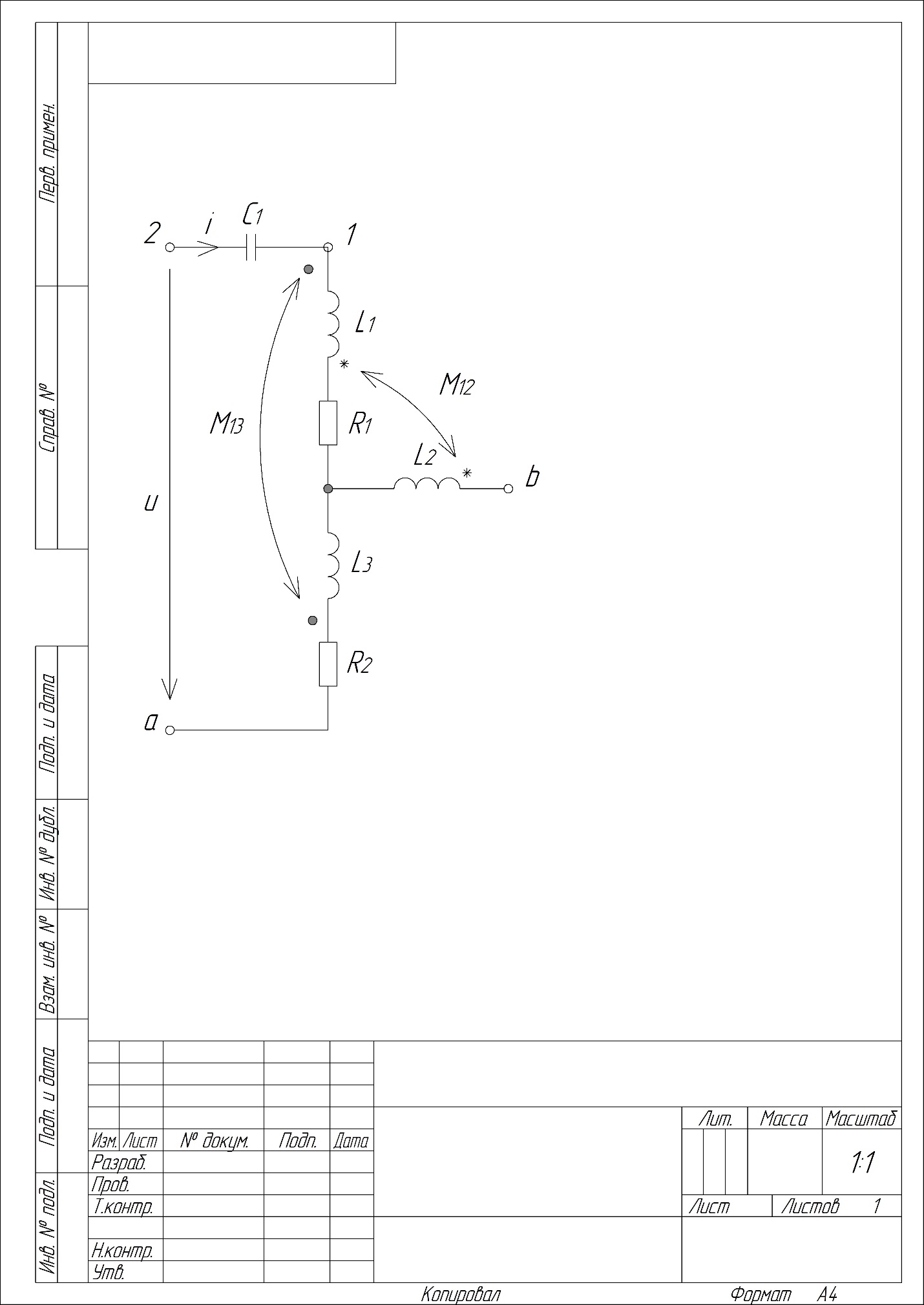
Рис. 1. Расчетная электрическая цепь
Решение
-
Определим сопротивления реактивных элементов, которые проявляют зависимость от частоты тока по формуле 1
| xL1 =  L1 = 300 300 L1 = 300 300 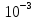 = 90 Ом = 90 ОмxL2 =  L2 = 300 200 L2 = 300 200 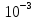 = 60 Ом = 60 ОмxL3 =  L3 = 300 450 L3 = 300 450 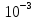 = 135 Ом = 135 ОмxM12 =  M12 = 300 260 M12 = 300 260 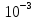 = 78 Ом = 78 ОмxM13 =  M13 = 300 320 M13 = 300 320 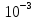 = 96 Ом = 96 ОмxC2 = 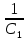 = = 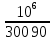 = 37,037 Ом. = 37,037 Ом. | (1) |
Ток, протекающий по электрической цепи с индуктивно связанными элементами L1 и L3, которые соединены последовательно и имеют встречное включение. Данный тип включения получается в том случае, если ток втекает в разноимённые зажимы индуктивностей L1 и L3, которые обозначены точками (рис. 1). Ситуация, когда ток протекает по элементам с одноимёнными зажимами, может наблюдаться с индуктивностями L1 и L2, где одноименные зажимы обозначены звездочками. Для замкнутого участка цепи запишем выражение комплексного сопротивления с индуктивно связанными элементами (формула 2):
| Z = R1 + R2 + j(xL1 + xL3 - xC1 – 2 xM13) = = 100 +10 + j(90 + 135 – 37,037 – 2 96) = 110 – j4,037 Ом. | (2) |
Найдем активное, реактивное и полное сопротивления цепи синусоидального тока (формула 3):
| R = Re(Z) = 110 Ом, x = Im(Z) = - 4,037 Ом, z = 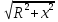 = = 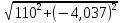 = 110,074 Ом. = 110,074 Ом. | (3) |
-
Найдем мгновенное напряжение на входных зажимах цепи синусоидального тока, воспользовавшись законом Ома в комплексной форме. Полагая, что начальная фаза комплексного тока I равна нулю, то комплекс входного напряжения U найдем по формуле 4
| U = I Z = 3 (110 – j4,037) = 250 В. | (4) |
По найденному комплексу напряжения запишем мгновенное значение напряжения по формуле 5:
| ψU= arg(U) = - 0,04 рад, U = 330,222 В, u(t) = 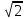 U sin(t + ψU) = U sin(t + ψU) == 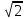 330,222 sin(300t – 0,04) 467,004 sin(300t -2,102) В. 330,222 sin(300t – 0,04) 467,004 sin(300t -2,102) В. | (5) |
-
Определим комплекс напряжения Uab на участке электрической цепи между узловыми точка «a» и «b». Необходимо применить II закон Кирхгофа для выделенного контура, где указаны направления напряжений на участках цепи согласно условно принятому направлению тока. Как видно (рис. 2), количество напряжений в выделенном контуре равно пяти, которые все включены в уравнение (формула 6):
| Uab + UR2 + UL3 – UM12 – UM13 = 0 | (6) |
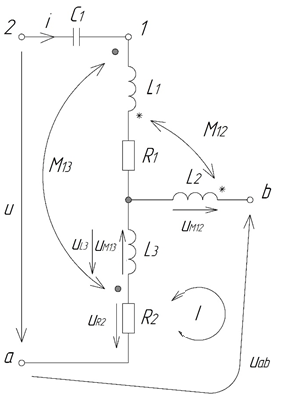
Рис. 2. Нахождение напряжения на участке электрической цепи
Используя записанное выше уравнение (формула 6), получим уравнение в комплексной форме, каждое из слагаемых которого распишем через комплекс тока I (формула 7):
| U ab + R2 I + jxL3 I – jxM12 I - jxM13 I = 0 отсюда получим: U ab = [-R2 – j ( xL3 - xM12 - xM13)] I | (7) |
Подставим числовые значения в уравнение, разрешенное относительно комплексного напряжения U ab (формула 8):
| U ab = [-10 – j (135 - 78 - 96)] 3 = - 30 + j117 В. | (8) |
-
Найдем значения активной, реактивной и полной мощностей расчетной электрической цепи с индуктивно связанными элементами (формула 9):
P = I2 (R1 +R2) = 32 (100 + 10) = 990 Вт,
Q = I2 (xL1 + xL3 - xC1 – 2 xM13) =
= 32 (90 + 135 – 37,037 – 2 96) = - 36,333 вар,
S =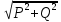 =
= 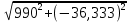 = 990,666 ВA,
= 990,666 ВA,
ΔQ = – 2 xM13 I2 = – 2 96 32 = - 1,728 квар.
(9)
-
Построим временные зависимости напряжения ????(????)и тока ????(????) по записанным законам изменения (формула 10):
| u(t) = 467,004 sin(300t -2,102) В, i(t) = 3  sin(300t) А. sin(300t) А. | (10) |
Строим временные зависимости напряжения и тока (рис. 3).
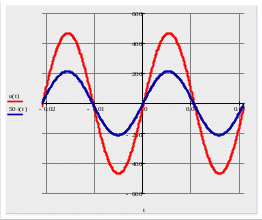
Рис. 3. Временные зависимости ????(????)и ????(????)