Шаг квантования:



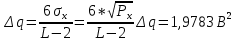
Пороги квантования:

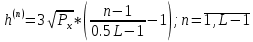
n	0	1	2	3	4	5	6	7	8
h(n), В		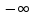-5.935	-3.9567	-1.9783	0	1.9783	3.9567	5.935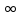

Уровни квантования:

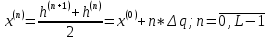
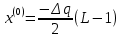
n	0	1	2	3	4	5	6	7
x(n), В	-6.9242	-4.9458	-2.9675	-0.9892	0.9892	2.9675	4.9458	6.9242

Средняя квадратичная погрешность квантования (мощность шума квантования):

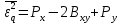
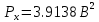
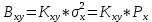
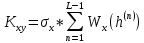
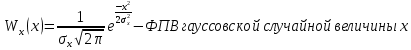
h(n)	-5.254	-3.503	-1.751	0	1.751	3.503	5.254
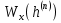	0,0022	0.0273	0,1255	0,202	0,1255	0.0273	0,0022

---

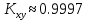
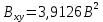
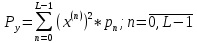
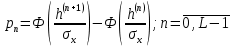
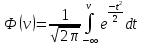
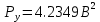
Мощность шума квантования равна:

2. 
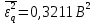
   построить в масштабе характеристику квантования.
   

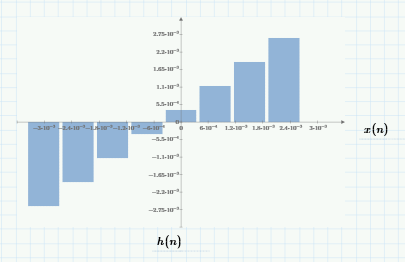
Рисунок 4 - Характеристика квантования

5. 
   Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе двоичного ДКС:
   

1. 
   рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность двоичного дискретного источника;
   

Распределение вероятностей:

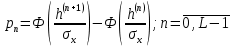
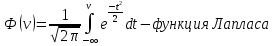
n	0	1	2	3	4	5	6	7
Pn	0,0013	0,0214	0,1359	0,3413	0,3413	0,1359	0,0214	0,0013

Энтропия:



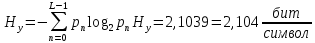
Производительность в ДКС:



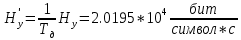
Максимальная энтропия для источника дискретных сообщений:



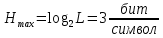
Избыточность последовательности источника:

---

2. 
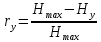
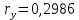
   построить в масштабе графики, рассчитанных закона и функции распределения вероятностей.
   

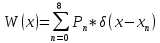
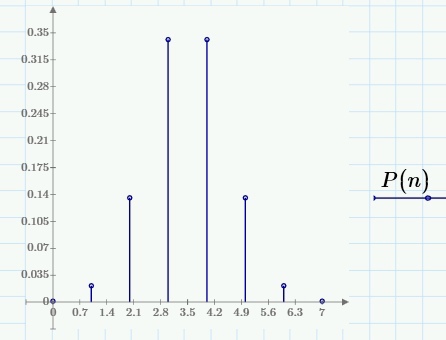
Рисунок 5 - График закона распределения вероятности



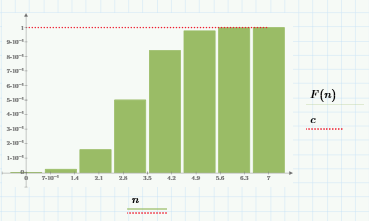
Рисунок 6 - График функции распределения вероятности

6. 
   Закодировать значения двоичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода; кроме того:
   

Получаем:

x⁽⁰⁾→0→000 x⁽⁴⁾→4→100

x⁽¹⁾→1→001 x⁽⁵⁾→5→101

x⁽²⁾→2→010 x⁽⁶⁾→6→110

x⁽³⁾ →3→011 x⁽⁷⁾→7→111

Таблица кодовых расстояний:

	000	001	010	011	100	101	110	111
000	0	1	1	2	1	2	2	3
001	1	0	2	1	2	1	3	2
010	1	2	0	1	2	3	1	2
011	2	1	1	0	3	2	2	1
100	1	2	2	3	0	1	1	2
101	2	1	3	2	1	0	2	1
110	2	3	1	2	1	2	0	1
111	3	2	2	1	2	1	1	0

---

1. 
   рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ;
   

Ширина спектра сигнала ИКМ:

7. 
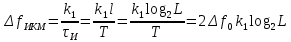
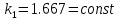
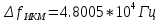
   Полагая, что для передачи ИКМ сигнала по НКС используется гармонический переносчик:
   

1. 
   рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра;
   

---

Сигнал ДЧМ представляется в виде:



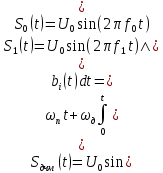
Где ω_п – частота переносчика, ω_д – девиация частоты.



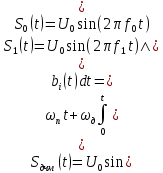
Разложение сигнала в ряд по гармоническим составляющим:



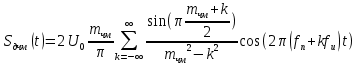
Где 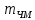– индекс частотной модуляции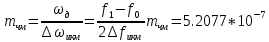



Bычислим ширину спектра ДЧМ:



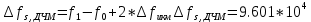
При неизвестной амплитуде 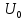вычисляют нормированный спектр: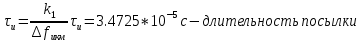

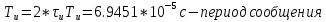
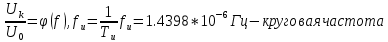
2. 
   построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра.
   

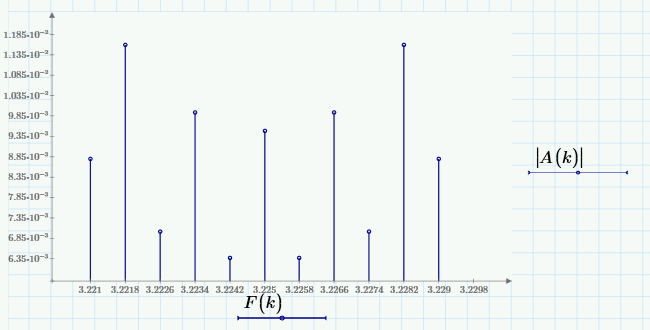
Рисунок 7 - График нормированного спектра сигнала ДЧМ

Значения нормированного спектра

8. 
   Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношения сигнал-шум:
   

1. 
   рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС;
   

---

Смотрите также файлы

• Тема урока Жиры.ppt

• Программа 2023 содержание введение.docx

• Реферат написание реферата, как учебный вид деятельности, предполагает внеаудиторную, самостоятельную учебную работу студента по рекомендуемой преподавателем теме..docx

• Коррекция и развитие.pptx

• Занятие для обучающихся 89 классов по теме День детских общественных объединений.doc