Такие таблицы помогают детям лучше понимать математическую речь, лучше ориентироваться в терминах. Работа с такими таблицами готовит учеников к решению уравнений. Работа с таблицами нравится ученикам, поэтому она также нашла свое место на моих уроках математики.

5. 
   При повторении изученного материала по теме «Признаки делимости», предлагаю таблицу
   

1,2	3,2	4,2	5,5	72
1,8	2,8	5,6	0,40	2,7
2,45	1,62	6,4	0,6	0,54
3,10	0,2	4,05	1,02	8,1
0,36	2,1	2,25	4	0,18
4,8	8,3	5,05	1,4	6,3

Предлагаются задания:

1) Выберите из таблицы числа, которые делятся на 2 (3,5 и т.д.)

2) Разделите числа из первого столбика на 5 (2, 3)

3) Уменьшите числа последнего столбика в 9 раз.

4) Найдите «лишнее» число во втором столбике.

5) Найдите числа, которые не использовали
А теперь перейду непосредственно е практико-ориентированным задачам.

Следующую задачу можно предложить поработать по материалам огэ в разных классах. По изучению соответствующих тем составлять вопросы.

Примеры (5-11 классы).



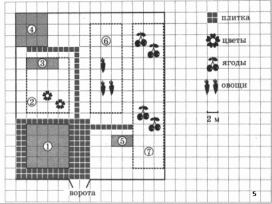
На плане изображен дачный участок по адресу: СНТ Рассвет, ул. Морская, 7 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Въезд и выезд осуществляется через единственные ворота. Площадь, занятая жилым домом, равна 64 кв. м. Помимо жилого дома, на участке есть баня, к которой ведет дорожка, выложенная специальным садовым покрытием. Между жилым домом и баней находится цветник с теплицей. Теплица отмечена на плане цифрой 3.

---

Напротив жилого дома находится бак с водой для полива растений, за ним плодово-ягодные кустарники. В глубине участка есть огород для выращивания овощей, отмеченный цифрой 6. Все дорожки внутри участка имеют ширину 1 м и застелены садовым покрытием, состоящим из плит размером 1м х 1м. Площадка вокруг дома выложена плитами такого же размера, но другой фактуры и цвета. К дачному участку проведено электричество. Имеется магистральное газоснабжение.

Вопросы для устной работы:

1. 
   Какими цифрами на плане обозначены: жилой дом, цветник, бак с водой, баня. Назовите получившееся число.
   
2. 
   Найдите площади этих объектов.
   
3. 
   На сколько площадь занятая под ягоды, больше площади занятой под овощи?
   

Рассмотрим приемы решения практико-ориетированных задач

(см. слайд):

Разбор задач

1. 
   Задачи о дачном участке
   
2. 
   Задачи о земледелии в горных районах
   
3. 
   Задачи о мобильном интернете и тарифе
   
4. 
   Задачи о теплице
   
5. 
   Задачи про шины
   
6. 
   Задачи про форматы листов
   

---

Задача 2. Показания счётчика электроэнергии 1 марта составляли 32767 киловатт-часов, а 1 апреля— 32965 киловатт-часов. По текущему тарифу стоимость 1 киловатт-часа электроэнергии составляет 3 рубля 40 копеек. Сколько нужно заплатить за электроэнергию за январь?

Одна из распространённых ошибок при решении задачи про электроэнергию — просто умножить показания января на цену электроэнергии. Школьники получают при этом величину, превосходящую сто тысяч рублей, но не могут поймать себя на ошибке, так как не чувствуют величину этого числа. Важно привить школьникам умение анализировать полученный в задаче ответ с точки зрения здравого смысла.

Задача 3. Установите соответствие между величинами и их возможными значениями. К каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

ВЕЛИЧИНЫ		ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) площадь почтовой марки Б) площадь письменного стола В) площадь города Санкт-Петербург Г) площадь волейбольной площадки		1) 362 кв. м 2) 1,2 кв. м 3) 1399 кв. км 4) 5,2 кв. см

 

Для её решения не нужно заучивать точные значения подобных величин. Достаточно привыкать к чувству порядка величины, изучая математику, физику, другие предметы.

Задача 4. На рисунке изображены автобус и автомобиль. Длина автомобиля равна 4,2 м. Какова примерная длина автобуса? Ответ дайте в сантиметрах.



 

Часто это сбивает ребят, они не понимают, как решать такую задачу. Необходимо подчеркнуть, что в задаче просят оценить именно примерную длину, искать точное значение не требуется. Также важно обратить внимание школьников на единицы измерения, в которых необходимо дать ответ: длина автомобиля дана в метрах, а ответ нужно указать в сантиметрах. 

2. Чтение текста

Один из первых и самых ключевых навыков функциональной грамотности в математике — чтение сложных текстов, из которых не всегда очевидно, что именно требуется в задаче. К сожалению, этой теме уделяется мало внимания, особенно в старших классах. Статистика проведения ЕГЭ говорит о том, что даже в очень простых задачах школьники допускают обидные ошибки, неправильно читая условия задач и находя ответ не на тот вопрос, который предлагался в задаче. Например, в задаче на поиск меньшего корня квадратного уравнения школьники невнимательно читают условие и записывают в ответ значение большего корня. В 5-м и 6-м классах важно научить детей гибкому чтению на уроках математики.

---

Важным признаком того, что условие прочитано неверно, может служить очень сложное решение или «некрасивый» ответ в задаче.

Обсудим задачу-шутку, которая хорошо иллюстрирует, как важно внимательно читать условие.

Задача 1. Представьте, что вы капитан авиалайнера, на котором путешествуют 300пассажиров. Этот самолет летит со скоростью 30 узлов в час (один узел равен 1,852 км/ч), предполагаемое время путешествия 18 часов. Сколько лет капитану корабля?

Как правило, человек, решающий эту задачу, сразу переходит к анализу чисел и пропускает первую фразу. А именно она помогает ответить на вопрос задачи: решающему достаточно указать свой возраст.

Рассмотрим ещё один пример задачи, требующей вдумчивого чтения условия.

Задача 2. Братья Иван и Миша Ивановы играют в игру. Иван загадывает число n, имеющее ровно 7 простых делителей. Миша придумывает гладкое пятимерное многообразие, описываемое формулой степени не более чем n². Иван указывает 5 точек на этом многообразии и объявляет длины не более чем 7 отрезков, соединяющих эти точки в пространстве R25. Если выбранные точки вместе с указанными Иваном отрезками образуют жёсткую структуру второго порядка, то побеждает Миша. В противном случае мальчики меняются местами: Иван придумывает другое гладкое многообразие, проходящее через эти 5 точек, и Миша указывает 5 точек на нём. Игра продолжается, пока либо у кого-то из мальчиков не получилась жёсткая структура, либо не прошло 1003 хода — в этом случае побеждает Миша. В зависимости от n назовите фамилию победителя при правильной игре.

Задача отпугивает своим громоздким условием и сложными терминами, но на самом деле для решения задачи не требуется знаний топологии. Чтобы дать верный ответ на задачу, достаточно прочитать только первое и последнее предложения из условия. 

3.Логическая грамотность

Школьникам, которые никогда не будут использовать математику в работе, всё равно придётся принимать в жизни решения, которые будут основаны на анализе сложившейся ситуации, на анализе входных данных. Эти данные могут быть текстом договора

---

, надписью на информационном щите, инструкцией к электроприбору и так далее.

В этом блоке собраны примеры заданий, с помощью которых школьники смогут научиться отвечать на вопрос «следует ли из этой информации тот или иной вывод?».

В ОГЭ, ЕГЭ есть задачи такого характера. Вот задача из открытых источников.

Задача 1. Люди, проживающие в многоквартирном доме, решили выкупить этот дом. Они вместе хотят собрать деньги таким образом, чтобы каждый из них заплатил сумму, пропорциональную площади его квартиры. Например, мужчина, проживающий в квартире, которая занимает 1/5 площади всех квартир, должен будет заплатить 1/5 от всей стоимости здания. Выберите все верные утверждения.

A. Человек, проживающий в самой большой квартире, заплатит больше денег за каждый квадратный метр своей квартиры, чем человек из самой маленькой квартиры.

B. Зная площадь двух квартир и цену одной из них, мы можем вычислить цену второй.

C. Зная цену здания и сумму, которую заплатит каждый владелец, мы можем вычислить общую площадь всех квартир.

D. Если бы общая стоимость здания была снижена на 10%, каждый из владельцев заплатил бы на 10% меньше.

В этой задаче верны утверждения B и D, а утверждения A и C неверны.

Особенность следующей логической задачи заключается в том, что при её решении удобно использовать графическое представление.

Задача 2. Кондитер испёк 40 печений, из них 10 штук он посыпал корицей, а 20 штук он собирается посыпать сахаром (кондитер может посыпать одно печенье и корицей, и сахаром, а может вообще ничем не посыпать). Выберите утверждения, которые будут верны при указанных условиях независимо от того, какие печенья кондитер посыплет сахаром.

            

---

Смотрите также файлы

• Отчет по производственной практике (научноисследовательская работа).docx

• Император Юстинианны реформалары Орындаан Ринатова Аида.pptx

• Федеральное государственное бюджетное образовательное учреждение высшего образования калмыцкий государственный университет имени б. Б. Городовикова.docx

• Урок мужества День памяти воинов, погибших в локальных конфликтах.pptx

• Инновационные технологии в образовательном процессе доу в соответствии фгос до (из опыта работы).docx