Файл: Развитие функциональной грамотности учащихся на уроках математики через практикоориентированные задания.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 98
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
A. Найдётся печений, которые ничем не посыпаны.
B. Найдётся печений, посыпанных и сахаром, и корицей.
C. Если печенье посыпано корицей, то оно посыпано и сахаром.
D. Не может оказаться печений, посыпанных и сахаром, и корицей.
4. Незнакомый контекст
Один из классических методических подходов к классификации сложности задач заключается в том, что решение задач базового уровня — это решение задач знакомыми методами в знакомой ситуации, задачи повышенной сложности — это решение задач знакомыми методами в изменённой ситуации, а задачи высокого уровня сложности требуют применения изученных методов в незнакомой ситуации.
Задачи с незнакомым контекстом занимают значительное место в международных исследованиях качества образования, в том числе в исследовании PISA. В таких задачах описана незнакомая для человека ситуация, в которой ему необходимо применить зачастую совсем несложные математические методы. Такие задачи присутствуют и в ЕГЭ, и в экзамене за 9 класс, например, 10-я задача профильного экзамена.
Чтобы решить задачу с незнакомым контекстом, необходимо внимательно прочитать условие, вычленить существенные части математической модели и значения тех или иных переменных и дать ответ, максимально абстрагировавшись от контекста.
Задача 1. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 185 МГц. Скорость погружения батискафа v (в м/с) вычисляется по формуле v=c⋅(f−f0)/f+f0, где c=1500 м/c — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 20 м/с. Ответ дайте в МГц.
Эту задачу можно упростить, если мысленно отбросить подробности сюжета и вычленить математическую модель.
[...] испускает [...] импульсы частотой 185 МГц. Скорость погружения [...] v (в м/с) вычисляется по формуле v=c⋅(f−f0))/f+f0, где c=1500 м/c — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 20 м/с. Ответ дайте в МГц.
После такой процедуры становится понятно, что все значения переменных известны, кроме одного, и его уже несложно найти подстановкой в формулу.
Задача 2. Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65R15 (рис. A). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке Б). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр H на рисунке 2) к ширине шины, то есть 100⋅HB.

Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70R13.
1. Завод допускает установку шин с другими маркировками. В таблице приведены разрешённые размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
| 13 | 14 | 15 | |
| 165 | 165/70 | 165/65 | — |
| 175 | 175/65 | 175/65;175/60 | — |
| 185 | 185/65;185/60 | 185/60 | 185/55 |
| 195 | 195/60 | 195/55 | 195/55;195/50 |
1. На сколько миллиметров радиус колеса с шиной маркировки 205/55R14 больше, чем радиус колеса с шиной маркировки 165/65R14? Ответ округлите до десятых.
2. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых.
3. Дмитрий планирует заменить зимнюю резину на летнюю на своём автомобиле. Для каждого из четырёх колёс последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций приведены в таблице.
| Автосервис | Суммарные затраты на дорогу | Стоимость для одного колеса | |||
| Снятие колеса | Замена шины | Балансировка колеса | Установка колеса | ||
| А | 210 руб. | 60 руб. | 250 руб. | 200 руб. | 60 руб. |
| Б | 380 руб. | 55 руб. | 220 руб. | 180 руб. | 55 руб. |
Сколько рублей Дмитрий заплатит за замену резины на своём автомобиле (включая дорогу), если выберет более дешёвый вариант?
-
Работа с графическими представлениями информации
Первый тип задач: Графики
Информация, которую мы получаем, с течением времени представляется во всё более сложном виде, однако сам подход к чтению и осмыслению её не меняется — графическое представление информации бывает в виде графиков, диаграмм, схем и таблиц.
Разберём задачу №2 из профильного ЕГЭ.
Задача 1. На графике показано, как изменялась температура воздуха с 3 по 5 апреля. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия.
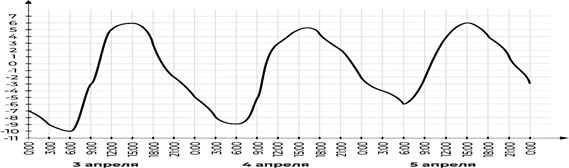
A. Найдите наименьшее значение температуры 4 апреля. Ответ дайте в градусах Цельсия.
B. В течение скольких часов температура 5 апреля была меньше 4 градусов Цельсия?
C. Найдите значение температуры 4 апреля в 3 часа дня. Ответ дайте в градусах Цельсия.
Второй тип задач:Качественный анализ графиков
Традиционно изучение графиков начинается с обсуждения практических графиков, например, графиков температуры или скорости. Но практически сразу акцент переносится на графики формальные, например, графики линейной или квадратичной функции. Типичным примером задачи на эту тему может быть следующая задача.
Задача 2. Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1;1].
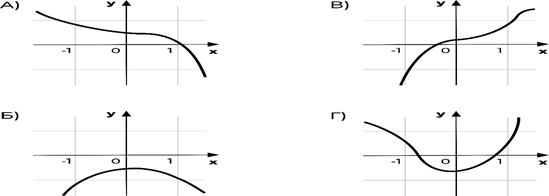
Характеристики.
-
Функция имеет точку максимума на отрезке [−1;1]. -
Функция имеет точку минимума на отрезке [−1;1]. -
Функция возрастает на отрезке [−1;1]. -
Функция убывает на отрезке [−1;1].
В последнее время к таким задачам стали добавляться задачи на анализ практических графиков, например, следующая.
Задача 3. На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси — температура двигателя в градусах Цельсия.
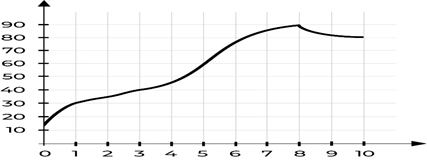
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
| Интервалы времени | Характеристики |
| 0–1 мин | Самый медленный рост температуры. |
| 1–3 мин | Температура падала |
| 3–6 мин | Температура находилась в пределах от С40∘С до С80∘С |
| 8–10 мин | Температура не превышала С30∘С |
Ещё один пример практиориентированной задачи из материалов исследования PISA. Как правило это задачи с не очень чётким условием, при их решении нужно применять и математических знания, и умение внимательно читать условие, и здравый смысл.
6. Экономика — одно из наиболее естественных приложений математики и, наоборот, один из «заказчиков» создания математики.
С такими задачами сталкивается любой ученик в реальной жизни, а как следствие — ещё и на экзаменах. Трудности, которые вызывают у многих учащихся даже несложные задачи на проценты, обычно во многом обусловлены достаточно формальным подходом к изложению темы. А ведь для решения подавляющего большинства задач на проценты достаточно понимать, что процент — это просто одна сотая часть числа. Поэтому для успешного решения задач на проценты достаточно научиться «переводить»