Файл: Вид урока Урок изучения новых знаний Тема урока Площади круга, сектора и сегмента. Цели обучения, которые достигаются на данном уроке.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Раздел: 9.4 А Окружность и круг. Длина дуги. Площади круга, сектора и сегмента | Школа: КГУ «Сычевская ООШ» | ||||
| Дата: | ФИО учителя: Абдрахманова Г.Г. | ||||
| Класс: 9 | Количество присутствующих: | отсутствующие: | |||
| Вид урока | Урок изучения новых знаний | ||||
| Тема урока: | Площади круга, сектора и сегмента. | ||||
| Цели обучения, которые достигаются на данном уроке | 9.1.1.2 выводить и применять формулу площади сектора, сегмента; | ||||
| Цели урока | Учащиеся будут:
| ||||
| Критерии оценивания |
| ||||
| Языковая цель | Учащиеся будут: - строить схематично окружность и обозначать на ней необходимые элементы; - использовать обозначения и понятия; - различать фигуры; - обсуждать и комментировать алгоритм решения задач и вывод формулы. Предметная лексика и терминология:
- площадь кругового сегмента. Серия полезных фраз для диалога и письма: -построим окружность; -отметим на окружности сектор и сегмент; -определим площади круга, сектора и сегмента используя формулу; -выразим из формулы необходимый элемент. | ||||
| Привитие ценностей |
| ||||
| Межпредметные связи | Взаимосвязь с жизнью через решение задач; география, биология. | ||||
| Навыки использования ИКТ | Использование интерактивной доски в качестве средства записи и демонстрации презентации. | ||||
| Предварительные знания | Знают понятия: круг, окружность, радиус, центральный угол, площадь треугольника. Умеют решать задачи на нахождение площади круга, площади треугольника. | ||||
| Ход урока. | |||||
| Запланированные этапы урока | Деятельность учителя | Деятельность ученика | |||
| Начало урока 2 мин | 1.Организационный момент. -проверка эмоционального фона учащихся; -проверка домашней работы - тема урока, цель обучения и критерии достижения обсуждаются с учащимися. | - определение «зоны ближайшего и дальнего развития» учащихся, ожидания к концу урока (каждый учащийся кратко пишет на стикере на столе) | |||
| Середина урока 3 мин 7 мин 12 мин Конец урока 4 мин | 2. Актуализация знаний. Фронтальная работа. Мотивация. Задача на логику «Кольцо вокруг Земли.» Образно представьте себе нашу планету, плотно стянутую кольцом по всему ее экватору. После увеличения длины окружности кольца на 10 метров, между кольцом и поверхностью земли образовался зазор определенной величины. Как Вы считаете, сможет ли человек пройти, или хотя бы протиснуться в этот зазор? Известно, что экватор имеет длину приблизительно равную 40 000 километров. Обратная связь: При выборе учениками ответа да или нет и его аргументации, учитель в диалоге делает вывод о том, насколько усвоен материал предыдущего урока. Проверяется знание формул и умение их применять. По активности обсуждения, определяется, насколько учащиеся мотивированы на изучение данной темы. 3. Изучение новой темы. Задача. На телевидении, при прогнозе погоды, используют символ облака, показанный на рисунке. 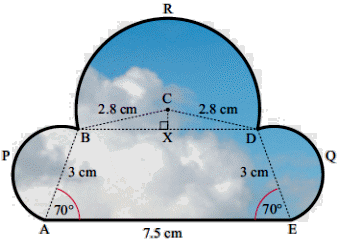 Что нам нужно знать для решения этой задачи? (проблемный вопрос) Объединяю учащихся в малые группы и предлагаю самостоятельно, зная формулу площади круга, вывести формулы площади сектора и площади сегмента. По учебнику изучают новую тему и составляют конспект вывода формул. Обратная связь: Учитель наблюдает за работай групп, оказывает помощь, отвечает на вопросы. 4. Решение задач на применение новых знаний. Каждая группа решает одну задачу и оформляет ее решение. 1) Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 см и 12 см. (Рис.1) 2)Площадь кругового сектора равна 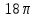 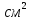 , а его центральный угол равен , а его центральный угол равен 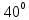 . Найти радиус сектора и площадь сегмента, опирающегося на центральный угол. (Рис.2) . Найти радиус сектора и площадь сегмента, опирающегося на центральный угол. (Рис.2)3) Хорды АВ и АС равны между собой. Образованный ими угол вписан в окружность и равен 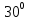 . Найдите отношение площади той части круга, которая заключена в этом угле, к площади всего круга. (Рис.3) . Найдите отношение площади той части круга, которая заключена в этом угле, к площади всего круга. (Рис.3)4) Сторона равностороннего треугольника, вписанного в окружность, равна а. Вычислите площадь отсекаемого ею сегмента. (Рис.4) ЗАДАЧА 3: Хорды АВ и АС равны между собой. Образованный ими угол вписан в окружность и равен 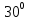 . Найдите отношение площади той части круга, которая заключена в этом угле, к площади всего круга. (Рис.3) . Найдите отношение площади той части круга, которая заключена в этом угле, к площади всего круга. (Рис.3)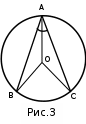 Дано: Дано:АВ=АС  ВАС= ВАС=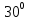 Найти: 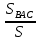 (отношение площади той части круга, которая заключена в угле  ВАС, к площади всего круга) ВАС, к площади всего круга)Решение: Отметим 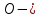 центр круга, соединим точки, образующие радиусы ВО, ОС, ОА. Для начала найдем часть круга, заключенную в угле центр круга, соединим точки, образующие радиусы ВО, ОС, ОА. Для начала найдем часть круга, заключенную в угле  ВАС, она складывается из следующих площадей фигур: ВАС, она складывается из следующих площадей фигур: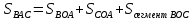  ВОС= ВОС=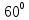 (как соответствующий центральный угол вписанному углу (как соответствующий центральный угол вписанному углу  ВАС= ВАС=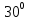 ) )Градусная мера всего круга равна 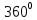 . . АОВ= АОВ= АОС (по трем сторонам: ВО=ОС как радиусы, АВ=АС по условию задачи, ОА общая сторона). Из равенства треугольников следует равенство соответствующих элементов: АОС (по трем сторонам: ВО=ОС как радиусы, АВ=АС по условию задачи, ОА общая сторона). Из равенства треугольников следует равенство соответствующих элементов: ВОА= ВОА= СОА СОА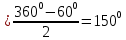 . .Достаточно найти площадь одного из равных треугольников: 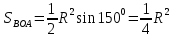 (т.к. синус второй четверти положителен) (т.к. синус второй четверти положителен)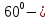 составляет составляет 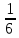 часть от всего круга, значит, если площадь круга равна часть от всего круга, значит, если площадь круга равна 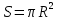 , то: , то: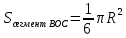 Теперь можем найти площадь части круга, заключенную в угле  ВАС: ВАС: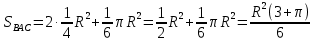 Радиус мы найти не сможем, поскольку мало данных, и для нахождения отношения площадей он нам не потребуется, давайте убедимся в этом: 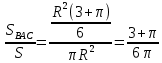 Ответ: 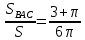 Дескриптор: -находит часть круга, заключенную в угле  ВАС, ВАС,- доказывает равенство треугольников АОВ=  АОС, АОС, - находит площадь одного из равных треугольников, -находит площадь сегмента ВОС, - находит площадь части круга, заключенную в угле  ВАС ВАСФормативное оценивание: Самопроверка по готовому решению на слайде. Прием «Светофор». Зеленый цвет- все верно, желтый- 1-2 ошибки, красный- более 2 ошибок Обратная связь: что при решении задачи вызвало затруднение? 5.Физминутка для глаз 6. Практическая работа. Деление на 3 группы «Атомы, молекулы» Еще античные философы говорили: «Не для школы учимся, а для жизни». А значит, знания, которые ребята приобретают в школе, они должны уметь применять в повседневной жизни. Давайте посмотрим, как нахождение длины окружности и площади круга помогают в повседневной жизни. Активный методобучения ЗИГЗАГ сприменениемзаданийPISA: №1 Цена пиццы В пиццерии подают две круглых пиццы одной и той же толщины, но разных размеров. Меньшая имеет диаметр 30 см и стоит 30 денег. Большая имеет диаметр 40 см и стоит 40 денег. Какую из двух пицц выгоднее покупать? Приведите ваши рассуждения. Решение (3мин) Толщина двух пицц одинаковая, поэтому вычислим площадь каждой пиццы, предполагая, что это обычный круг. Площадь круга находится по формуле (где Найдем стоимость 1 см Для пиццы 30 см она составляет Для пиццы 40 см она составляет Покупка пиццы диаметром 40 см является более выгодной. №2 Рост лишайников Одним из последствий глобального потепления является таяние льда некоторых ледников. Через двенадцать лет лед исчезает, и крошечные растения — лишайники — появляются на скалах. Во время роста лишайники образуют круги. Соотношение между диаметром круга и возрастом лишайника приблизительно определяется формулой: где 1. Используя формулу, рассчитайте диаметр лишайника через 16 лет после того, как лед растаял. 2. В какой-то год диаметр лишайника составил 42 миллиметра. Сколько лет назад растаял лед в данном месте? Приведите решение. Решение 1. Применим формулу для Через 16 лет диаметр лишайника будет14 мм. 2. По той же формуле Через 48 лет лишайник достигает диаметра 42 мм. Формативное оценивание: Взаимооценивание в группах Обратная связь: Что в вашей задаче вызвало особый интерес? Насколько пригодились знания по данной теме? Домашнее задание : из раздела «Упражнения» учебника по данной теме решить на выбор любые 2 задачи. | Решение задач. ЗАДАЧА 1: Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 см и 12 см.(Рис.1)  Дано: Дано: 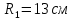 (радиус большего круга) (радиус большего круга)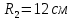 (радиус меньшего круга) (радиус меньшего круга)Найти: 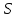 (площадь кольца) (площадь кольца)Решение: Из площади большего круга вычесть площадь меньшего круга, т.к. центры совпадают. 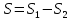 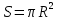 : :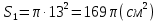 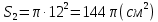 Теперь можем найти площадь кольца: 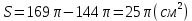 . . Ответ: 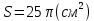 . .Дескриптор: -находит площадь большего круга; - находит площадь меньшего круга, - находит площадь кольца. ЗАДАЧА 2: Площадь кругового сектора равна 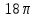 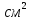 , а его центральный угол равен , а его центральный угол равен 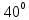 . Найти радиус сектора и площадь сегмента, опирающегося на центральный угол. (Рис.2) . Найти радиус сектора и площадь сегмента, опирающегося на центральный угол. (Рис.2)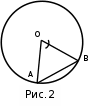 Дано: 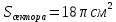 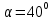 Найти: 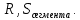 Решение: Площадь сегмента находится по формуле 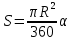 , из нее мы можем выразить радиус сектора, зная площадь сектора и градусную меру дуги сектора: , из нее мы можем выразить радиус сектора, зная площадь сектора и градусную меру дуги сектора: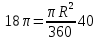 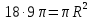 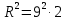 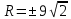 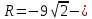 не удовлетворяет условию задачи. не удовлетворяет условию задачи.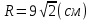 Найдем площадь  АОВ, а потом вычтем из площади сектора площадь АОВ, а потом вычтем из площади сектора площадь АОВ, тем самым найдем площадь искомого сегмента. АОВ, тем самым найдем площадь искомого сегмента.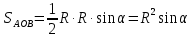 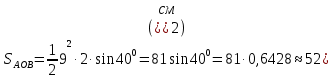 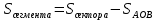 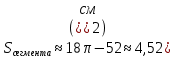 Ответ: 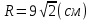 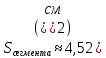 Дескриптор: -находит радиус сектора, зная площадь сектора и градусную меру дуги сектора; - находит площадь  АОВ, АОВ, -. находит площадь искомого сегмента ЗАДАЧА 4: Сторона равностороннего треугольника, вписанного в окружность, равна а. Вычислите площадь отсекаемого ею сегмента. (Рис.4) 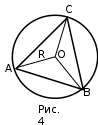 Дано: 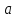 (сторона равностороннего треугольника) (сторона равностороннего треугольника)Найти: 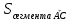 Решение: 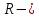 радиус описанного круга находится как радиус описанной окружности по следующей формуле: радиус описанного круга находится как радиус описанной окружности по следующей формуле: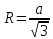 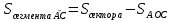 (площадь сегмента равна разности площади сектора, опирающего на угол (площадь сегмента равна разности площади сектора, опирающего на угол  АОС, и площади АОС, и площади  АОС) АОС)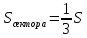 ,где ,где 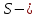 площадь круга, т.к. площадь круга, т.к.  АОС= АОС=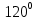 , поскольку треугольник , поскольку треугольник  АВС является равносторонним, т.е. правильным. АВС является равносторонним, т.е. правильным.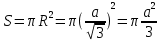 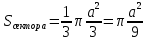 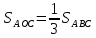 (т.к. (т.к.  АВС является равносторонним, т.е. правильным) АВС является равносторонним, т.е. правильным)А площадь правильного треугольника мы можем найти по известной нам формуле: 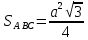 Следовательно, площадь треугольника  АОС равна: АОС равна: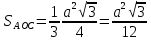 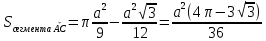 (кв.ед.) (кв.ед.)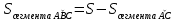 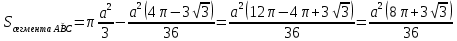 (кв.ед.) (кв.ед.)Ответ: 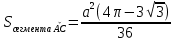 (кв.ед.) (кв.ед.)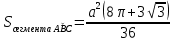 (кв.ед.) (кв.ед.)Дескриптор: -получает формулу для нахождения площади сегмента АС - находит площадь сектора - находит площадь треугольника  АОС АОС-находит площадь сегмента АС - находит площадь сегмента АВС №3.ФИГУРЫ 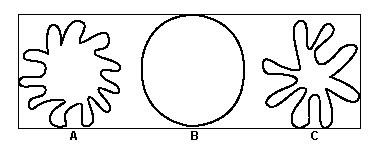 Вопрос : У какой из фигур большая площадь? Аргументируйте свое решение. Примерыответов
Это фигура с наибольшей площадью, потому что остальные могут поместиться внутри нее.
PISA Математическая грамотнос Рефлексия
| |||
| | | | |||
| | | Слайд 4 | |||
| | Слайд 5 Слайд 6 Слайд 7 Слайд 8 Слайд 9 PISA Математическая грамотность 2020 с.30 | ||||
| | | | |||
| Дополнительная информация | |||||
| Дифференциация - как вы планируете оказывать больше поддержки? Как вы планируете давать задания более способным учащимся? | Междисциплинарные связи Безопасность жизнедеятельности ИКТ связи Связи с ценностями | ||||
| | | ||||
| Оценивание - как вы планируете проверить знания учащихся? | | ||||
| Размышление | Используйте графу ниже, чтобы проанализировать Ваш урок. Ответьте на самые актуальные вопросы из графы слева о проведенном уроке. | ||||
| | |||||
| Сводная оценка Какие два аспекта прошли очень хорошо (рассмотрите преподавание и обучение)? 1: Лабораторная работа. 2: Какие два аспекта улучшили бы урок (рассмотрите преподавание и обучение)? 1: Что я узнал о классе или об отдельных учащихся на данном уроке, что я учту на следующем уроке? | |||||