Министерство образования и науки Алтайского края

краевое государственное бюджетное профессиональное образовательное учреждение

«Рубцовский аграрно-промышленный техникум»

______________________________________________________________________________

наименование учебной дисциплины
ВНЕАУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА
_________________________________________________

(наименование: реферат, доклад, практическая работа и др.)

______________________________________________________________________________________________

фамилия, имя, отчество студента


______________________________________________________________________________________________

(специальность)

______________________________________________________________________________________________

фамилия, имя, отчество преподавателя
______________________________________________________________________________________________

подпись преподавателя
Группа ________________________

Самостоятельная работа №1

Тема 1.1 Электрическое поле

Электрическое поле (статическое) — поле неподвижных, электрически заряженных тел, заряды которых не изменяются во времени.

Электрическое поле обнаруживается как силовое взаимодействие заряженных тел.

При этом различают положительные и отрицательные заряды. (виды зарядов)

Заряды одного знака отталкиваются друг от друга, разного знака притягиваются. (взаимодействие зарядов)

В основе описания свойств электрического поля лежит закон Кулона, установленный опытным путем.

Закон Кулона. Между покоящимися точечными зарядами действует сила, пропорциональная произведению зарядов, обратно пропорциональная квадрату расстояния между ними и направленная по прямой от одного заряда к другому (рис. 1.):



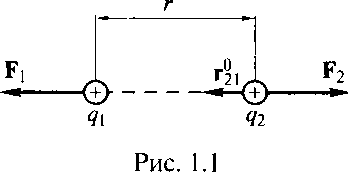
Рисунок 1


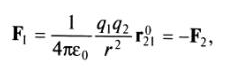
где F — сила, действующая на заряд q

r² — квадрат расстояния между зарядами q₁ и q₂

F₂ — сила, действующая на заряд q₂

r⁰₂₁ — единичный вектор, направленный от второго заряда к первому;

е₀ = 8,854 • 10-¹² Ф/м — электрическая постоянная.
Точечными зарядами можно считать заряженные тела, размеры которых малы по сравнению с расстоянием между ними.

---

Основные единицы измерения:

силы в международной системе единиц (СИ) — ньютон (Н);

заряда — кулон (Кл): 1 Кл = 1 А • с;

длины — метр (м).

Основными величинами, характеризующими электрическое поле, являются

напряженность,

электрический потенциал и

разность потенциалов, или напряжение
Напряженностью электрического поля называется мера интенсивности его сил, равная отношению силы F, действующей на пробный положительный точечный заряд q, вносимый в рассматриваемую точку поля, к значению заряда:


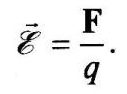
Так же как и сила F, напряженность электрического поля ε — векторная величина, т.е. характеризуется значением и направлением действия.

Основная единица измерения напряженности электрического поля в СИ — вольт на метр (В/м).

Из формулы (1.1) следует, что напряженность электрического поля точечного заряда q на расстоянии r от него равна



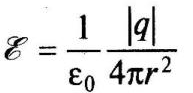
и направлена от точки расположения заряда к точке, где определяется напряженность, если заряд положительный (рис. 2, а),



Рисунок 2, а

и в противоположную сторону, если заряд отрицательный (рис. 2, б).



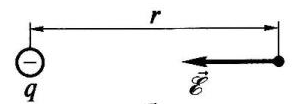
Рисунок 2, б
Если зарядов, создающих электрическое поле, несколько, то напряженность в любой точке поля равна геометрической сумме напряженностей от каждого из них в отдельности. (напряженность электростатического поля нескольких зарядов).

Самостоятельная работа №2

Тема 1.2 Электрические цепи постоянного тока

Электрические цепи постоянного тока – цепи, в которых протекает электрический ток, не изменяющийся во времени ни по величине, ни по направлению. В электрических цепях действуют следующие основные законы: закон Ома и I и II законы Кирхгофа

1. 
   Закон Ома.
   

а) Закон Ома для участка цепи без источника. Сила тока на участке электрической цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка (рис. 1):

---

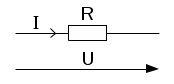
Рис. 1
б) Обобщенный закон Ома (для участка цепи с ЭДС) (рис. 2):

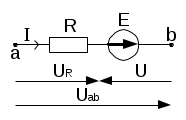а)	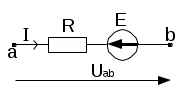б)
Рис. 2

Если направление тока в ветви совпадает с направлением ЭДС источника (рис. 4а), то

.

Если направление тока в ветви не совпадает с направлением ЭДС источника (рис. 4б), то .

2. 
   Законы Кирхгофа (рис. 3).
   

а
) I закон Кирхгофа: алгебраическая сумма токов в узле электрической цепи равна нулю, при этом токи, одинаково направленные относительно узла, записываются с одинаковым знаком.

Для узла а: .

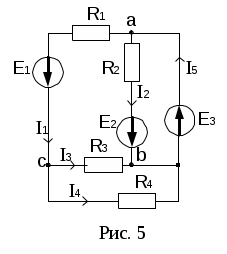
б) II закон Кирхгофа: алгебраическая сумма падений напряжений любого контура равна алгебраической сумме ЭДС этого контура.

Правило знаков: падения напряжения записываются со знаком «+», если направления тока совпадает с направлением обхода контура; ЭДС записываются со знаком «+», если направления ЭДС и обхода контура совпадают.

Рассмотрим схему электрической цепи, приведенную на рис. 3. Направление обхода контура abca выберем по часовой стрелке. Тогда уравнение II закона Кирхгофа будет иметь следующий вид:

.

3. 
   Баланс мощности.
   

Мощность характеризует интенсивность преобразования энергии одного вида в другой за единицу времени.

Для цепи постоянного тока мощность источника: а приемника -

---

, ( =Вт). На основании закона сохранения энергии мощность, развиваемая источниками электроэнергии, должна быть равна сумме мощностей всех приемников и потерь в источниках из-за внутренних сопротивлений. При этом: если направление ЭДС и тока совпадают, то EI в сумме записываются со знаком «+». Для схемы рис. 5 при выбранных направлениях токов:

.

Самостоятельная работа №3

Тема 2.2 Правила Кирхгофа. Расчет сложных электрических цепей

Чтобы расчеты сложных электрических цепей с неоднородными участками не вызывали трудности, существует упрощение с помощью применения правил Кирхгофа, которые рассматривают как обобщение закона Ома на случай разветвленных цепей.

В таких цепях выделяют узловые точки, называемые узлами, где сходятся не менее трех проводников, как изображено на рисунке 1. Токи, поступающие в узел, считают положительными, а вытекающие – отрицательными.



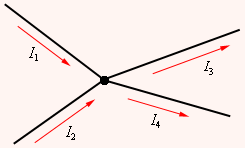
Рисунок 1. Узел электрической цепи. I1, I2>0; I3, I4<0I1, I2>0; I3, I4<0.

В узлах цепи с постоянным током не происходит накопление зарядов. Получаем первое правило (закон) Кирхгофа:

Алгебраическая сумма сил токов для каждого узла разветвленной цепи равняется нулю:

I1+I2+I3+...+In=0I1+I2+I3+...+In=0.

Наличие разветвленной цепи позволяет выделить несколько замкнутых путей, которые состоят из однородных и неоднородных участков. Их принято называть контурами.

На участках с выделенным контуром могут протекать различные токи. Рисунок 2 наглядно показывает пример такой цепи, соответствующей 11 закону Кирхгофа. Она состоит из двух узлов aa и dd, в которых сходятся одинаковые токи. Только один из заданных узлов будет независимым.



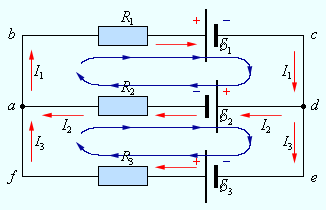
Рисунок 2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (aa или dd) и два независимых контура (например, abcd и adef)

В предложенной цепи выделяют три контура вида abcd, adef и abcdef. Независимыми считаются только два: abcd и adef. Последний из вышеперечисленных не имеет никаких новых участков.

---

Второе правило Кирхгофа – это следствие обобщенного закона Ома.

Для записи обобщенного закона Ома участков, составляющих один из контуров цепи, используется пример, изображенный на рисунке 2 для abcd. Каждому участку задаются положительные направления тока и обхода контура. Для записи следует учитывать «правила знаков», приведенные на рисунке 3.



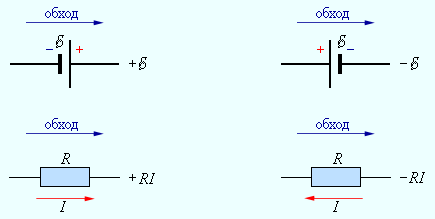
Рисунок 3. «Правила знаков»

Запись обобщенного закона Ома для участков контура abcdabcd принимает вид:

Для bcbc: I1R1=Δφbc−δ1I1R1=∆φbc-δ1.

Для dada: I2R2=Δφda−δ2I2R2=∆φda-δ2.

Сумма левых и правых частей равенств с условием Δφbc=−Δφda∆φbc=-∆φda преобразует выражение:

I1R1+I2R2=Δφbc+Δφda−δ1+δ2=−δ1−δ2I1R1+I2R2=∆φbc+∆φda-δ1+δ2=-δ1-δ2.

Таким же образом можно записать для adefadef контура:

−I2R2+I3R3=δ2+δ3-I2R2+I3R3=δ2+δ3.

2 правило или закон Кирхгофа: алгебраическая сумма сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока этого участка равняется сумме ЭДС вдоль этого контура.

Оба правила Кирхгофа для всех узлов и контуров разветвленной цепи дают необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов электрической цепи. Цепь, изображенная на рисунке 2, рассматривается как система уравнений для определения трех неизвестных I1, I2I1, I2 и I3I3:

I1R1+I2R2=−δ1−δ2I1R1+I2R2=-δ1-δ2,

−I2R2+I3R3=δ2+δ3-I2R2+I3R3=δ2+δ3,

−I1+I2+I3=0-I1+I2+I3=0.

То есть применение этих правил помогает свести расчет электрической цепи постоянного тока к решению системы. Процесс не вызывает трудностей, но зачастую приходится работать с громоздкими выражениями простых цепей. При получении отрицательного значения силы тока на участке цепи говорят о противоположном направлении тока, относительно выбранного.

Самостоятельная работа №4

Тема 2.3 Однофазные электрические цепи синусоидального напряжения

Электрическая цепь синусоидального тока содержит помимо электротехнических устройств, назначение которых совпадает с назначением функционально аналогичных устройств цепи постоянного тока (источники энергии, измерительные приборы, коммутационные аппараты и т.д.), также устройства, присущие только цепям синусоидального тока: трансформаторы, конденсаторы, катушки индуктивности и др.

---

Смотрите также файлы

• Амангелді кімдігіні білім беру блімі А. Нрманов атындаы жалпы білім беретін мектебі кмм.docx

• Бланк сериялы нмірсіз жарамсыз болып табылады. Жауап айтаранда міндетті трде бізді жне кні крсетілуі керек.docx

• азастан Республикасы Оуаарту министріні.docx

• Корреляционный анализ.docx

• 7сынып. Блім Жеіс кні. лы ерлікке тазым. 1нса.docx