Файл: Курсовая работа по дисциплине Информационные технологии.docx

Рисунок 6 - Фрагмент листа MS Excel для экспоненциальной аппроксимации.

Таким образом, уравнение экспоненциальной регрессии имеет вид:

y = 0,001e^0,0132x (25)

2. Представление результатов в виде графиков

Построение линии тренда

Методика проведения данных работ подробно изложена в работе [2]. Результаты представлены на рис. 7-9.



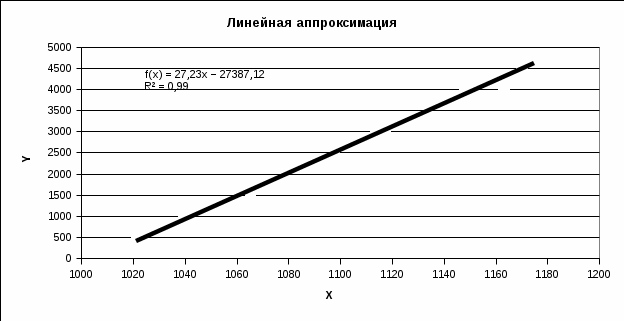
Рисунок 7 - Исходные точки и линия тренда для линейной аппроксимации.



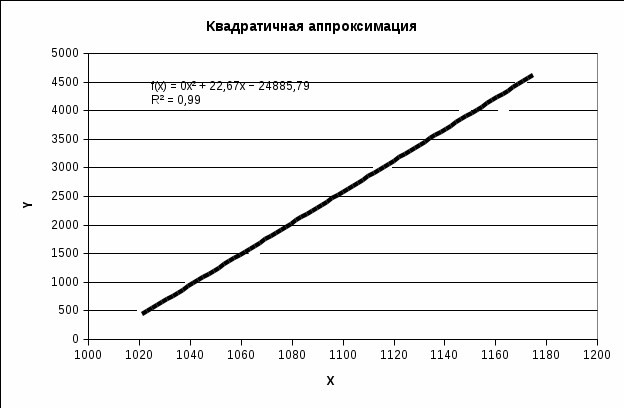
Рисунок 8 -. Исходные точки и линия тренда для квадратичной аппроксимации.



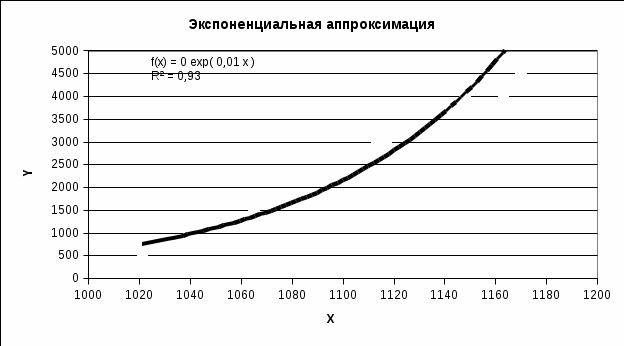
Рисунок 9 - Исходные точки и линия тренда для экспоненциальной аппроксимации.

Сравнивая данные результаты с результатами, полученными вручную ранее с использованием основных расчётных формул, видим, что они полностью совпадают. Это указывает на то, что вычисления верны.

3. Получения числовых характеристик с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ

Методика этих функции подробно изложена в работе [2]. Результаты расчётов представлены на рис. 10-12.

ЛИНЕЙН
27,2338	-27387,1153
0,4853	538,1744
0,9927	111,2072
3149,1371	23
38945535,6098	284442,1500

Рисунок 10 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН

для линейной аппроксимации

ЛИНЕЙН
0,0021	22,672	-24885,789
0,0117	25,815	14163,910
0,9928	113,626	#Н/Д
1508,263	22	#Н/Д
38945938,869	284038,890	#Н/Д

---

Рисунок 11 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН

Для квадратичной аппроксимации

ЛГРФПРИБЛ
1,01332	0,00102
0,00077	0,85066
0,9283	0,175778164
297,72435	23
9,19908	0,71065

Рисунок 12 -. Фрагмент рабочего стола MS Excel использование функции ЛГРФПРИБЛ

для экспоненциальной аппроксимации

Сравнивая результаты, полученные с помощью функции ЛИНЕЙН и ЛГРФПРИБЛ, с результатами полученными вручную с использованием основных расчётов формул, можно видеть , что они полностью совпадают. Это указывает на то, что вычисления верны.

Лучше всего результаты испытаний, аппроксимирует квадратичная функция (24): y = 0,0021x² + 22,672x - 24886 т.к коэффициент детерминировнности квадратичной аппроксимации выше и равен R² = 0,993. Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.

4. Аппроксимация с помощью MathCAD

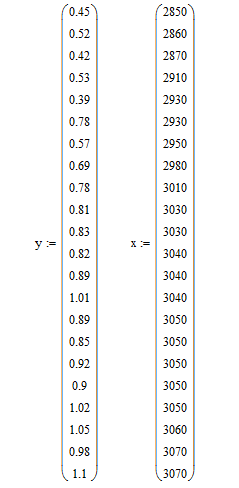
Вводим исходные данные(рис.13)



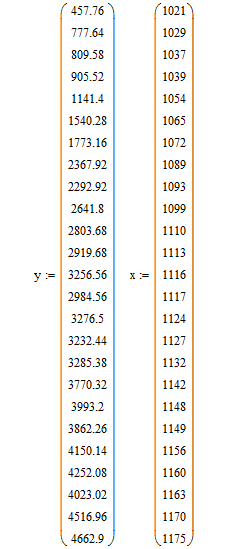
Рисунок 13 - Фрагмент листа MathCAD с исходными данными

Линейная регрессия

Линейная регрессия в системе MathCAD выполняется по векторам аргумента Х и отсчетов Y функциями: intercept(X,Y) – вычисляет параметр a1 , смещение линии регрессии по вертикали; slope(X,Y) – вычисляет параметр a2 , угловой коэффициент линии регрессии. Полученные значения коэффициентов используем в уравнении регрессии

Функция corr(Y,y(x)) - вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости.

Вычислив параметры линейной регрессии, строим графики исходной функции y и функции линейной регрессии f(x)

---

Рисунок 14 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для линейной аппроксимации

Полиномиальная регрессия

Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функцией regress(X,Y,n), которая вычисляет вектор S, в составе которого находятся коэффициенты ai полинома n-й степени. Значения коэффициентов ai могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0). Полученные значения коэффициентов используем в уравнении регрессии/ Вычислив параметры квадратичной регрессии, строим графики исходной функции y и функции квадратичной регрессии f(x)



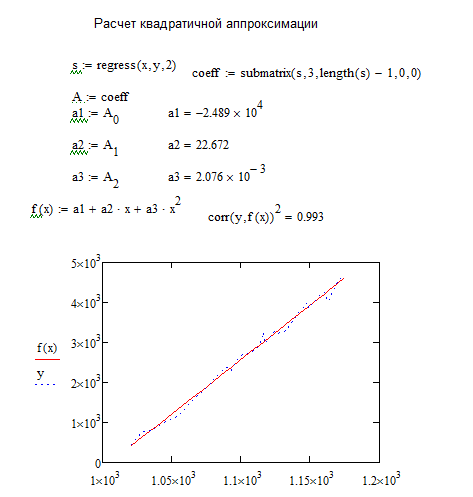
Рисунок 15 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для квадратичной аппроксимации



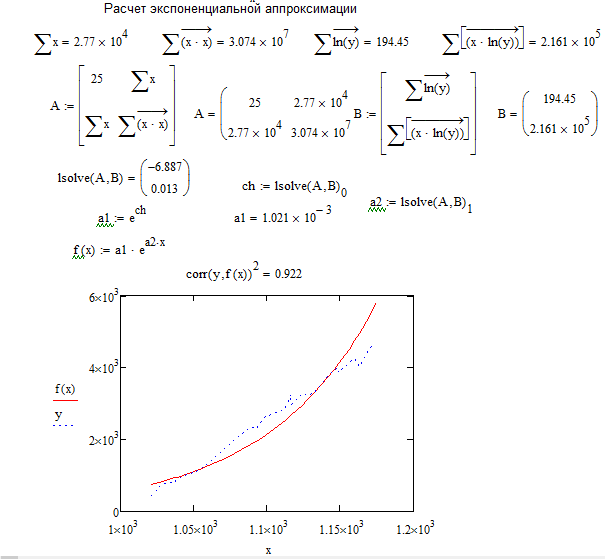
Рисунок 16 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для экспоненциальной аппроксимации

Проведенные расчеты показывают, что результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel.

5. Аппроксимация с помощью VBA

Результат работы программы представлен на рисунках 17-19





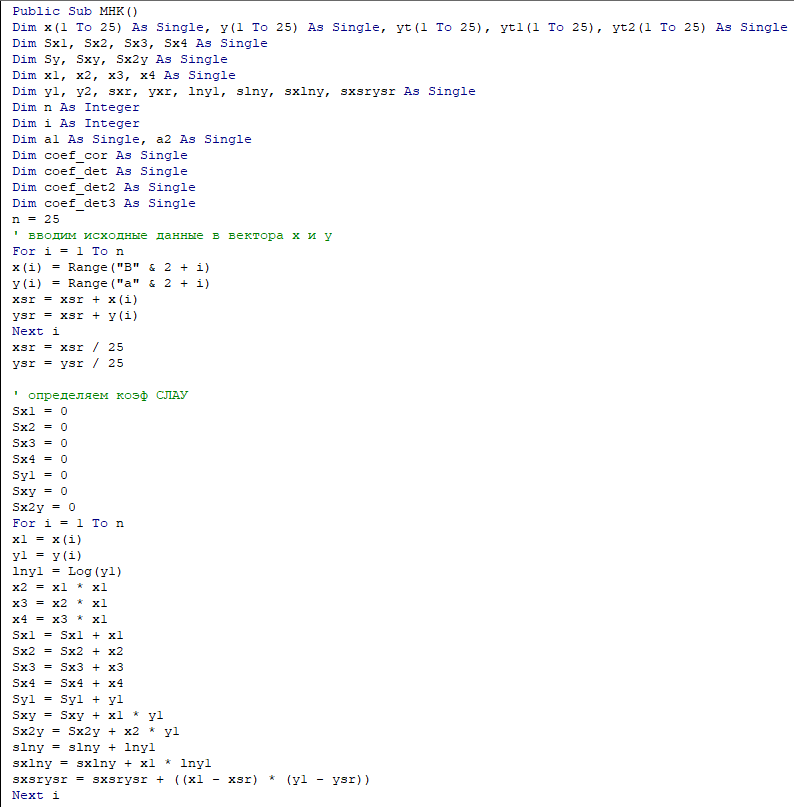
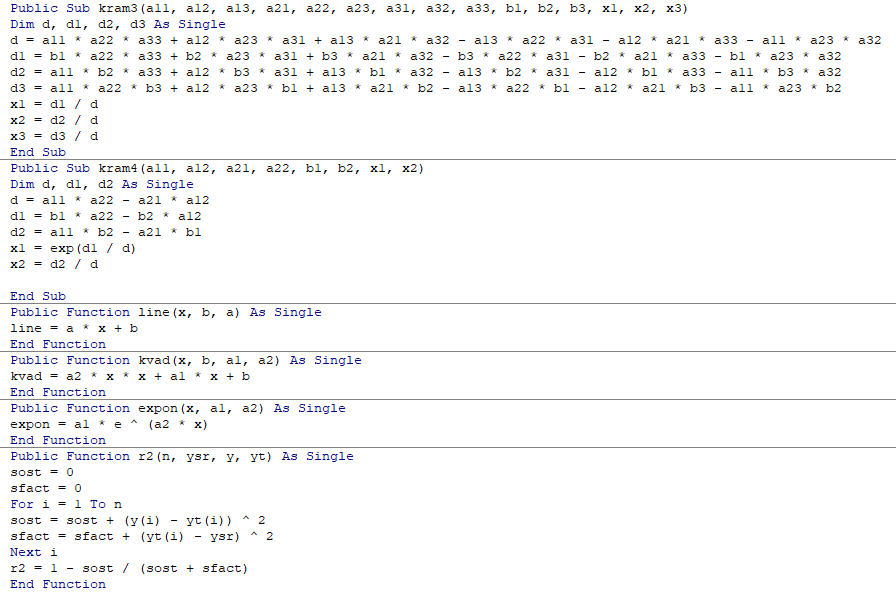
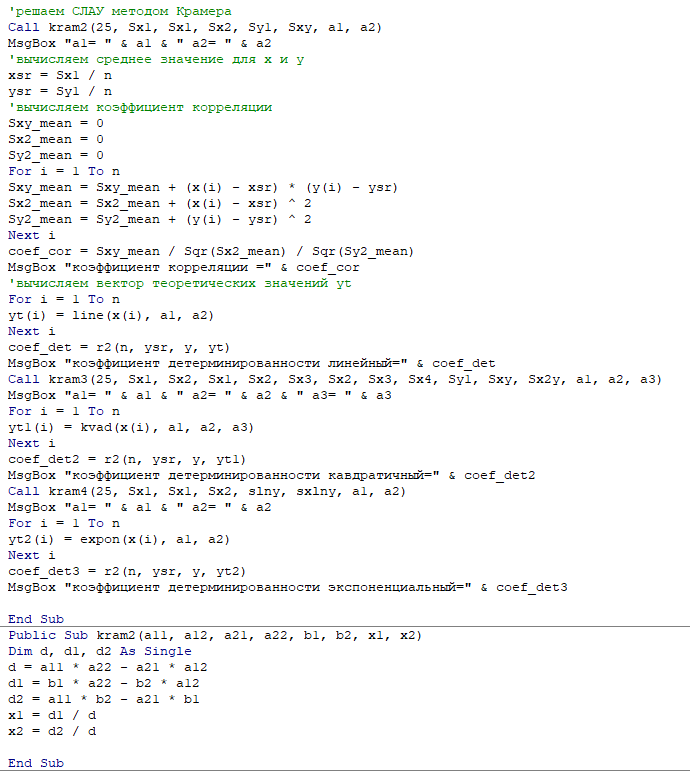
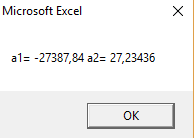
Рисунок 17 – Результат работы программы (Линейная аппроксимация)



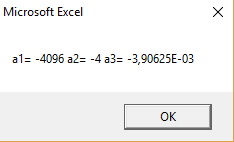
Рисунок 18 – Результат работы программы (Квадратичная аппроксимация)



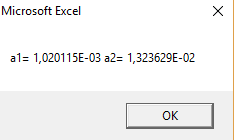
Рисунок 19 – Результат работы программы (Экспоненциальная аппроксимация)

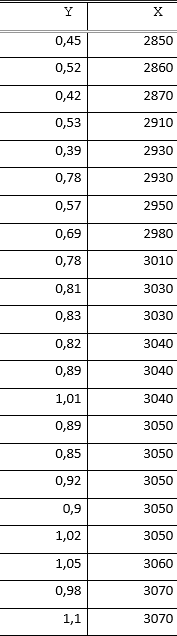
1. Задача 3

---

1. Таблицы, выполненные средствами Microsoft Excel.

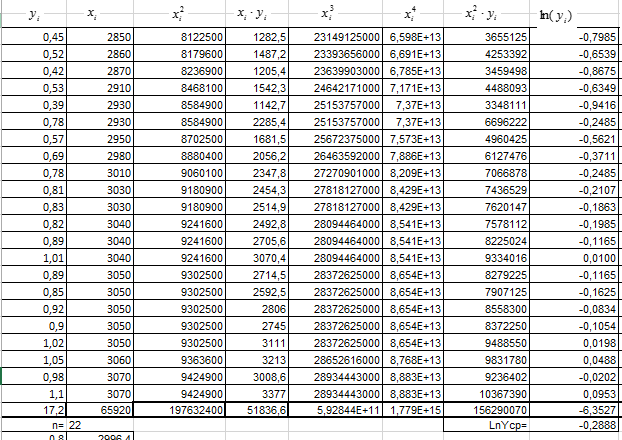
Рисунок 38 вычисления вспомогательных сумм и средних значений.



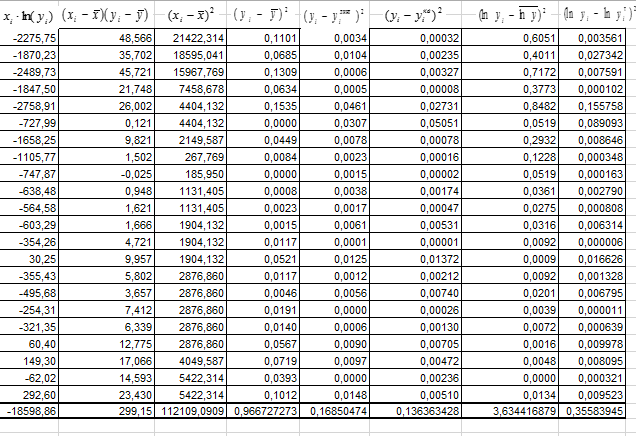
Рисунок 39 - Вычисления вспомогательных сумм (продолжения).

На рис. 40 представлены расчёты для линейной аппроксимации.



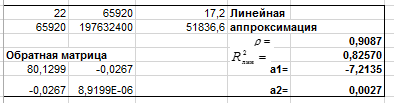
Рисунок 40 - Фрагмент рабочего листа MS Excel для линейной аппроксимации.

Таким образом уравнение линейной регрессии имеет вид:

y = 0,0027x - 7,2135

На рис. 41 представлены расчёты для квадратичной аппроксимации.



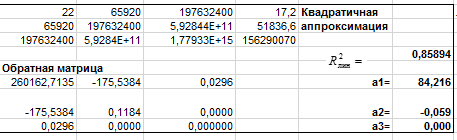
Рисунок 41 Фрагмент рабочего листа MS Excel для квадратичной аппроксимации

Таким образом, уравнение квадратичной регрессии имеет вид:

y = 1E-05x² - 0,059x + 84,216

На рис. 42 представлены расчёты для экспоненциальной аппроксимации.



Рисунок 42 - Фрагмент листа MS Excel для экспоненциальной аппроксимации.

Таким образом, уравнение экспоненциальной регрессии имеет вид:

y = 6E-06e^0,0039x

2. Представление результатов в виде графиков

Построение линии тренда

Методика проведения данных работ подробно изложена в работе [2]. Результаты представлены на рис.



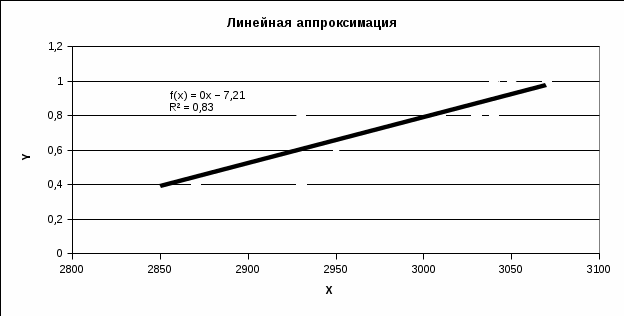
Рисунок 43 - Исходные точки и линия тренда для линейной аппроксимации.



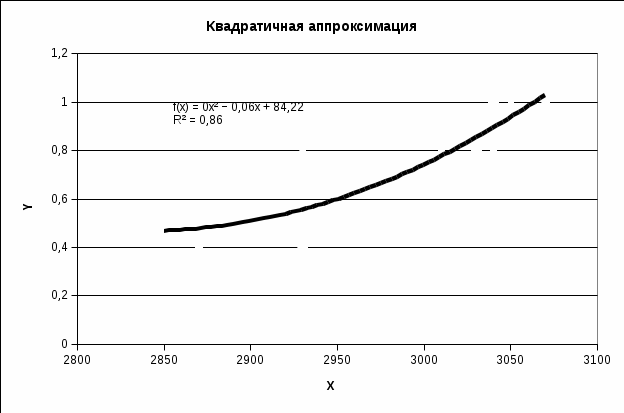
Рисунок 44 -. Исходные точки и линия тренда для квадратичной аппроксимации.



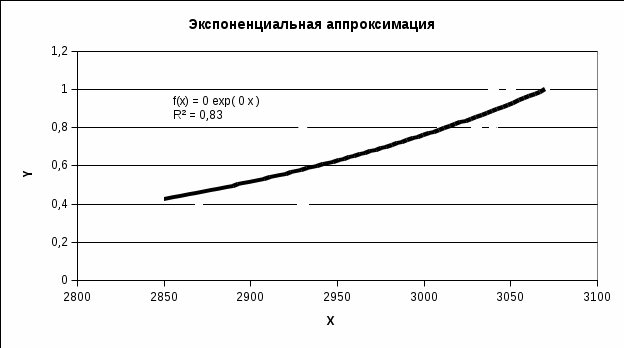
Рисунок 45 - Исходные точки и линия тренда для экспоненциальной аппроксимации.

Сравнивая данные результаты с результатами, полученными вручную ранее с использованием основных расчётных формул, видим, что они полностью совпадают. Это указывает на то, что вычисления верны.

3. Получения числовых характеристик с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ

Результаты расчётов представлены на рис.

ЛИНЕЙН
0,0027	-7,2135
0,0003	0,8217
0,8257	0,0918
94,7419	20
0,7982	0,1685

---

Рисунок 46 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН

для линейной аппроксимации

ЛИНЕЙН
0,0000	-0,059	84,216
0,0000	0,029	43,211
0,8589	0,085	#Н/Д
57,849	19	#Н/Д
0,830	0,136	#Н/Д

Рисунок 47 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН

Для квадратичной аппроксимации

ЛГРФПРИБЛ
1,00390	0,00001
0,00040	1,19401
0,8266	0,133386554
95,37291	20
1,69687	0,35584

Рисунок 48 -. Фрагмент рабочего стола MS Excel использование функции ЛГРФПРИБЛ

для экспоненциальной аппроксимации

Сравнивая результаты, полученные с помощью функции ЛИНЕЙН и ЛГРФПРИБЛ, с результатами полученными вручную с использованием основных расчётов формул, можно видеть , что они полностью совпадают. Это указывает на то, что вычисления верны.

Лучше всего результаты испытаний, аппроксимирует квадратичная функция: y = 1E-05x² - 0,059x + 84,216 т.к коэффициент детерминировнности квадратичной аппроксимации выше и равен R² = 0,859. Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.

4. Аппроксимация с помощью MathCAD

Вводим исходные данные(рис.49)

---