Файл: Курсовая работа по дисциплине Информационные технологии.docx

Рисунок 49 - Фрагмент листа MathCAD с исходными данными

Линейная регрессия

Линейная регрессия в системе MathCAD выполняется по векторам аргумента Х и отсчетов Y функциями: intercept(X,Y) – вычисляет параметр a1 , смещение линии регрессии по вертикали; slope(X,Y) – вычисляет параметр a2 , угловой коэффициент линии регрессии. Полученные значения коэффициентов используем в уравнении регрессии

Функция corr(Y,y(x)) - вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости.

Вычислив параметры линейной регрессии, строим графики исходной функции y и функции линейной регрессии f(x)



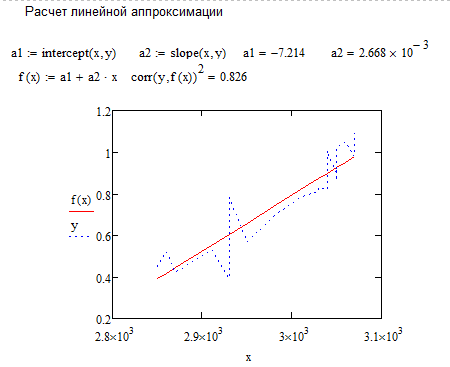
Рисунок 50 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для линейной аппроксимации

Полиномиальная регрессия

Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функцией regress(X,Y,n), которая вычисляет вектор S, в составе которого находятся коэффициенты ai полинома n-й степени. Значения коэффициентов ai могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0). Полученные значения коэффициентов используем в уравнении регрессии/ Вычислив параметры квадратичной регрессии, строим графики исходной функции y и функции квадратичной регрессии f(x)



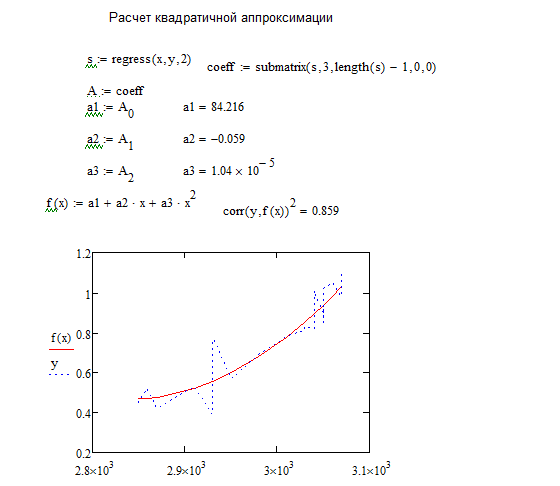
Рисунок 51 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для квадратичной аппроксимации



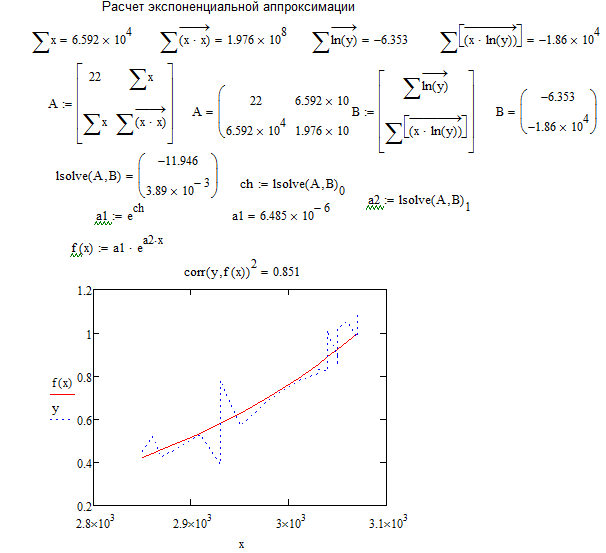
Рисунок 52 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для экспоненциальной аппроксимации

Проведенные расчеты показывают, что результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel.

5. Аппроксимация с помощью VBA

Код программы:

---

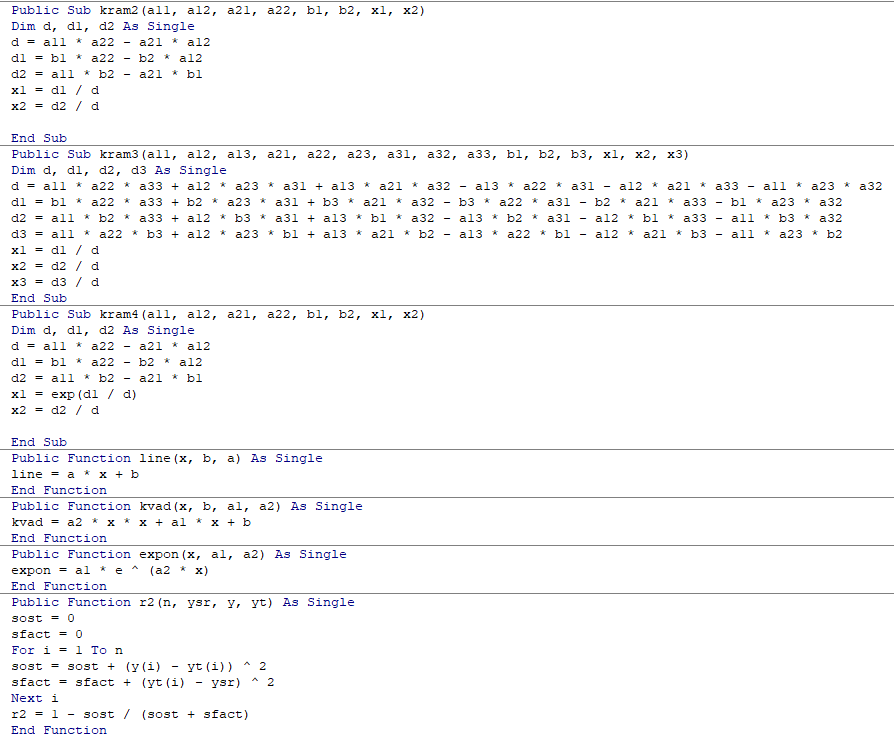
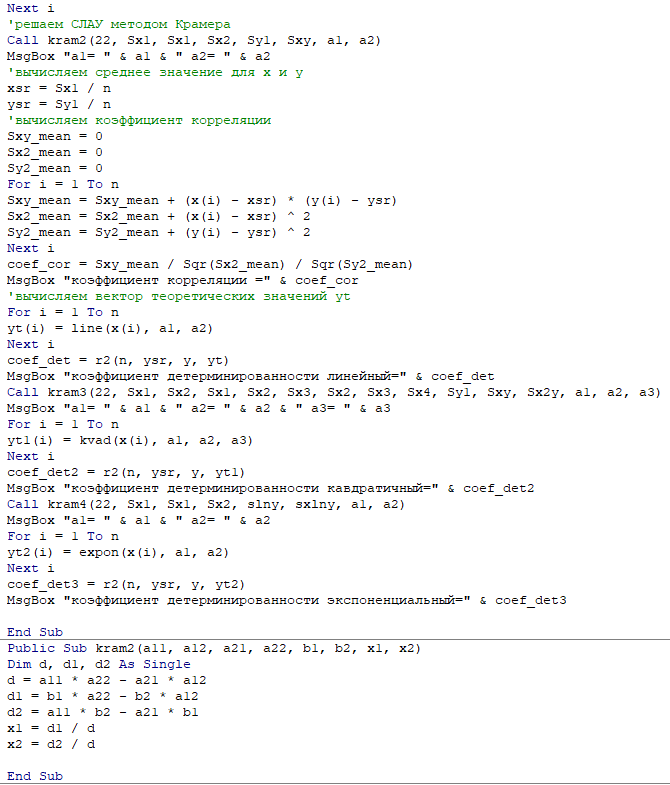
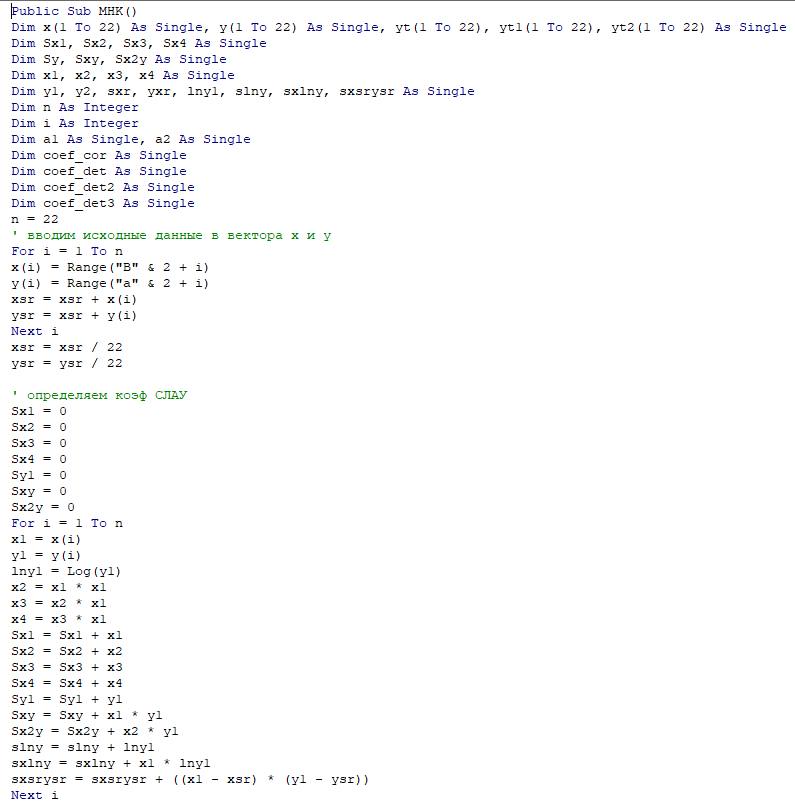
Результат работы программы представлен на рисунках



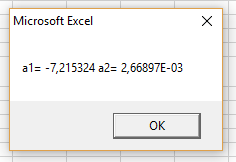
Рисунок 53 – Результат работы программы (Линейная аппроксимация)



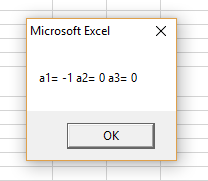
Рисунок 54 – Результат работы программы (Квадратичная аппроксимация)



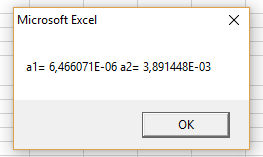
Рисунок 55 – Результат работы программы (Экспоненциальная аппроксимация)

Заключение

Проанализировав результаты решения в различных средах, можно сделать вывод о наличии своих плюсов и минусов работы в каждой из них. Однако незначительные различия в преобразовании численных результатов и обширные возможности экспорта и импорта данных позволяют утверждать, что искажения фактических результатов не происходит.

В ходе выполнения данной работы были получены более глубокие знания и ряд новых навыков в области взаимодействия со средами Microsoft Excel, Mathcad и VBA.

Таким образом цель работы можно считать достигнутой.

Список литературы

1. Воробьева Ф.И. Информатика. MS Excel 2010: учебное пособие / Ф.И. Воробьева, Е.С. Воробьев. Казань. КНИТУ. 2014. 100 с. http://biblioclub.ru/index.php?page=book&id=428798 (Дата обращения 06.09.2019).

2. Грошев А.С. Информатика: учебник для вузов / А.С. Грошев. - Москва; Берлин: Директ-Медиа. 2015. 484 с. http://biblioclub.ru/index.php?page=book&id=428591 (Дата обращения 06.09.2019). / А.С. Грошев. - 2-е изд. - Москва; Берлин: Директ-Медиа. 2015. 285 с. http://biblioclub.ru/index.php?page=book&id=434666 (Дата обращения 06.09.2019).

4. Агафонов Е.Д. Прикладное программирование: учебное пособие / Е.Д. Агафонов, Г.В. Ващенко. Красноярск: Сибирский федеральный университет. 2015. 112 с. http://biblioclub.ru/index.php?page=book&id=43564 (Дата обращения 06.09.2019).

5.Методические указания по выполнению курсовой работы для студентов специальности 130403. /Беляев В.В., Саттарова Н. И. – СПб.: РИЦ горн. ин-т., 2010

6.Правила оформления курсовых и квалификационных работ. Методические указания. /Онушкина И.О., Талалай П. Г. – СПб.: РИЦ горн. ин-т., 2005

---