Файл: Расчетнографическое задание 2.docx

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждениевысшего образованияСанкт-Петербургский горный университетКафедра строительства горных предприятий и подземных сооруженийРасчетно-графическое задание 2По дисциплине Механика сплошной среды ^{(наименование учебной дисциплины согласно учебному плану)}Тема работы: Расчет параметров напряженно-деформированного состояния массива горных пород в окрестности горной выработки кругового очертанияВыполнил: студент гр. НГШ-20 Коваленко А.Р. ^{(шифр группы) (подпись) (Ф.И.О.)}Оценка:Дата:Проверил: Ассистент Иовлев Г. А. ^{(должность) (подпись) (Ф.И.О.)}Санкт-Петербург2022

Цель работы.

Рассчитать величины и оценить закономерности распределения компонент напряжений и смещений в окрестности незакрепленной горной выработки кругового очертания, расположенной в изотропном линейно-упругом массиве.

Исходные данные.

Рассчитать компоненты напряжений σ_R, σ_θ, σ_z и τ_Rθ в изотропном упругом массиве пород на контуре и в окрестности незакрепленной выработки кругового очертания при коэффициентах бокового распора λ=1 и λ=λ₂. Для этих же условий рассчитать величины смешений контура выработки u_r и u_θ.Для построения эпюр при λ=λ₂ рассмотреть направления с угловой координатой θ=0, 45 и 90⁰. Безразмерный радиус r=R/R₀ (R – текущий радиус; R₀ – радиус выработки) принимать в диапазоне от 1 до 12 (не менее 10 точек).

№ варианта	Глубина заложения выработки H, м	Удельный вес пород γ, МН/м3	Е, МПа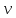
6	495	0,026	8000	0,25

---

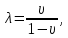
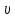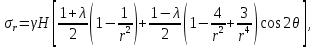
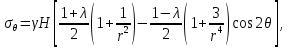
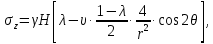
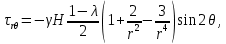
Таблица 1В рамках данного расчетно-графического задания предполагается использование линейно-упругой модели массива пород. Для этой модели коэффициент бокового распора следует определять согласно гипотезе Динника:где – коэффициент Пуассона массива горных пород.Для определения компонент напряженного состояния в окрестности горной выработки воспользуемся решением задачи Кирша из теории упругости:где 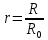– приведенное расстояние до рассматриваемой точки массива в окрестности горной выработки; 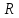- расстояние до рассматриваемой точки массива в окрестности горной выработки; 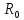– радиус горной выработки; 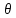– угловая координата (см. рисунок 2).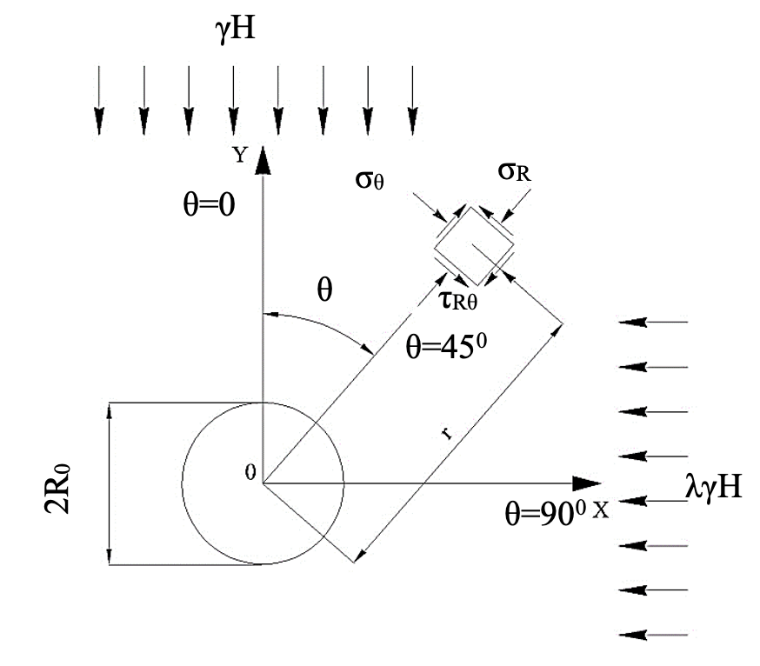Рисунок 1 – Расчетная схема к задаче КиршаДля построения эпюры распределения нормальных тангенциальных напряжений на контуре выработки необходимо задать приведенное расстояние до рассматриваемой точки массива в окрестности горной выработки равным 1 и преобразовать соответствующую формулу решения Кирша в следующий вид: 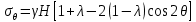.Смещения точек массива в окрестности горной выработки следует определять по следующим формулам: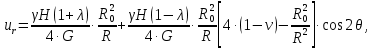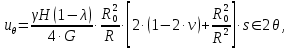где 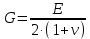– модуль сдвига массива горных пород в окрестности горной выработки;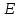

---

– модуль деформации массива горных пород в окрестности горной выработки.

Для построения эпюры распределения смещений на контуре выработки следует подставить в вышеприведенные формулы смещений .

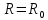Последовательность выполнения расчетно-графической работы.

1. Выполняется построение эпюр распределения ненулевых компонент напряжений для случая λ=1.2. Выполняется построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ=1.3. Выполняется построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ=1.4. Выполняется построение эпюр распределения ненулевых компонент напряжений для направлений с угловой координатой θ=0, 45 и 90⁰ для случая λ= λ₂.5. Выполняется построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ= λ₂.6. Выполняется построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ= λ₂.1. 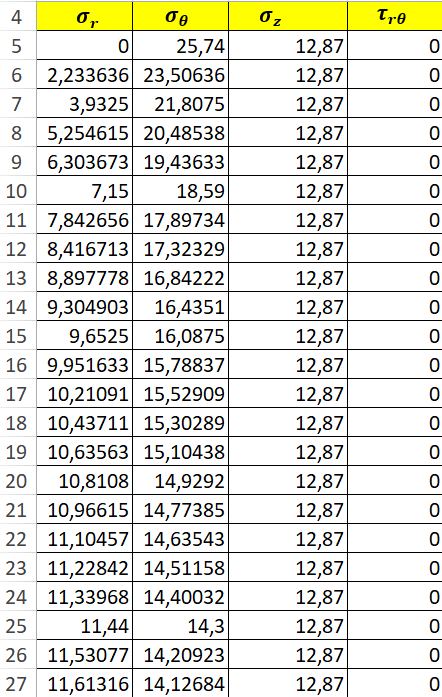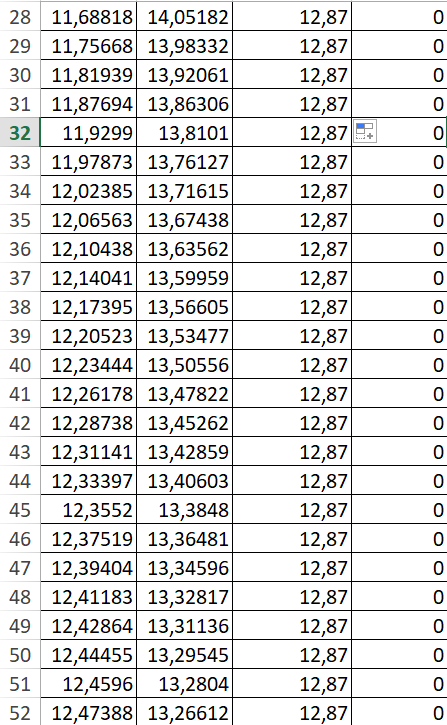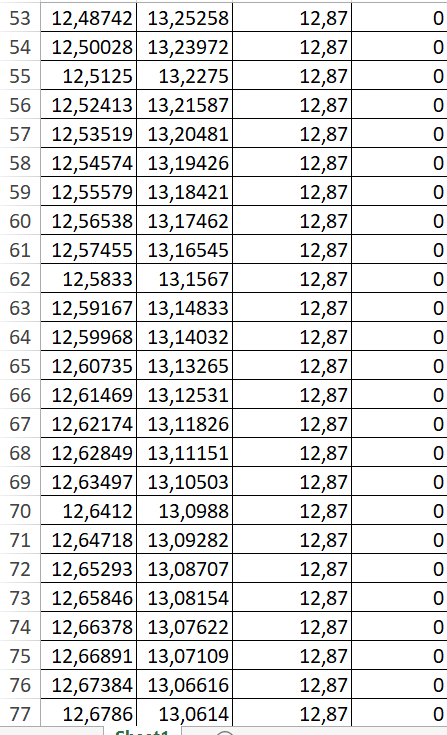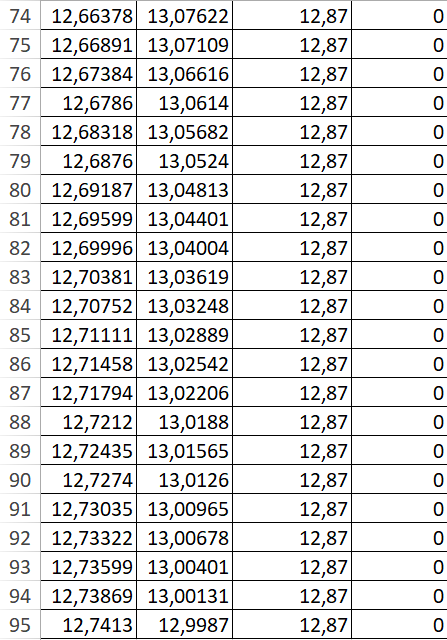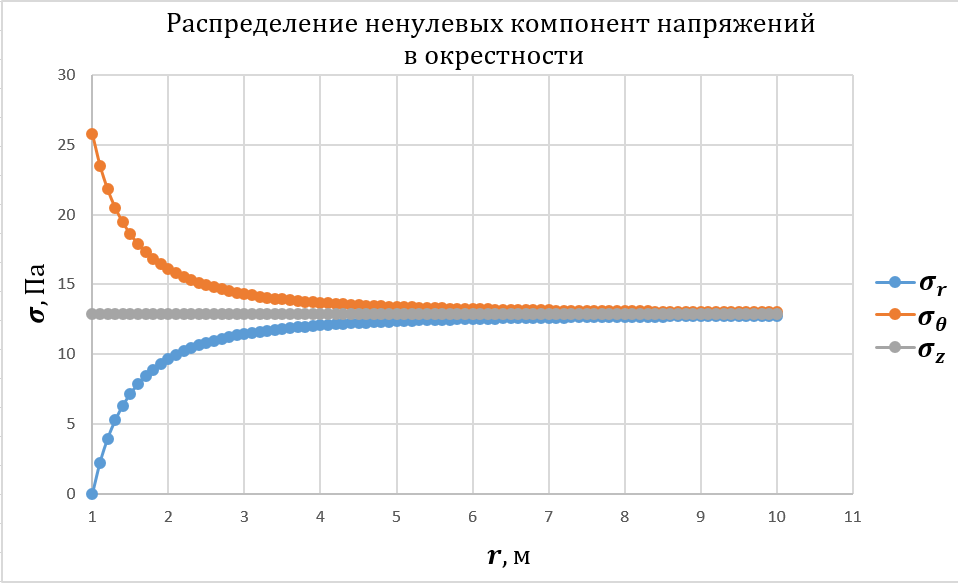Выполняется построение эпюр распределения ненулевых компонент напряжений для случая λ=1.Таблица 2 Рисунок 2

---

.
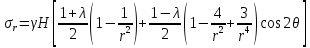
2. Выполняется построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ=1.



Таблица 3



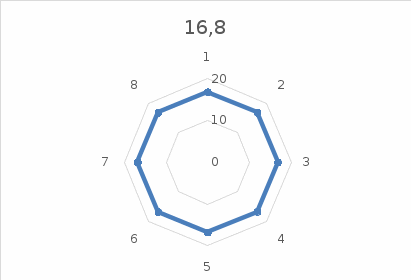
Рисунок 3
3. Выполняется построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ=1.



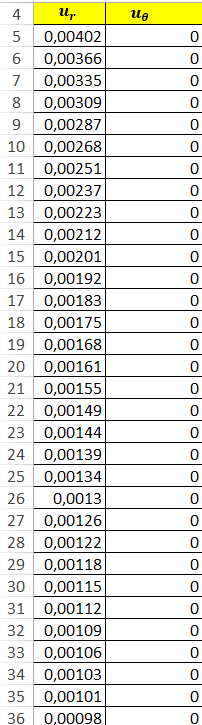
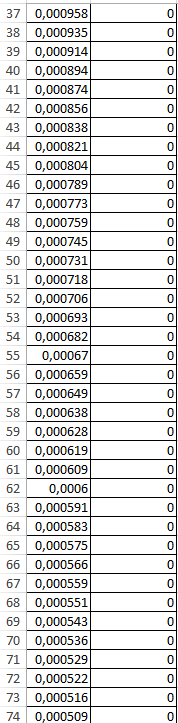
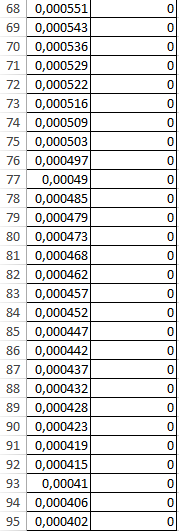
Таблица 4


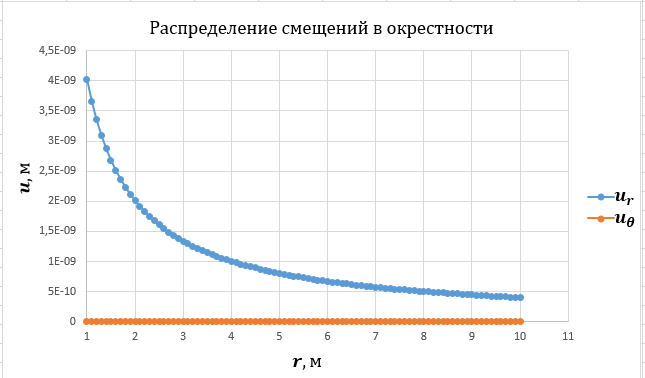
Рисунок 4
4. Выполняется построение эпюр распределения ненулевых компонент напряжений для направлений с угловой координатой θ=0, 45 и 90⁰ для случая λ= λ₂.



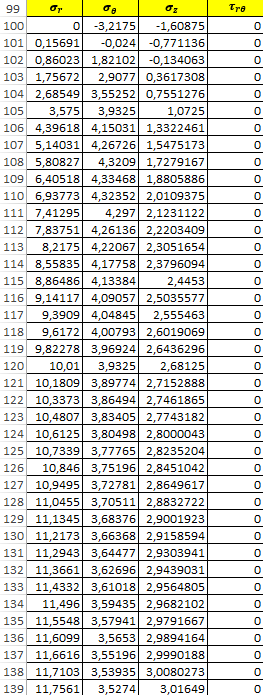
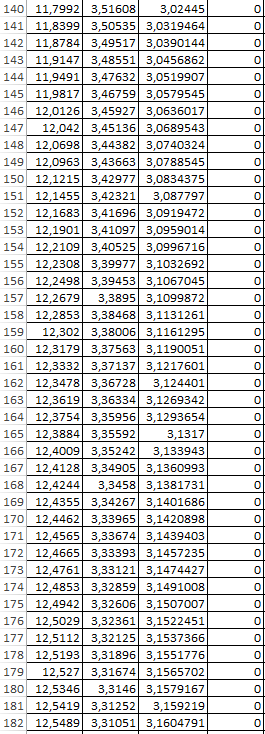
Таблица 5




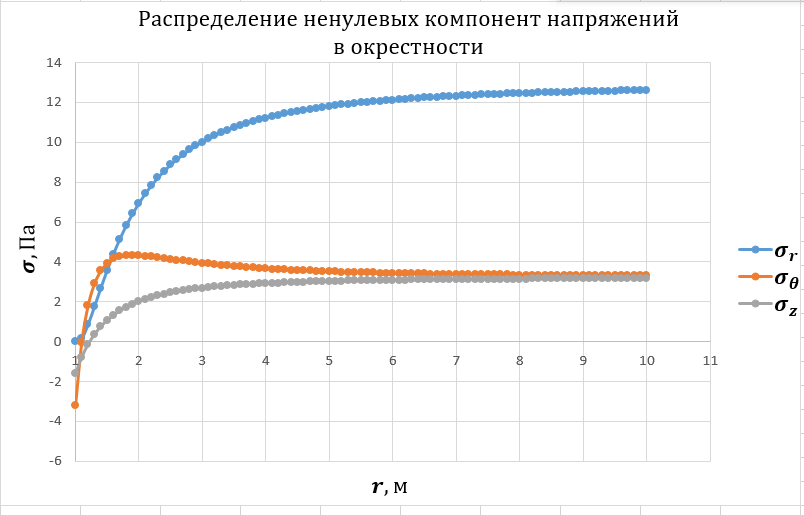
Рисунок 5


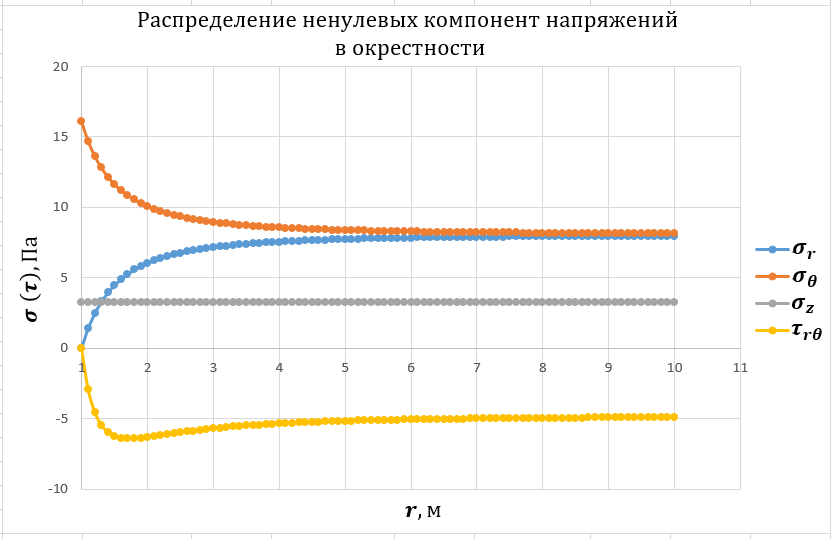
Рисунок 6



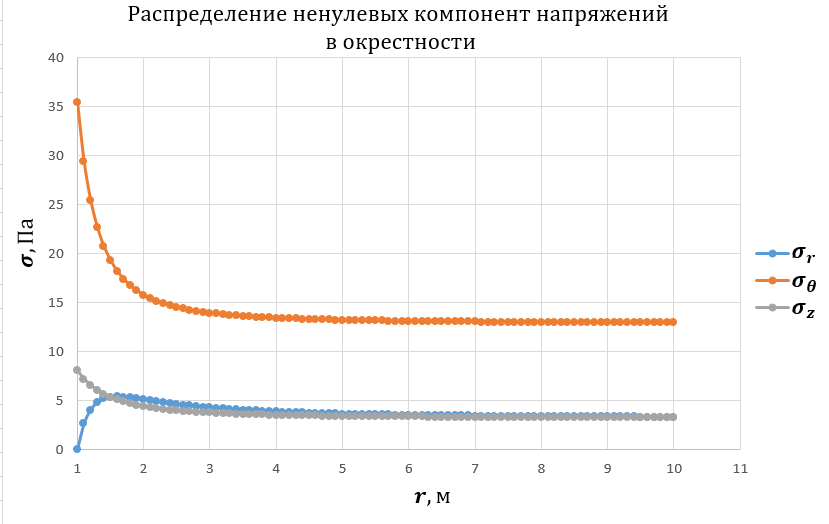
Рисунок 7

5. Выполняется построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ= λ2.

---

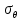-2,86E-15
5,0260476
17,16
29,293952
34,32
29,293952
17,16
5,0260476
-2,86E-15
5,0260476
17,16
29,293952
34,32
29,293952
17,16
5,0260476
-2,86E-15

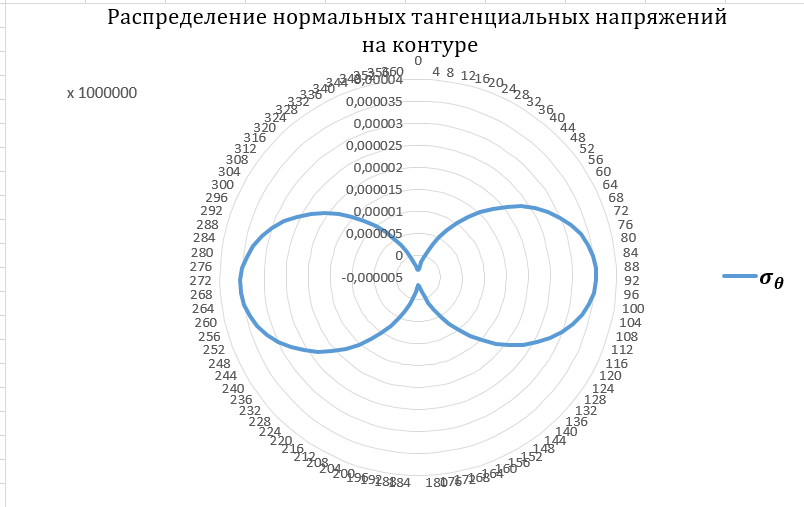
Таблица 5Рисунок 86. Выполняется построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ= λ2.

---

1	0,002514	0
2	0,002438	0,00043
3	0,00222	0,000808
4	0,001885	0,001088
5	0,001475	0,001238
6	0,001039	0,001238
7	0,000628	0,001088
8	0,000294	0,000808
9	7,58E-05	0,00043
10	0	1,54E-19
11	7,58E-05	-0,00043
12	0,000294	-0,00081
13	0,000628	-0,00109
14	0,001039	-0,00124
15	0,001475	-0,00124
16	0,001885	-0,00109
17	0,00222	-0,00081
18	0,002438	-0,00043
19	0,002514	-3,1E-19
20	0,002438	0,00043
21	0,00222	0,000808
22	0,001885	0,001088
23	0,001475	0,001238
24	0,001039	0,001238
25	0,000628	0,001088
26	0,000294	0,000808
27	7,58E-05	0,00043
28	0	4,62E-19
29	7,58E-05	-0,00043
30	0,000294	-0,00081
31	0,000628	-0,00109

---