• 
  владеть основными методами решения задач на смеси, сплавы, концентрации, использовать их в новых ситуациях по отношению к изученным в процессе обучения;
  

• 
  решать задачи на проценты, в том числе, сложные проценты с обоснованием, используя разные способы;
  
• 
  решать логические задачи разными способами, в том числе, с двумя блоками и с тремя блоками данных с помощью таблиц;
  
• 
  решать задачи по комбинаторике и теории вероятностей на основе использования изученных методов и обосновывать решение;
  
• 
  решать несложные задачи по математической статистике;
  
• 
  овладеть основными методами решения сюжетных задач: арифметический, алгебраический, перебор вариантов, геометрический, графический, применять их в новых по сравнению с изученными ситуациях.
  

В повседневной жизни и при изучении других предметов:

• 
  конструировать новые для данной задачи задачные ситуации с учетом реальных характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества; решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;
  
• 
  решать задачи на движение по реке, рассматривая разные системы отсчета;
  
• 
  конструировать задачные ситуации, приближенные к реальной действительности.
  

История математики

• 
  Понимать математику как строго организованную систему научных знаний, в частности владеть представлениями об аксиоматическом построении геометрии и первичными представлениями о неевклидовых геометриях;
  
• 
  рассматривать математику в контексте истории развития цивилизации и истории развития науки, понимать роль математики в развитии России.
  

Методы математики

• 
  Владеть знаниями о различных методах обоснования и опровержения математических утверждений и самостоятельно применять их;
  
• 
  владеть навыками анализа условия задачи и определения подходящих для решения задач изученных методов или их комбинаций;
  
• 
  характеризовать произведения искусства с учетом математических закономерностей в природе, использовать математические закономерности в самостоятельном творчестве.
  

Содержание курса математики в 8-9 классах (углубленный уровень)

Алгебра 8 класс

Числа

---

Рациональные числа

Сравнение рациональных чисел. Действия с рациональными числами. Конечные и бесконечные десятичные дроби. Представление рационального числа в виде десятичной дроби.

Иррациональные числа

Понятие иррационального числа. Распознавание иррациональных чисел. Действия с иррациональными числами. Свойства действий с иррациональными числами. Сравнение иррациональных чисел. Множество действительных чисел.

Представления о расширениях числовых множеств.

Тождественные преобразования

Числовые и буквенные выражения

Преобразования числовых выражений, содержащих степени с целым показателем.

Многочлены

Квадратный трехчлен. Корни квадратного трехчлена. Разложение на множители квадратного трехчлена. Теорема Виета. Теорема, обратная теореме Виета. Выделение полного квадрата. Разложение на множители способом выделения полного квадрата.

Понятие тождества

Представление о тождестве на множестве.

Дробно-рациональные выражения

Алгебраическая дробь. Преобразования выражений, содержащих степени с целым показателем. Допустимые значения переменных в дробно-рациональных выражениях. Сокращение алгебраических дробей. Приведение алгебраических дробей к общему знаменателю. Действия с алгебраическими дробями: сложение, умножение, деление.

Иррациональные выражения

Арифметический квадратный корень. Допустимые значения переменных в выражениях, содержащих арифметические квадратные корни. Преобразование выражений, содержащих квадратные корни.

Уравнения

Представление о равносильности уравнений и уравнениях-следствиях.

Представление о равносильности на множестве. Равносильные преобразования уравнений.

Методы решения уравнений

Методы равносильных преобразований, метод замены переменной, графический метод. Использование свойств функций при решении уравнений, использование теоремы Виета для уравнений степени выше 2.

Квадратное уравнение и его корни

Дискриминант квадратного уравнения. Формула корней квадратного уравнения. Количество действительных корней квадратного уравнения. Решение квадратных уравнений: графический метод решения, использование формулы для нахождения корней, разложение на множители, подбор корней с использованием теоремы Виета. Биквадратные уравнения. Уравнения, сводимые к линейным и квадратным. Квадратное уравнение с параметром. Решение простейших квадратных уравнений с параметрами. Решение некоторых типов уравнений 3 и 4 степени.

---

Дробно-рациональные уравнения

Решение дробно-рациональных уравнений.

Простейшие иррациональные уравнения вида: ; и их решение. Решение иррациональных уравнений вида .

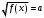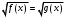
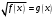Системы уравнений

Уравнение с двумя переменными. Решение уравнений в целых числах. Линейное уравнение с двумя переменными. Графическая интерпретация линейного уравнения с двумя переменными.

Представление о графической интерпретации произвольного уравнения с двумя переменными: линии на плоскости.

Понятие системы уравнений. Решение систем уравнений.

Представление о равносильности систем уравнений.

Методы решения систем линейных уравнений с двумя переменными графический метод, метод сложения, метод подстановки. Количество решений системы линейных уравнений. Система линейных уравнений с параметром.

Системы нелинейных уравнений. Методы решения систем нелинейных уравнений. Метод деления, метод замены переменных. Однородные системы.

Неравенства

Числовые неравенства. Свойства числовых неравенств. Проверка справедливости неравенств при заданных значениях переменных.

Неравенство с переменной. Строгие и нестрогие неравенства. Доказательство неравенств. Неравенства о средних для двух чисел.

Понятие о решении неравенства. Множество решений неравенства.

Представление о равносильности неравенств.

Линейное неравенство и множества его решений. Решение линейных неравенств. Линейное неравенство с параметром.

Системы неравенств

Системы неравенств с одной переменной. Решение систем неравенств с одной переменной: линейных, квадратных, дробно-рациональных, иррациональных. Изображение решения системы неравенств на числовой прямой. Запись решения системы неравенств.

---

Функция

Способы задания функций: аналитический, графический, табличный. График функции. Примеры функций, получаемых в процессе исследования различных процессов и решения задач. Значение функции в точке. Свойства функций: область определения, множество значений, нули, промежутки знакопостоянства, возрастание и убывание, промежутки монотонности, наибольшее и наименьшее значение, периодичность. Исследование функции по ее графику.

Квадратичная функция

Свойства. Парабола. Построение графика квадратичной функции. Положение графика квадратичной функции в зависимости от ее коэффициентов. Использование свойств квадратичной функции для решения задач.

Обратная пропорциональность

Свойства функции . Гипербола. Представление об асимптотах.

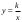
Степенная функция с показателем 3

Свойства. Кубическая парабола.

Функции 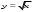, , 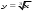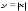.Их свойства и графики. Степенная функция с показателем степени больше 3.

Преобразование графиков функций: параллельный перенос, симметрия, растяжение/сжатие, отражение.

Представление о взаимно обратных функциях.

Непрерывность функции и точки разрыва функций. Кусочно-заданные функции.

Решение текстовых задач

Задачи на все арифметические действия

Решение текстовых задач арифметическим способом. Использование таблиц, схем, чертежей, других средств представления данных при решении задачи.

Решение задач на движение, работу, покупки

Анализ возможных ситуаций взаимного расположения объектов при их движении, соотношения объемов выполняемых работ при совместной работе.

Решение задач на нахождение части числа и числа по его части

---

Решение задач на проценты, доли, применение пропорций при решении задач.

Логические задачи

Решение логических задач. Решение логических задач с помощью графов, таблиц.

Основные методы решения задач

Арифметический, алгебраический, перебор вариантов. Первичные представления о других методах решения задач (геометрические и графические методы).

Статистика и теория вероятностей

Статистика

Диаграммы рассеивания. Описательные статистические показатели: среднее арифметическое, медиана, наибольшее и наименьшее значения числового набора. Отклонение. Случайные выбросы. Меры рассеивания: размах, дисперсия и стандартное отклонение. Свойства среднего арифметического и дисперсии. Случайная изменчивость. Изменчивость при измерениях. Решающие правила. Закономерности в изменчивых величинах.

История математики

Возникновение математики как науки, этапы ее развития. Основные разделы математики. Выдающиеся математики и их вклад в развитие науки.

Бесконечность множества простых чисел. Числа и длины отрезков. Рациональные числа. Потребность в иррациональных числах. Школа Пифагора

Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений степеней, больших четырех. Н. Тарталья, Дж. Кардано, Н.Х. Абель, Э.Галуа.

Появление метода координат, позволяющего переводить геометрические объекты на язык алгебры. Появление графиков функций. Р. Декарт, П. Ферма. Примеры различных координат.

Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске. Сходимость геометрической прогрессии.

---

Смотрите также файлы

• Тема Аналитический метод решения задачи параметрического программирования.doc

• Исследование функций слуха аудиометром как классический скрининг, так и применение современных объективных методов, позволяет своевременно выявить и определить степень тяжести таких заболеваний как кондуктивная тугоухость,.docx

• Сор 6 за тему Сатира и юмор в литературе Д. И. Фонвизин Недоросль.docx

• .docx

• Тербелістер жне толындар Педагогті атыжні.docx