Оптимальное решение по второму критерию (ячейки B4:C4) состоит в выпуске шкафов и столов в количествах 20 и 34 ед., минимальный штраф за простой оборудования (ячейка G10) составляет w_min = 36 ден.ед., При этом прибыль (ячейка D11) равна F = 1614 ден.ед., z = 1650 ден.ед.

Полученные результаты оптимизации по двум критериям сведены в табл. 8.

Таблица 8

Критерий оптимальности	Продукция			Значения целевых функций
	Вершина на рис.1	Шкаф	Стол	z, ден.ед.	w, ден.ед.	F, ден.ед
Прибыль от реализации продукции	C	38	20	2020	134,4	1885,6
Штраф за простой станков	B	20	34	1650	36	1614

На рис. 1 оптимальному плану по прибыли соответствует вершина C(38;20), а оптимальному плану по штрафу – вершина C(20;34).

---

2 ТРАНСПОРТНАЯ ЗАДАЧА

Задание 2

Предположим, что запасы груза в пунктах отправления равны соответственно 290, 150 и 80 единиц. Потребности пунктов назначения составляют соответственно 30, 50, 100, 150, 190 единиц. Затраты на перевозку единицы груза (тарифы) 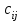содержатся в матрице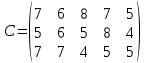



2.1 Таблица перевозок

Имеем транспортную задачу с тремя поставщиками и пятью потребителями, исходные данные которой можно представить в виде табл. 9.

Таблица 9

Пункты отправления и запасы груза		Пункты назначения и потребности
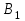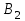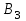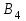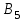		30		50			100			150			190
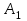	290		7			6			8			7			5
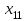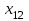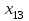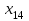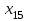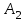	150		5			6			5			8			4
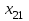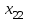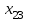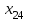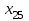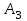	80		7			7			4			5			5

---

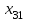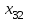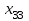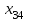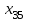2.2 Математическая модель

Определим сначала вид транспортной модели. Для этого вычислим суммарные запасы груза у поставщиков



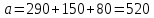
и суммарные потребности



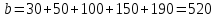
Так как 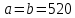, то модель является закрытой, и задача обязательно имеет оптимальное решение.

Суммарные транспортные затраты на перевозки груза от поставщиков к потребителям составляют

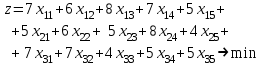. (8)

Ограничения показывают, что все запасы должны быть вывезены от поставщиков

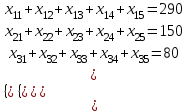(9)

и должны быть удовлетворены потребности пунктов назначения

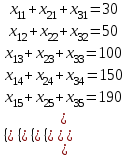. (10)

Все поставки груза должны быть неотрицательными

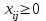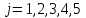, , . (11)

Соотношения (8) – (11) образуют математическую модель транспортной задачи.
2.3 «Равномерный» план перевозок

В среде Excel на листе 1 в блоке ячеек B2:F4 поместим тарифы на перевозки из табл. 9. Блок ячеек B7:F9 предусмотрим для записи плана перевозок. В ячейки H7:H9 запишем запасы груза у поставщиков, а в ячейки B11:F11 – потребности пунктов назначения. Суммарные затраты на перевозку будем рассчитывать в ячейке G2, в которую поместим формулу = СУММПРОИЗВ(B2:F4;B7:F9). Содержимое этой ячейки сначала равно нулю. Однако, постепенно заполняя ячейки B7:F9 числами, содержимое ячейки.

Чтобы получить «равномерный» план перевозок, запасы поставщика А₁ разделим примерно поровну между потребителями (290/5=58 ден. ед.). Так у потребителя В₁ потребность только в 30 д.е., то направляем 30 ден. ед., в В₂ – 50 ден. ед. Тем самым потребитель В₁ и В₂ получит груз в нужном объеме, и тогда поставки от других поставщиков будут нулевыми. Распределяя «равномерно» запасы поставщика А

---

₂ между оставшимися потребителями, видим, что каждому следует направить по 30 ед. груза. Однако, потребителю В₃ достаточно направить лишь 6 ед., что и записывается в соответствующей клетке. Остальной груз в объеме 144 ед. распределяем так, как это показано в табл.10. В строку, соответствующую поставкам А₃, поместим остаточные значения объемов груза.

Таблица 10

	A	B	C	D	E	F	G		H
1		Тарифы на перевозку груза
2		7	6	8	7	5	3196
3		5	6	5	8	4
4		7	7	4	5	5
5		"Равномерный" план перевозок
6		B1	B2	B3	B4	B5			Запасы
7	A1	30	50	94	58	58			290
8	A2	0	0	6	58	86			150
9	A3	0	0	0	34	46			80
10
11	Потребности	30	50	100	150	190

---

После заполнения перевозок в клетке G2 мы автоматически получим суммарные затраты, равные 3196 руб.
2.4 План перевозок, полученный методом «северо-западного» угла

Следующий план перевозок получим в Excel на листе 2. Отличие от предыдущего плана состоит только в заполнении блока ячеек B7:F9. Поэтому можно скопировать лист 1 на лист 2 и изменить только содержимое указанного блока. В ячейку B7 («северо-западная» клетка) поставим максимально допустимую перевозку, равную min(290;30) = 30. Тогда перевозки в пункт от других поставщиков должны быть равны нулю. Первый столбец оказался заполненным. Переходим к заполнению следующей «северо-западной» клетки C7, учитывая, что запас поставщика уменьшился на 30 и стал равен 260 ед. В ячейку C7 поставим перевозку, равную min(260;50) = 50. Тогда перевозки в пункт от других поставщиков должны быть равны нулю. Второй столбец оказался заполненным. Переходим к заполнению следующей «северо-западной» клетки D7, учитывая, что запас поставщика уменьшился еще на 50 и стал равен 210 ед. В ячейку D7 поставим перевозку, равную min(210;100) = 50. Тогда перевозки в пункт от других поставщиков должны быть равны нулю. Третий столбец оказался заполненным. Переходим к заполнению следующей «северо-западной» клетки Е7, учитывая, что запас поставщика уменьшился еще на 100 и стал равен 110 ед. В ячейку Е7 поставим перевозку, равную min(110;110) = 50. Тогда перевозки из пункта остальным потребителям должны быть равны нулю. Первая строка оказалась заполненной. При этом потребность пункта В₄ уменьшилась на величину 110 ед. и стала равной 40 ед. Продолжая этот процесс дальше, получим план перевозок, представленный в табл. 11.

Таблица 11

	A	B	C	D	E	F	G		H
1		Тарифы на перевозку груза
2		7	6	8	7	5	3240
3		5	6	5	8	4
4		7	7	4	5	5
5		План по методу "Северо-западного" угла
6		B1	B2	B3	B4	B5			Запасы
7	A1	30	50	100	110	0			290
8	A2	0	0	0	40	110			150
9	A3	0	0	0	0	80			80
10
11	Потребности	30	50	100	150	190

---

Смотрите также файлы

• Эссе біріай трбиелік ортада трбие жйесін руа байланысты сынып жетекшіні іс рекеті.docx

• Среди причин, вследствие которых началась чеченская война, выделяют.docx

• Задание на самоконтроль выберите морфологические проявления гипертрофии.docx

• Методы определения энерготрат человека.docx

• Общие вопросы клинической фармакологии, принципы рациональной фармакотерапии Нежелательные лекарственные реакции. Взаимодействие лекарственных средств Задания для проверки исходного уровня.docx