ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| № | Е1 | Е2 | Е3 | Е4 | Е5 | Е6 | R1 | R2 | R3 | R4 | R5 | R6 | |||||||||||||
| Вар | Сх. | В | Ом | ||||||||||||||||||||||
| 5 | 5 | 15 | 8 | - | 10 | 20 | - | 3 | 2 | 6 | 4 | 8 | 4 | ||||||||||||
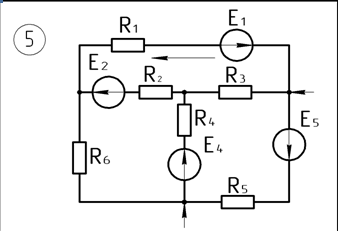
Требуется:
1. Составить уравнения по законам Кирхгофа (не решая их.)
2. Найти токи ветвей методом контурных токов.
3. Найти те же токи методом межузловых напряжений.
4. Составить баланс мощностей для исходной схемы (с источником тока), подставляя в уравнение баланса числовые значения токов ветвей, найденных одним из методов.
5. Результаты расчётов токов ветвей обоими методами свести в таблицу, сравнить между собой и сделать вывод.
6. Найти ток ветви, указанный на схеме стрелкой, пользуясь теоремой об активном двухполюснике (принципом эквивалентного генератора).
7. Построить потенциальную диаграмму для контура, содержащего максимальное число источников ЭДС.
Значение тока источника тока
 =7А.
=7А.Исходная схема:
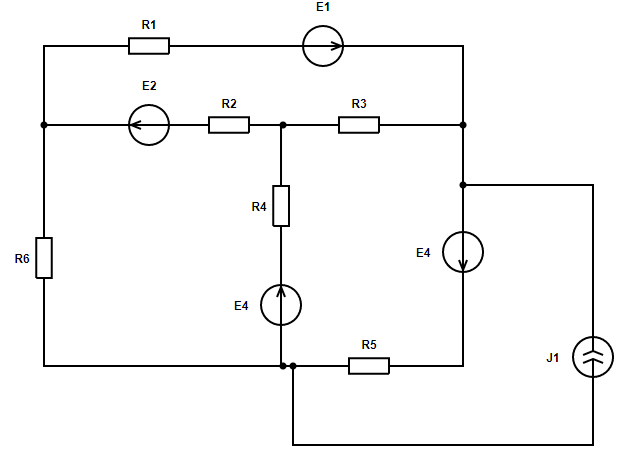
Рассчитаем схему по законам Кирхгофа.
В данной схеме: узлов - 4, ветвей - 7, независимых контуров - 3.
Произвольно зададим направления токов в ветвях и направления обхода контуров.
Принятые направления токов:
Ток I1 направлен от узла '2 у.' к узлу '1 у.' через элементы R1, E1.
Ток I2 направлен от узла '3 у.' к узлу '2 у.' через элементы R2, E2.
Ток I3 направлен от узла '1 у.' к узлу '3 у.' через элементы R3.
Ток I4 направлен от узла '4 у.' к узлу '3 у.' через элементы E4, R4.
Ток I5 направлен от узла '1 у.' к узлу '4 у.' через элементы E4, R5.
Ток I6 направлен от узла '2 у.' к узлу '4 у.' через элементы R6.
Принятые направления обхода контуров:
Контур №1 обходится через элементы R1, E1, R3, R2, E2 в указанном порядке.
Контур №2 обходится через элементы R2, E2, R6, E4, R4 в указанном порядке.
Контур №3 обходится через элементы R3, R4, E4, R5, E4 в указанном порядке.
Составим уравнения по первому закону Кирхгофа. При составлении уравнений "втекающие" в узел токи будем брать со знаком "+", а "вытекающие" - со знаком "-".
Количество уравнений, составляемых по первому закону Кирхгофа, равно Nу−1, где Nу - число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 4 - 1 = 3.
Составим уравнение для узла №1:
I1−I3−I5+J1=0
Составим уравнение для узла №2:
−I1+I2−I6=0
Составим уравнение для узла №3:
−I2+I3+I4=0
Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.
Количество уравнений, составляемых по второму закону Кирхгофа, равно Nв−Nу+1, где Nв - число ветвей без источников тока. Для данной схемы количество уравнений по второму закону Кирхгофа равно 6 - 4 + 1 = 3.
Составим уравнение для контура №1:
R1⋅I1+R3⋅I3+R2⋅I2=E1+E2
Составим уравнение для контура №2:
R2⋅I2+R6⋅I6+R4⋅I4=E2+E4
Составим уравнение для контура №3:
R
3⋅I3−R4⋅I4−R5⋅I5=−E4−E4
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:
I1−I3−I5=−J1
−I1+I2−I6=0
−I2+I3+I4=0
R1⋅I1+R3⋅I3+R2⋅I2=E1+E2
R2⋅I2+R6⋅I6+R4⋅I4=E2+E4
R3⋅I3−R4⋅I4−R5⋅I5=−E4−E4
Рассчитаем схему по методу контурных токов.
В данной схеме: узлов - 4, ветвей без источников тока - 6, независимых контуров - 3.
Количество уравнений, составляемых по методу контурных токов, равно Nв−Nу+1, где Nв - число ветвей без источников тока, Nу - число узлов.
Для данной схемы количество уравнений, составляемых по методу контурных токов, равно 6 - 4 + 1 = 3.
Произвольно зададим направления обхода контуров и соответствующие контурные токи.
Принятые направления обхода контуров:
Контур №1 обходится через элементы R1, E1, R3, R2, E2 в указанном порядке. Через эти элементы протекает контурный ток I11.
Контур №2 обходится через элементы R2, E2, R6, E4, R4 в указанном порядке. Через эти элементы протекает контурный ток I22.
Контур №3 обходится через элементы R3, R4, E4, R5, E4 в указанном порядке. Через эти элементы протекает контурный ток I33.
Дополнительно зададим контурные токи, создаваемые источниками тока.
Контурный ток J11 протекает через элементы J1, E4, R5 в указанном порядке.
Составим уравнения по методу контурных токов.
Составим уравнение для контура №1:
I11⋅(R1+R3+R2)+I33⋅R3+I22⋅R2=E1+E2
Составим уравнение для контура №2:
I22⋅(R2+R6+R4)+I11⋅R2−I33⋅R4=E2+E4
Составим уравнение для контура №3:
I33⋅(R3+R4+R5)+I11⋅R3−I22⋅R4−J11⋅R5=−E4−E4
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми контурными токами. Система уравнений по методу контурных токов для исходной цепи выглядит следующим образом:
I11⋅(R1+R3+R2)+I33⋅R3+I22⋅R2=E1+E2
I22⋅(R2+R6+R4)+I11⋅R2−I33⋅R4=E2+E4
I33⋅(R3+R4+R5)+I11⋅R3−I22⋅R4=−E4−E4+J11⋅R5
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
11⋅I11+2⋅I22+6⋅I33=23
2⋅I11+10⋅I22−4⋅I33=18
6⋅I11−4⋅I22+18⋅I33=26
Решим систему уравнений и получим искомые контурные токи:
Решаем систему в Эксель методом Крамера
| 11 | 2 | 6 | 23 |
| 2 | 10 | -4 | 18 |
| 6 | -4 | 18 | 26 |
| 11 | 2 | 6 |
| 2 | 10 | -4 |
| 6 | -4 | 18 |
Определитель Δ=(11*10*18+2*(-4)*6+2*(-4)*6)-(6*10*6+2*2*18+11*4*4)=1884-608=1276
Далее:
| 23 | 2 | 6 |
| 18 | 10 | -4 |
| 26 | -4 | 18 |
Δ1=(23*10*18+2*(-4)*26+18*4*4)-(26*10*6+18*2*18+23*4*4)=924
| 11 | 23 | 6 |
| 2 | 18 | -4 |
| 6 | 26 | 18 |
Δ2=(11*18*18+2*26*6+23*(-4)*6)-(18*6*6+2*23*18+11*26*(-4))=2992
| 11 | 2 | 23 |
| 2 | 10 | 18 |
| 6 | -4 | 26 |
Δ3=(11*10*26+2*2*26+2*(-4)*23)-(2*2*26+6*10*23+11*(-4)*18)=2200
I11 = Δ1/Δ=924/1276=0.7241 А
I22= Δ2/Δ=2992/1276=2.3448 А
I33= Δ3/Δ=2200/1276=1.7241 А
Произвольно зададим направления токов в ветвях.
Принятые направления токов:
Ток I1 направлен от узла '2 у.' к узлу '1 у.' через элементы R1, E1.
Ток I2 направлен от узла '3 у.' к узлу '2 у.' через элементы R2, E2.
Ток I3 направлен от узла '1 у.' к узлу '3 у.' через элементы R3.
Ток I4 направлен от узла '4 у.' к узлу '3 у.' через элементы E4, R4.
Ток I5 направлен от узла '1 у.' к узлу '4 у.' через элементы E4, R5.
Ток I6 направлен от узла '2 у.' к узлу '4 у.' через элементы R6.
Рассчитаем токи в ветвях исходя из полученных контурных токов.
I1=I11=0.7241
I2=I11+I22=0.7241+2.3448=3.0690
I3=I11+I33=0.7241+1.7241=2.4483
I4=I22−I33=2.3448−1.7241=0.6207
I5=−I33+J1=−1.7241+7=5.2759
I6=I22=2.3448
Рассчитаем схему по методу узловых потенциалов.
В данной схеме: узлов - 4, ветвей - 7, из них особых ветвей - 0. Под особыми ветвями понимаются ветви, в которых имеется только источники ЭДС.
Количество уравнений, составляемых по методу узловых потенциалов, равно Nу−1−Ne, где Nу - число узлов, Ne - число особых ветвей. Для данной схемы количество уравнений, составляемых по методу узловых потенциалов, равно 4 - 1 - 0 = 3.
В исходной схеме нет особых ветвей. Примем потенциал узла №1 равным нулю, т.е. φ1=0 В
Составим уравнения для определения потенциалов остальных узлов.
Уравнение для узла №2:
φ2⋅(1/R1+1/R2+1/R6)−φ1⋅1/R1−φ3⋅1/R2−φ4⋅1/R6=−E1⋅1/R1+E2⋅1/R2
Уравнение для узла №3:
φ3⋅(1/R2+1/R3+1/R4)−φ2⋅1/R2−φ1⋅1/R3−φ4⋅1/R4=−E2⋅1/R2+E4⋅1/R4
Уравнение для узла №4:
φ4⋅(1/R4+1/R5+1/R6)−φ3⋅1/R4−φ1⋅1/R5−φ2⋅1/R6=−E4⋅1/R4+E4⋅1/R5−J1
Перенесём все известные слагаемые в правую часть и объединим полученные уравнения в систему. Получим: