ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
φ2⋅(1/R1+1/R2+1/R6)−φ3⋅1/R2−φ4⋅1/R6=φ1⋅1/R1−E1⋅1/R1+E2⋅1/R2
φ3⋅(1/R2+1/R3+1/R4)−φ2⋅1/R2−φ4⋅1/R4=φ1⋅1/R3−E2⋅1/R2+E4⋅1/R4
φ4⋅(1/R4+1/R5+1/R6)−φ3⋅1/R4−φ2⋅1/R6=φ1⋅1/R5−E4⋅1/R4+E4⋅1/R5−J1
Подставим в полученную систему уравнений численные значения и получим:
1.0833⋅φ2−0.5000⋅φ3−0.2500⋅φ4=−1
−0.5000⋅φ2+0.9167⋅φ3−0.2500⋅φ4=−1.5000
−0.2500⋅φ2−0.2500⋅φ3+0.6250⋅φ4=−7
Решим систему уравнений и получим искомые потенциалы узлов:
Находим определители
| 1,0833 | -0,5 | -0,25 |
| -0,5 | 0,9167 | -0,25 |
| -0,25 | -0,25 | 0,625 |
Δ=0,2769
| -1 | -0,5 | -0,25 |
| -1,5 | 0,9167 | -0,25 |
| -7 | -0,25 | 0,625 |
Δ2= -3,552
| 1,0833 | -1 | -0,25 |
| -0,5 | -1,5 | -0,25 |
| -0,25 | -7 | 0,625 |
Δ3 =-4,0676
| 1,0833 | -0,5 | -1 |
| -0,5 | 0,9167 | -1,5 |
| -0,25 | -0,25 | -7 |
Δ4=-6,149
φ2=-3,552/0,2679=−12.8276 В
φ3=-4,0676/0,279=−14.6897 В
φ4=-6,149/0,2679=−22.2069 В
Произвольно зададим направления токов в ветвях.
Принятые направления токов:
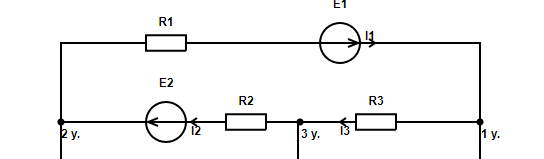
Ток I1 направлен от узла '2 у.' к узлу '1 у.' через элементы
R1, E1.
Ток I2 направлен от узла '3 у.' к узлу '2 у.' через элементы R2, E2.
Ток I3 направлен от узла '1 у.' к узлу '3 у.' через элементы R3.
Ток I4 направлен от узла '4 у.' к узлу '3 у.' через элементы E4, R4.
Ток I5 направлен от узла '1 у.' к узлу '4 у.' через элементы E4, R5.
Ток I6 направлен от узла '2 у.' к узлу '4 у.' через элементы R6.
Определим токи во всех ветвях, кроме особых, по закону Ома для участка цепи:
I1= (φ2−φ1+E1)/ R1=(−12.8276−0+15)/3=0.7241 А
I2= (φ3−φ2+E2)=((−14.6897)−(−12.8276)+8)/2=3.0690 А
I3=( φ1−φ3)/ R3=(0−(−14.6897))/6=2.4483 А
I4=( φ4−φ3+E4)/ R4=((−22.2069)−(−14.6897)+10)/4=0.6207 А
I5=( φ1−φ4+E4)/ R5=(0−(−22.2069)+20)/8=5.2759 А
I6=( φ2−φ4)/ R6=((−12.8276)−(−22.2069))/4=2.3448 А
Результаты из полученных контурных токов.
I1=I11=0.7241
I2=I11+I22=0.7241+2.3448=3.0690
I3=I11+I33=0.7241+1.7241=2.4483
I4=I22−I33=2.3448−1.7241=0.6207
I5=−I33+J1=−1.7241+7=5.2759
I6=I22=2.3448
Видим, что результаты аналогичны.
Проверим баланс мощностей.
Определим мощность, потребляемую приёмниками:
Рпр=R1⋅∣I1∣2+R2⋅∣I2∣2+R3⋅∣I3∣2+R4⋅∣I4∣2+R5⋅∣I5∣2+R6⋅∣I6∣2.
Подставим числовые значения и получим:
Рпр=3⋅0.72412+2⋅3.06902+6⋅2.44832+4⋅0.62072+8⋅5.27592+4⋅2.34482=302.5862.
Определим мощность, отдаваемую источниками:
Рист=РE+РJ,
где РE - мощность, отдаваемая источниками ЭДС, РJ - мощность, отдаваемая источниками тока.
Определим мощность РE, отдаваемую источниками ЭДС:
РE=E1⋅I1+E2⋅I2+E4⋅I4+E4⋅I5.
Подставим числовые значения и получим:
РE=15⋅0.7241+8⋅3.0690+10⋅0.6207+20⋅5.2759=147.1379.
Определим мощность РJ, отдаваемую источниками тока.
Определим мощность РJ1, отдаваемую источником тока J1:
РJ1=UJ1⋅J1.
Определим напряжение на источнике тока J1, обозначенное как UJ1. Для этого рассмотрим контур, проходящий через элементы J1, E4, R5 в указанном порядке, и составим для этого контура уравнение по второму закону Кирхгофа. Получим:
−UJ1+R5⋅I5=E4.
Выразим из полученного уравнения напряжение UJ1 и подставим числовые значения. Получим:
UJ1=R5⋅I5−E4=22.2069
Мощность, отдаваемая источником тока J1, равна:
РJ1=UJ1⋅J1=22.2069⋅7=155.4483.
Суммарная мощность, отдаваемая источниками тока, равна:
SJ=SJ1=155.4483
Мощность, отдаваемая источниками, равна:
Рист=РE+РJ=147.1379+155.4483=302.5862.
Итак, Рпр=302.5862, Рист=302.5862. Баланс мощностей сходится.
Рассчитаем ток I в ветви с элементами R1, E1 по методу эквивалентного генератора. Для этого рассчитаем напряжение холостого хода на выводах разомкнутой ветви с искомым током и эквивалентное сопротивление пассивной цепи относительно ветви с искомым током.
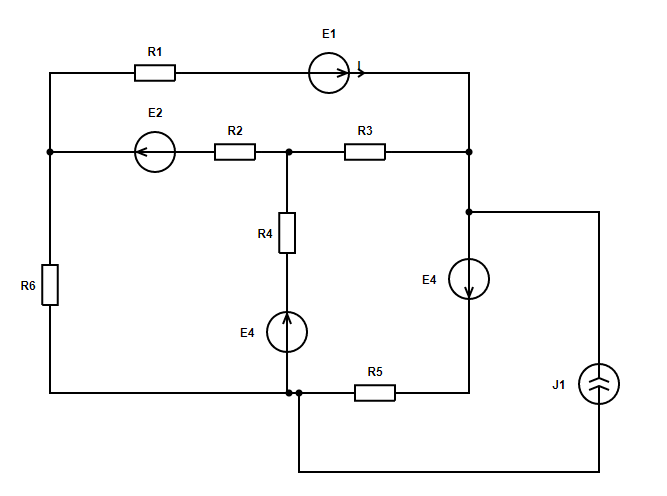
Рассчитаем напряжение холостого хода. На рисунке ниже приведена рассчитываемая схема. Напряжение холостого хода Uхх сонаправлено с искомым током. Принятое направление искомого тока приведено на схеме выше.
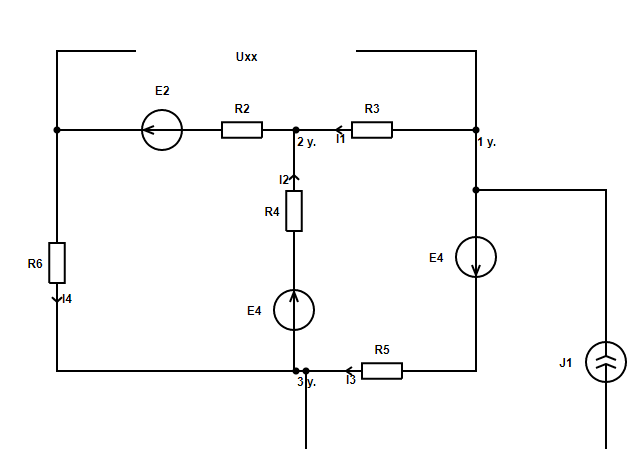
Рассчитаем схему по законам Кирхгофа.
В данной схеме: узлов - 3, ветвей - 5, независимых контуров - 2.
Произвольно зададим направления токов в ветвях и направления обхода контуров.
Принятые направления токов:
Ток I1 направлен от узла '1 у.' к узлу '2 у.' через элементы R3.
Ток I2 направлен от узла '3 у.' к узлу '2 у.' через элементы E4, R4.
Ток I3 направлен от узла '1 у.' к узлу '3 у.' через элементы E4, R5.
Ток I4 направлен от узла '2 у.' к узлу '3 у.' через элементы R2, E2, R6.
Принятые направления обхода контуров:
Контур №1 обходится через элементы R3, R4, E4, R5, E4 в указанном порядке.
Контур №2 обходится через элементы E4, R4, R2, E2, R6 в указанном порядке.
Составим уравнения по первому закону Кирхгофа. При составлении уравнений "втекающие" в узел токи будем брать со знаком "+", а "вытекающие" - со знаком "-".
Количество уравнений, составляемых по первому закону Кирхгофа, равно Nу−1, где Nу - число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 3 - 1 = 2.
Составим уравнение для узла №1:
−I1−I3+J1=0
Составим уравнение для узла №2:
I1+I2−I4=0
Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.
Количество уравнений, составляемых по второму закону Кирхгофа, равно Nв−Nу+1, где Nв - число ветвей без источников тока. Для данной схемы количество уравнений по второму закону Кирхгофа равно 4 - 3 + 1 = 2.
Составим уравнение для контура №1:
R3⋅I1−R4⋅I2−R5⋅I3=−E4−E4
Составим уравнение для контура №2:
R4⋅I2+(R2+R6)⋅I4=E4+E2
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:
−I1−I3=−J1
I1+I2−I4=0R3⋅I1−R4⋅I2−R5⋅I3=−E4−E4
R4⋅I2+(R2+R6)⋅I4=E4+E2
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
−I1−I3=−7
I1+I2−I4=0
6⋅I1−4⋅I2−8⋅I3=−30
4⋅I2+6⋅I4=18
Решим систему уравнений и получим искомые токи:
I1=2.0244 А
I2=0.5854 А
I3=4.9756 А
I4=2.6098 А
Определим искомое напряжение холостого хода. Рассмотрим контур, проходящий в указанном порядке через элементы Uхх, R3, R2, E2, и составим для него уравнение по второму закону Кирхгофа. Получим:
Uхх+I1⋅R3+I4⋅R2=E2
Определим напряжение холостого хода. Получим:
Uхх=−I1⋅R3−I4⋅R2+E2=−2.0244⋅6−2.6098⋅2+8=−9.3659 В
Рассчитаем внутреннее сопротивление цепи Zвн относительно ветви с искомым током. Для этого из исходной схемы уберём ветвь с искомым током, при этом оставим концы этой ветви. Все источники ЭДС закоротим, а источники тока разомкнем.
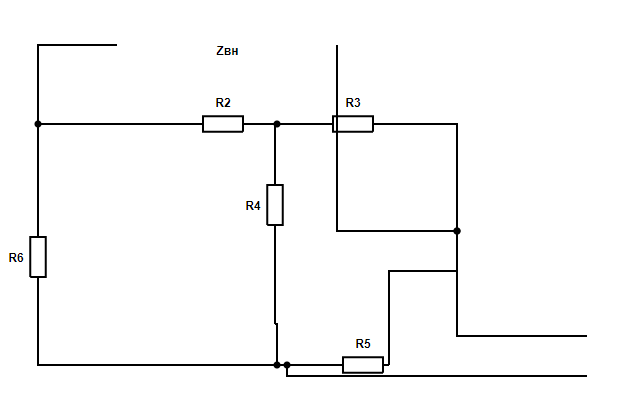
Рассчитаем эквивалентное сопротивление цепи относительно ветви с искомым током.
Ветвь с элементами R2; ветвь с элементами R3; ветвь с элементами R4 соединены в звезду. Преобразуем её в треугольник. Получим сопротивления треугольника:
Z21=R2+R3+ R2⋅R3/ R4=2+6+2⋅6/4=11
Z14=R3+R4+ R3⋅R4/ R2=6+4+6⋅4/2=22
Z42=R4+R2+ R4⋅R2/ R3=4+2+4⋅2/6=7.3333
Ветвь с элементами R5 параллельна ветви с элементами Z14. Эквивалентное сопротивление этих ветвей равно:
Z1= R5⋅Z14/( R5+Z14 )= 8⋅22/(8+22 )=5.8667
Ветвь с элементами R6 параллельна ветви с элементами Z42. Эквивалентное сопротивление этих ветвей равно:
Z2= R6⋅Z42/( R6+Z42 )= 4⋅7.3333/(4+7.3333 )=2.5882
Ветвь с элементами Z1 последовательна ветви с элементами Z2. Эквивалентное сопротивление этих ветвей равно:
Z3=Z1+Z2=5.8667+2.5882=8.4549
Ветвь с элементами Z21 параллельна ветви с элементами Z3. Эквивалентное сопротивление этих ветвей равно:
Z4= Z21⋅Z3/( Z21+Z3 )=11⋅8.4549/(11+8.4549)=4.7805
Внутреннее сопротивление цепи равно:
Zвн=Z4+0=4.7805+0=4.7805 Ом
Определим искомый ток:
I= (Uхх+E1)/ (Zвн+R1) =(−9.3659+15)/( 4.7805+3)=0.7241 А
В данной схеме три контура, содержащих по две ЭДС. Выберем контур
R1,E1,R3,R2,E2
Строим потенциальную диаграмму.
| φ1 | 0 |
| φ1+I3*R3 | -14,687 |
| φ3-I2*R2 | -20,828 |
| φ3-I2*R2+φ2 | -12,828 |
| φ2-I1*R1 | -15 |
| φ2-I1*R2+E1 | 0 |