Файл: 2 Размещения с повторениями и без повторений Определение.doc
Добавлен: 03.12.2023
Просмотров: 1829
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.2. Размещения с повторениями и без повторений
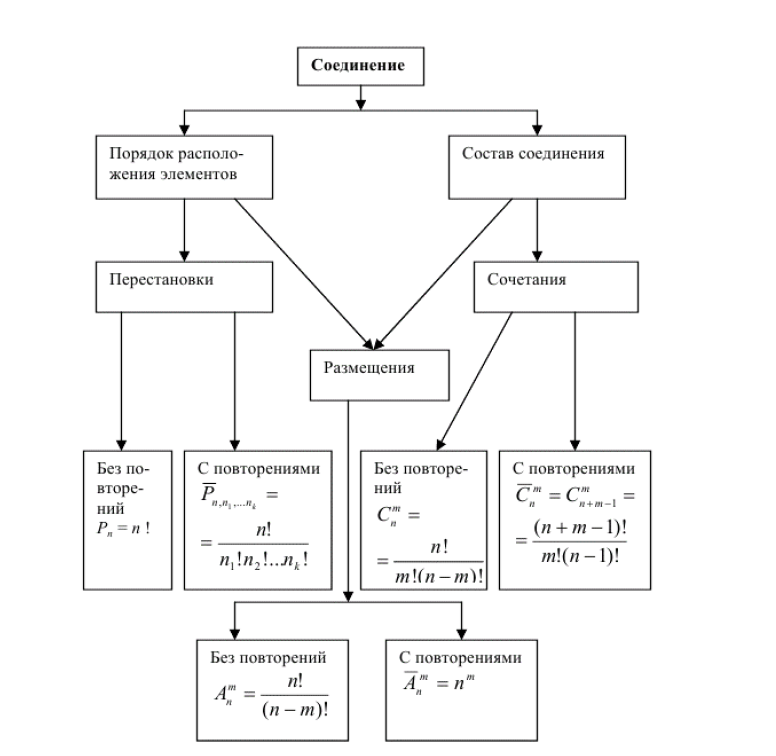
Определение. Размещениями из n элементов по m называются соединения из n элементов по m, которые отличаются друг от друга либо своими элементами (составом), либо порядком их расположения.
Термин «упорядоченная» означает, что порядок следования элементов в выборке существенен: выборки с одними и теми же элементами, но с разным порядком их следования различны.

Задача. Пусть имеется множество, содержащее 4 буквы: {А, В, С, D}. Записать все возможные размещения из 4 указанных букв по две: а) без повторений; б) с повторениями.
Задача. Пусть имеется множество, содержащее 2 буквы {А, B}. Записать все возможные размещения с повторениями из 4-х букв.
Задача. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Задача. У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера – составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Задача. Телефонная книга раскрывается наудачу и выбирается случайный номер телефона, который состоит из 7 цифр. Сколько существует вариантов выбора при условии: а) все цифры номера различны; б) все цифры номера могут быть любыми из имеющихся десяти; в) четыре последние цифры телефонного номера одинаковы.
2.3. Перестановки без повторений
Определение. Размещения, в которых участвуют все n элементов генеральной совокупности, называются перестановками без повторений из n элементов. Перестановки состоят из одних и тех же элементов, но отличаются между собой порядком.

2.4. Перестановки с повторениями
Определение. Перестановками с повторениями называются
соединения из генеральной совокупности, каждое из которых содержит
n элементов, среди которых элемент
1 a повторяется 1 n раз,
2 a повторяется 2 n раз,
. . . . . . . . . . . . . . . . . . .
n a повторяется k n раз
1 n + 2 n + ... + k n = n
и которые отличаются друг от друга только порядком расположения
различных элементов.

Задача. Пусть имеется множество букв {А, В, С}. Записать все возможные перестановки.
Задача. Сколько можно составить четырехбуквенных «слов» из букв слова «брак»?
Задача. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?
Задача. Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
2.5. Сочетания без повторений
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов?
Определение. Сочетаниями из n различных элементов по m называются соединения из n элементов по m (m n), которые отличаются друг от друга только составом элементов.


2.6. Сочетания с повторениями
Определение. Сочетаниями с повторениями называются соединения из n элементов по m (выбор с возвращением m элементов), которые отличаются только составом и при этом отдельные соединения могут содержать повторяющиеся элементы.
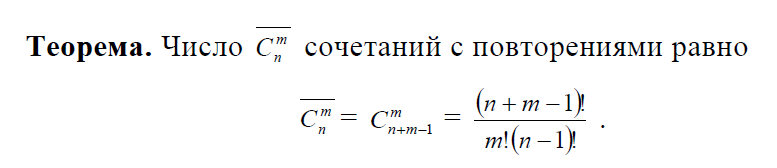
Задача. Пусть имеется множество, содержащее 4 буквы {А, B, С, D}. Запишем все возможные сочетания из указанных букв по 3.
Задача. Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Задача. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?
Задача. Сколько существует вариантов опроса 11 учащихся на одном занятии, если ни одни из них не будет подвергнут опросу дважды и на занятии может быть опрошено любое количество учащихся, причем порядок, в котором опрашиваются учащиеся, безразличен?
Задача. Имеются 2 буквы A, 2 буквы B, 2 буквы C. Сколькими способами можно выбрать две из этих шести букв?
Задача. В технической библиотеке имеются книги по математике, физике, химии и т. д., всего по 16 разделам науки. Поступили очередные 4 заказа на литературу. Сколько существует вариантов такого заказа?
Задача. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
2.8. Рекомендации по решению задач
Решение комбинаторных задач представляет известную трудность для начинающих. Причин много, но одна из них очевидна - при изложении комбинаторики используется своя специфическая терминология (генеральная совокупность, выборка, правила выбора). В задаче же этих терминов, как правило, нет – сформулирована она на обычном литературном языке и комбинаторные понятия присутствуют в ней в неявной форме. Поэтому после усвоения содержания задачи нужно ее «перевести» на математический язык.
Для этого необходимо выяснить,
1) что является генеральной совокупностью - она всегда будет присутствовать в задаче, т. е. комбинаторные задачи связаны с выбором объектов, а этот выбор из чего-то (генеральной совокупности) производится; каков объем генеральной совокупности;
2) одна или несколько генеральных совокупностей;
3) что является выборкой и каков объем выборки;
4) правила выбора: допустимы или нет повторы, важен ли порядок выбираемых элементов, возможно ли изменение состава.
После этого полезно для себя переформулировать задачу на языке генеральных совокупностей и выборок. В зависимости от ситуации выбрать нужную формулу (см. таблицу). Иногда в более сложных задачах приходится использовать совместно несколько формул.
БАНК ЗАДАЧ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Имеется множество чисел {1, 2, 3, 4}. Составить следующие виды соединений по 2 элемента из четырех: а) размещения без повторений; б) размещения с повторениями; в) сочетания без повторений; г) сочетания с повторениями.
2. Из Москвы до Новосибирска можно добраться поездом и самолетом; из Новосибирска в Томск - поездом, самолетом, автобусом, пароходом. Сколькими способами можно осуществить путешествие по маршруту Москва - Новосибирск-Томск?
Ответ: 8.
3. На вершину горы ведет 7 дорог. Сколькими способами турист может подняться на гору и спуститься с нее? Дайте ответ на этот же вопрос, если подъем и спуск осуществляются различными путями.
Ответ: 49
4. Стадион имеет 4 входа. Сколькими способами болельщик может войти на стадион в один вход, а выйти через другой?
Ответ: 12.
5. В корзине лежат 12 яблок и 10 апельсинов. Ваня выбирает из нее яблоко или апельсин, после чего Надя берет и яблоко и апельсин. В каком случае Надя имеет большую свободу выбора: если Ваня взял яблоко или если он взял апельсин?
Ответ. Если взято яблоко.
6. Сколько четырехзначных чисел можно составить из цифр 0, 1,2, 3, 4, 5, если:
а) ни одна из цифр не повторяется более одного раза;
б) цифры могут повторяться;
в) числа должны быть нечетными (цифры могут повторяться)?
Ответ: а) 300; б) 1080; в) 540.
7. Сколькими способами можно разместить 4 книги на полке?
Ответ: 24.
8. Сколькими способами можно поставить в ряд 6 человек для выполнения их группового портрета? Сколькими способами можно это сделать, если поставить трех человек в переднем ряду и трех во втором?
Ответ: 720.
9. Сколько различных «слов» можно составить, переставляя буквы слова «лодка»?
Ответ: 120.
10. Сколько различных «слов» можно составить, переставляя буквы слова «математика»?
Ответ: 151200.
11. Сколько различных слов можно составить, переставляя буквы слова «комбинаторика»?
Ответ: 389188800.
12. В классе изучают 10 предметов. В понедельник 6 уроков, причем все уроки разные. Сколькими способами можно составить расписание на понедельник?
Ответ: = 151200. 6 10 A
13. Сколькими способами можно выбрать трех делегатов на студенческую конференцию из группы в 20 человек?
Ответ: 1140.
14. Пассажир оставил вещи в автоматической камере хранения, а когда пришел получить вещи, выяснилось, что он забыл номер. Он только помнит, что в номере были числа 23 и 37. Чтобы открыть камеру, нужно правильно набрать пятизначный номер. Какое наибольшее количество номеров нужно перебрать, чтобы открыть камеру?
Ответ: 60.
15. Сколькими способами можно выбрать три различные краски из имеющихся пяти?
Ответ: 10.
16. Сколькими способами можно составить трехцветный флаг, если материал пяти различных цветов?
Ответ
: 60.
17. В театре 10 актеров и 8 актрис. Сколькими способами можно распределить между ними роли в пьесе, в которой 5 мужских и 3 женские роли?
Ответ: · = 10160640. 5 10 A 3 8 A
18. Из колоды в 52 карты выбирают 3. Сколькими способами может быть сделан выбор «тройка, семерка, туз»?
Ответ: 64.
19. На олимпиаду пришло 8 студентов. Сколькими способами их можно распределить в 3 аудитории?
Ответ: 6501 = 3 . 8
20. Сколькими способами можно распределить 10 специалистов по четырем цехам, чтобы в них попало соответственно 1, 2, 3, 4 специалиста?
Ответ: 12600.
21. Сколькими способами можно расселить 8 студентов по трем комнатам: одноместной, трехместной и четырехместной?
Ответ: 280.
22. Учителю для урока труда нужно принести 28 листов цветной бумаги. В учительской имеется белая, синяя, красная, зеленая и желтая бумага. Сколькими способами учитель может выбрать нужные ему 28 листов?
Ответ: 35960.
23. Сколькими способами можно выбрать 6 одинаковых или разных пирожных в кондитерской, где есть 11 разных сортов пирожных?
Ответ: 8008.
24. Сколько существует шестизначных чисел, все цифры которых нечетны (1,3, 5, 7, 9)?
Ответ: 15625.
25. Сколькими способами можно рассадить 7 человек за круглым столом?
Ответ: 5040.
26. Семь девушек водят хоровод. Сколькими различными способами они могут встать в круг?
Ответ: 720.
27. Восемь девушек отправились в путешествие на двух лодках, в меньшей из которых могли поместиться не более четырех, а в большей - не более шестерых. Сколькими различными способами они могут распределиться в разные лодки? (Распределения считаются различными, если хотя бы одна из девушек окажется в другой лодке.)
Ответ: + + = 154. 2 8 C 3 8 C 4 8 C
28. В классе 29 учеников. Сколько существует различных вариантов присутствия (отсутствия) этих учеников в классе?
Ответ: 229.
29. Числа 1, 2,..., 9 записываются в случайном порядке. Сколько существует вариантов такой записи, если: а) числа будут записаны в порядке возрастания: б) числа 1 и 2 будут стоять рядом и в порядке возрастания; в) на четных местах будут стоять четные числа; г) сумма каждых двух чисел, стоящих на одинаковом расстоянии от концов, равна 10?
Ответ: а) 1; 2) 8! = 40320; в) 5! 4! = 2880; г) 8 · 6 · 4 · 2 = 384.
30. Сколько четных пятизначных чисел можно составить из цифр 1, 2? Ответ: 16.
ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ
Вариант 1