Файл: Для каждого из районов (в каждой задаче) требуется.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.12.2023

Просмотров: 51

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Вариант 16

Экономист, изучая зависимость выработки Y (тыс. руб.) от объема X (тыс. руб.) товарооборота, обследовал по 10 магазинов, торгующих одинаковым ассортиментом товаров в 5 районах. Полученные данные отражены в таблице 1.

Для каждого из районов (в каждой задаче) требуется:

• найти коэффициенты корреляции между X и Y .

• построить регрессионные функции линейной зависимости Y = a + b * X фактора Y от фактора X и исследовать их на надежность по критерию Фишера при уровне значимости 0,05;

• найти коэффициент эластичности Y по X при среднем значении X ;

• определить надежность коэффициентов регрессии по критерию Стьюдента:

• найти доверительные интервалы для коэффициентов регрессии;

• построить график регрессионной функции и диаграмму рассеяния;

• используя полученное уравнение линейной регрессии, оценить ожидаемое среднее значение признака Y при X = 100 тыс. руб.

Таблица 1

Исходные данные. Вариант 16

X

тыс. руб.

Y

тыс. руб.

70

2,8

110

3,5

85

2,4

65

2,1

100

3,4

90

3,2

I20

3,6

80

2,5

130

4,1

110

3,3


Решение

1) Вычислим коэффициент корреляции между X и Y по формуле:



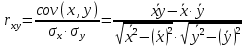
Произведем необходимые расчеты в таблице:

Таблица 2
x
y
x*y
x²
у²
yx
y-yx
(y-yx)2
Ai, %

1
2
3
6
4
5
7
8
9
10

1
70
2,8
196
4900
7,84
2,401
0,399
0,160
14,26

2
110
3,5
385
12100
12,25
3,461
0,039
0,002
1,11

3
85
2,4
204
7225
5,76
2,798
-0,398
0,159
16,60

4
65
2,1
136,5
4225
4,41
2,268
-0,168
0,028
8,00

5
100
3,4
340
10000
11,56
3,196
0,204
0,042
6,00

6
90
3,2
288
8100
10,24
2,931
0,269
0,072
8,41

7
120
3,6
432
14400
12,96
3,726
-0,126
0,016
3,51

8
80
2,5
200
6400
6,25
2,666
-0,166
0,027
6,63

9
130
4,1
533
16900
16,81
3,992
0,108
0,012
2,65

10
110
3,3
363
12100
10,89
3,461
-0,161
0,026
4,89

Сумма
960
30,9
3077,5
96350
98,97
30,900
0,000
0,543
72,05

Ср.знач.
96
3,09
307,75
9635
9,897
3,09
-
0,05
7,20

Используя средние значения, вычисленные в таблице 2, найдем коэффициент корреляции между X и Y:



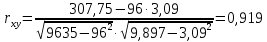
Близость коэффициента корреляции к 1 указывает на тесную линейную связь между признаками.
2) Построим регрессионные функции линейной зависимости 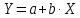фактора Y от фактора X. Используя данные таблицы 2, вычислим неизвестные коэффициенты находим по формулам (по методу наименьших квадратов):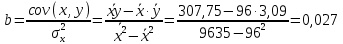





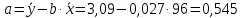
Построенное уравнение регрессииY (издержки обращения) на X (объем товарооборота):



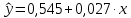
- если объем товарооборота увеличится на 1000 р., то выработка возрастет на 0,027 тыс. руб. (то есть на 27 руб.).

Коэффициент детерминации 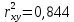показывает, что уравнением регрессии объясняется 84,4% дисперсии результативного признака, а на долю прочих факторов приходится 15,6%.

Оценим качество уравнения регрессии в целом с помощью F –критерия Фишера. Сосчитаем фактическое значение F -критерия:



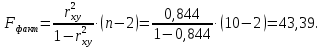
Табличное значение: 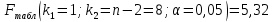. Так как 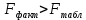, то признается статистическая значимость уравнения в целом.
3) Вычислим коэффициент эластичности Y по X при среднем значении X:



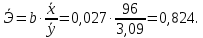
Вывод: если объем товарооборота увеличится на 1%, то выработка возрастет на 0,824%.
4) Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитаем t -критерий Стьюдента. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции.











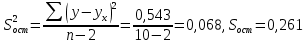
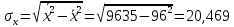
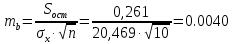
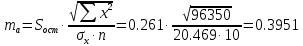
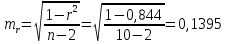
Фактические значения t -статистик:



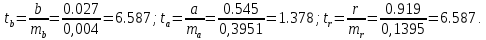
Табличное значение t -критерия Стьюдента при α=0,05 и числе степеней свободы 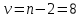есть .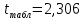

Так как 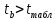и 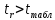, то признаем статистическую значимость параметра регрессии b и показателя тесноты связи.

Так как 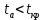, то параметр 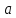статистически не значим.
5) Рассчитаем доверительные интервалы для параметров регрессии a и b:

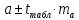и .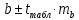

Получим, что 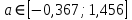и .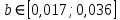

Так как в границы доверительного интервала параметра a попадает ноль, то подтверждается его незначимость.

В границы доверительного интервала параметра b ноль не попадает, подтверждается его значимость.

Средняя ошибка аппроксимации (по последнему столбцу расчетной таблицы 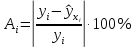) 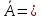7,21% говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.
6) Построим график регрессионной функции и диаграмму рассеяния.



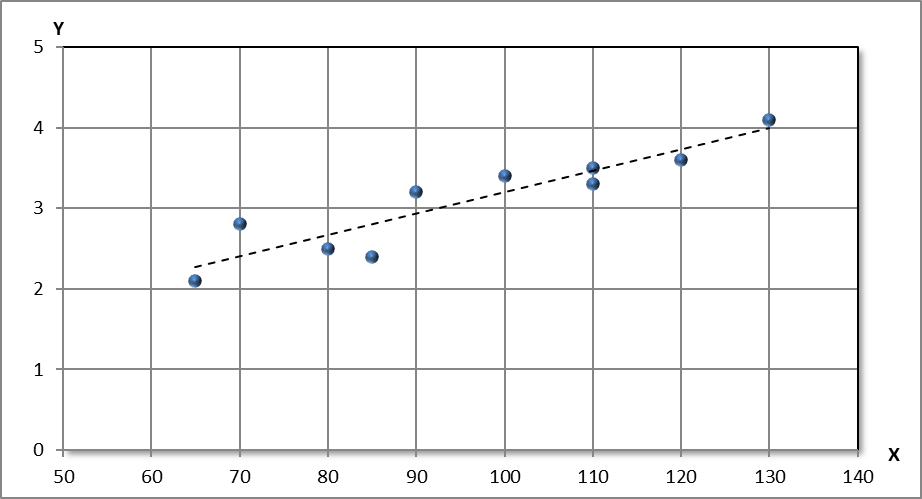
Рис.1. Линейная модель

7) Используя полученное уравнение линейной регрессии, оценим ожидаемое среднее значение признака Y при X = 100 тыс. руб.





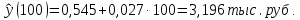
Вывод: построенная линейная модель, позволяет предположить, что при объеме товарооборота 100 тыс. руб. выработка будет составлять 3,196 тыс.руб.


Найдем доверительный интервал прогноза. Ошибка прогноза



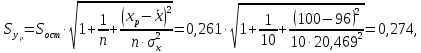
а доверительный интервал ( ):



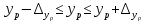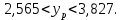
Т.е. прогноз является статистически надежным.

Вывод: с вероятностью 95% можно утверждать, что при товарообороте в объеме 100 тыс. руб. выработка будет находится в границах от 2,565 до 3,827 тыс. руб.

Смотрите также файлы