Файл: 8 Радиопередатчики с угловой модуляцией 1 Общие сведения об угловой модуляции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 57
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
8 Радиопередатчики с угловой модуляцией
8.1 Общие сведения об угловой модуляции
При изучении амплитудной модуляции в разделе 6, передача информации осуществлялась путём изменения амплитуды несущего колебания в соответствии с передаваемым сигналом. Представим теперь несущее колебание в следующем виде
u(t)=Ucos(ωt+φ)= UcosФ(t) (8.1)
Очевидно, что в соответствии с передаваемой информацией, помимо амплитуды, можно менять частоту ω или фазу φ, осуществляя, таким образом, частотную или фазовую модуляцию (ЧМ, ФМ). Согласно (8.1) в обоих случаях будет меняться угловой аргумент косинуса Ф(t), поэтому частотную и фазовую модуляцию объединяют общим термином «угловая модуляция». Тем не менее, как будет показано ниже, между ЧМ и ФМ есть и существенные различия.
Воспользуемся простейшей моделью информационного сигнала в форме (6.1). Тогда колебание с частотной модуляцией можно представить в следующем виде
u(t)=Ucos[(ω+ΔωcosΩt)t+φо] (8.2)
В этом выражении Δω – амплитуда отклонения частоты при ЧМ, получившая название – девиация частоты; φо – произвольная постоянная, соответствующая фазовому сдвигу при t = 0. Согласно (6.1) и (8.1)
Δω=Кчм·UΩ(8.3)
Здесь Кчм - крутизна характеристики частотного модулятора.
Аналогично для фазовой модуляции получим
u(t)=Ucos(ωt+ΨcosΩt+φο) (8.4)
В этом выражении Ψ – амплитуда отклонения фазы, названная индексом модуляции. По аналогии с (8.3)
Ψ=Кфм·UΩ(8.5)
Где Кфм - крутизна характеристики фазового модулятора.
Частота и фаза гармонического колебания связаны следующими соотношениями
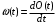 (8.6)
(8.6)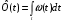 (8.7)
(8.7)Используя эти зависимости можно определить связь между ЧМ и ФМ.
Подставив значение Ф(t) из (8.4) в (8.6), определим как изменяется частота при ФМ
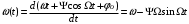 (8.8)
(8.8)Сравнивая частоту в выражениях (8.2) и (8.8), с учётом (8.5), получим
Δω(ФМ) = ΨΩ = Ω·Кфм·UΩ(8.9)
Таким образом, девиация частоты при ФМ
пропорциональна амплитуде информационного сигнала и его частоте, в отличие от (8.3). Поэтому, в информационном сигнале, переданном фазовой модуляцией и принятым частотным детектором, произойдёт подъём верхних частот (исказится амплитудно-частотная характеристика).
Подставим теперь частоту из (8.2) в (8.7) и определим как меняется фаза при ЧМ .
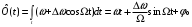 (8.10)
(8.10)Сравнивая фазу в (8.4) с (8.10), с учётом (8.3), получим

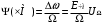 (8.11)
(8.11)В этом случае, индекс модуляции при ЧМ пропорционален амплитуде информационного сигнала и обратно пропорционален его частоте, в отличие от (8.5). Поэтому, в информационном сигнале, переданном частотной модуляцией и принятом фазовым детектором, произойдёт завал верхних частот.
Рассмотренные отличия проявляются только в случае реальных информационных сигналов с меняющейся частотой Ω. Для его модели (6.1) с постоянной частотой, различие между ЧМ и ФМ полностью отсутствует.
На основании (8.9) и (8.11) возможно взаимное преобразование ЧМ в ФМ и наоборот, обеспечив необходимую зависимость (или независимость) индекса модуляции от частоты модулирующего сигнала.
В частности, для преобразования ФМ в ЧМ, необходимо амплитуду модулирующего сигнала изменять обратно пропорционально его частоте. Это может быть выполнено с помощью интегрирующей RC цепи, через которую перед модуляцией должен быть пропущен модулирующий сигнал (см. рисунок 8.1а).
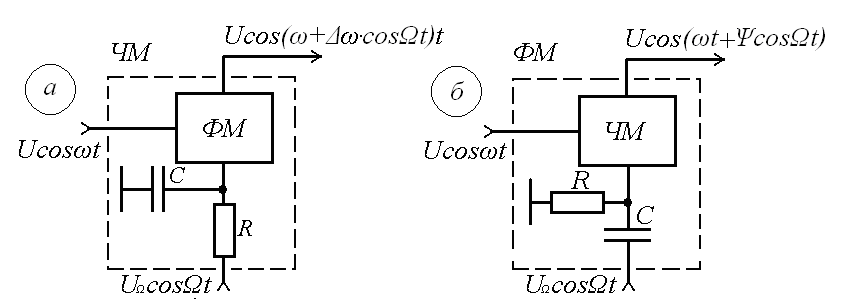
Рисунок 8.1 – Преобразование видов угловой модуляции
Действительно, коэффициент передачи такой цепи
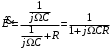 . При условии R>>ΩмаксС
. При условии R>>ΩмаксС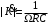 (8.12)
(8.12)Аналогично при использовании дифференцирующей цепи на входе частотного модулятора можно получить фазовую модуляцию (см. рис. 9.1б).
8.2 Спектр сигнала с угловой модуляцией
Для анализа спектра сигнала с угловой модуляцией, воспользуемся выражением (9.4), положив φο=0. Сигнал такого вида раскладывается в ряд Фурье по функциям Бесселя следующим образом
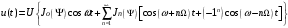 (8.13)
(8.13)Здесь Jn(Ψ) – функция Бесселя первого рода n – го порядка, аргументом которой является индекс модуляции Ψ.
Согласно (8.13), спектр сигнала с угловой модуляцией теоретически бесконечен . Форма огибающей спектра определяется зависимостью функций Бесселя от индекса модуляции. Графики первых четырёх функций Бесселя представлены на рисунке 8.2. Особенностью этих функций является затухающий колебательный характер, поэтому при некоторых значениях Ψ, указанных на рисунке 8.2, несущая частота (Jo) исчезает. В связи с этим, термин «несущая», при рассмотрении угловой модуляции, заменяют термином «средняя частота». Первый максимум функций Бесселя, начиная с n=1 , соответствует Ψ=n+1.
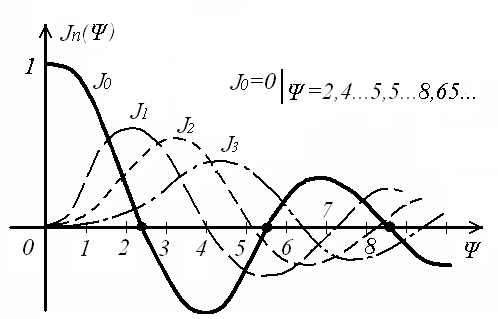
Рисунок 8.1 – Функции Бесселя
Затухающий характер функций Бесселя позволяет на практике без последствий ограничивать полосу занимаемых частот на уровне составляющих, амплитуда которых не превышает 1% от немодулированной несущей.
Эффективную полосу сигнала с угловой модуляцией в этом случае определяют эмпирической формулой
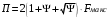 (8.14)
(8.14)В последнем выражении Fмакс – максимальная частота модулирующего сигнала.
На рисунке 8.3 в качестве примера представлены спектры для некоторых значений Ψ[9].
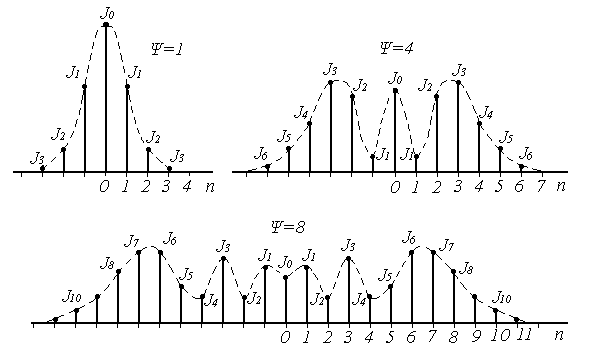
Рисунок 8.3 – Спектры сигналов с угловой модуляцией.
Как уже отмечалось выше, при угловой модуляции одним гармоническим тоном, различия между ФМ и ЧМ нет, т.к индекс модуляции в этом случае величина постоянная. Иначе обстоит дело при модуляции сложным многочастотным сигналом. Поясним это на следующем примере. Пусть фазовая модуляция осуществляется двух тоновым сигналом, в котором одна частота (Ω1) очень низкая, а вторая (Ω2) во много раз выше первой. Поскольку при ФМ индекс модуляции не зависит от модулирующей частоты, спектры для обеих модулирующих частот будут подобны (см. рис. 8.4а).
Предположим теперь, что при частотной модуляции на нижней частоте Ω1 индекс модуляции такой же, как при
ФМ. Тогда на верхней частоте, согласно (8.11), индекс модуляции будет во много раз меньше, и, следовательно, эффективная полоса, при частоте модуляции Ω2,значительно сократится. Спектр сигнала с ЧМ для этого случая представлен на рисунке 8.4б.
Таким образом, при частотной модуляции реальным многочастотным сигналом, полоса модулированного сигнала (Пчм) оказывается значительно уже, по сравнению с полосой сигнала при фазовой модуляцией (Пфм). По этой причине, для целей радиосвязи и радиовещания предпочтение отдаётся частотной модуляции.
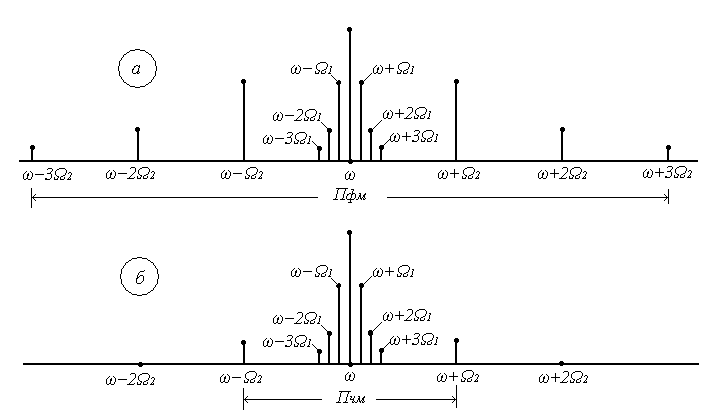
Рисунок 8.4 – Спектры сигналов с ФМ и ЧМ
8.3 Методы получения частотной модуляции
Колебания с частотной модуляцией можно получить, либо непосредственно, изменяя частоту колебаний автогенератора, либо путём преобразования фазовой модуляции в частотную. Метод непосредственного изменения частоты получил название «прямого» метода ЧМ, соответственно преобразование ФМ в ЧМ называют «косвенным» методом.
Прямые методы ЧМ основаны на изменении реактивности колебательной системы автогенератора под воздействием модулирующего сигнала.
При косвенных методах фазовую модуляцию получают при прохождении несущего колебания через цепь, сдвиг фазы в которой зависит от модулирующего сигнала. Преобразование ФМ в ЧМ обеспечивается коррекцией модулирующего сигнала интегрирующей RC– цепью (см. п.п. 8.1).
8.3.1 Прямые методы ЧМ
Для изменения частоты автогенератора в его колебательную систему включается управляемая реактивность. В качестве такой реактивности в настоящее время, как правило, используются ёмкость запертого p-n перехода специального полупроводникового диода – варикапа. В первом приближении ёмкость перехода может быть описана следующим выражением
Здесь е -запирающее напряжение на варикапе; Со – ёмкость варикапа при е = 0; φк = 0,3 ÷ 0,5 В - контактная разность потенциалов; n- показатель «резкости» перехода, который может принимать значения от 0,3 до 3.
Значение n = 0,3 соответствует «плавному» переходу; n = 0,5 – «резкому»; n ≥ 1
– «сверх резкому» переходу. Графики, соответствующие (9.15) приведены на рисунке 8.5б.
Схема автогенератора с частотной модуляцией (без цепей питания) представлена на рисунке 8.5а
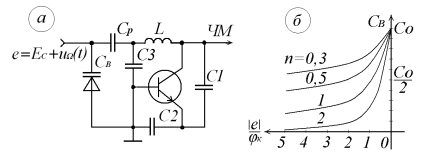
Рисунок 8.5 - Схема ЧМ автогенератора с варикапом
Обычно ёмкости схемы автогенератора подбираются так, чтобы
С3<<C1,C2 и СВ>C3. При этих условиях ёмкость контура в основном определяется ёмкостью варикапа Ск ≈ СВ . Резонансную частоту контура в этом случае можно определить следующим выражением
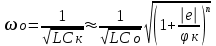 (8.16)
(8.16)Совершенно очевидно, что пропорциональная зависимость между резонансной частотой контура ωο и напряжением на переходе е (а значит и частотой генерируемых колебаний ω) возможна только при n = 2.
В процессе модуляции
е= Ес+иΩ(t)+ u(t)= Ес+UΩcosΩt + Ucosωt (8.17)
Здесь Ес – напряжение смещения на варикапе; иΩ(t)- модулирующий сигнал; u(t)- колебания высокой частоты, поступающие на варикап со стороны автогенератора.
Поскольку переход должен быть в закрытом состоянии (e<0), необходимо выполнить условие
UΩ+ U≤ |Ec| (8.18)
Полагая в (8.16) n=2, с учётом (8.17),для частоты генерируемых колебаний получим
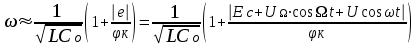 (8.19)
(8.19)Таким образом, для линейной частотной модуляции желательно иметь варикап со сверх резким переходом. На практике промышленные образцы
варикапов обычно имеют резкие переходы с n ≈0,5. Поэтому приходится ограничивать величину девиации частоты. Для получения необходимой девиации, первичную модуляцию осуществляют на пониженной частоте, а затем с помощью умножителя переносят ЧМ колебание на рабочую частоту. При этом девиация частоты увеличивается в соответствии с кратностью умножения.
Меньшие искажения при большей девиации могут быть получены с помощью «реактивного транзистора» (реактивной лампы) [12]. Реактивный транзистор представляет собой, как и варикап, управляемую реактивность (Хр)ёмкостного или индуктивного характера, подключаемую к контуру автогенератора. Схема реактивного транзистора представлена на рисунке 8.6а.