Файл: Методические указания для студентов всех форм обучения для всех.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 52
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации Уральский федеральный университет
имени первого Президента России Б.Н. Ельцина
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ В ЛАБОРАТОРИЯХ ФИЗИЧЕСКОГО ПРАКТИКУМА
Методические указания для студентов всех форм обучения для всех специальностей
1
Екатеринбург УрФУ 2010
УДК 53.082.07
Составители: В.А. Овчинников, Ю.Г. Карпов, А.А. Повзнер Научный редактор проф., д-р физ.- мат. наук Ф.А. Сидоренко
Математическая обработка результатов измерений в лабораториях физического практикума: методические указания / сост. В.А. Овчинников, Ю.Г. Карпов, А.А. Повзнер. Екатеринбург: УрФУ, 2010. 20 c.
В работе приведена классификация погрешностей результатов измерений, изложены основы статистического метода оценки доверительных границ случайных и систематических погрешностей, даны практические рекомендации по математической обработке экспериментальных результатов лабораторных работ физического практикума. Приведены примеры обработки результатов измерений. Предназначено для студентов всех специальностей всех форм обучения.
Подготовлено кафедрой физики
2
УрФУ, 2010
Принятые обозначения
Х– случайная физическая величина (её обозначение);
х0 –истинное значение физической величины Х;
х1, х2,……, хn – случайные значения измеряемой физической величины Х; n–число результатов наблюдений;
х – среднее арифметическое значение физической величины Х; Р– вероятность;
Sx– среднее квадратическое отклонение среднего арифметического;
tp,n– коэффициент Стьюдента;
ε – доверительная граница случайной погрешности результата измерения; θ – доверительная граница неисключённой систематической погрешности
результата измерения;
Δ – доверительная граница абсолютной погрешности результата измерения; γ – доверительная граница относительной погрешности результата
измерения
3-
Измерения физических величин. Погрешности измерений
Измерениефизической величины – это нахождение значения физической величины опытным путем с помощью специальных технических средств – приборов, установок и т. д.
По способу получения значения измеряемой величины различают прямые и косвенные измерения.
Прямоеизмерение– измерение, при котором искомое значение величины получают непосредственно из опытных данных. Например, прямыми являются измерения массы с помощью весов, длины с помощью линейки и т.д.
Косвенноеизмерение– измерение, при котором искомое значение величины находят вычислением на основании известной зависимости между этой величиной и величинами,
определяемыми в результате прямых измерений. Так, при определении плотности тела правильной формы проводят прямые измерения его массы, размеров, а затем уже рассчитывают плотность.
Например, для тела цилиндрической формы плотность р рассчитывается по формуле
2
p = 4???? ,
???? ℎ
где т– масса цилиндра, d– диаметр, h– высота.
Величины d,mи hопределяют в результате прямых измерений.
В силу ряда причин результат измерения любой физической величины не совпадает с ее истинным значением. Отклонение результата измерения от истинного значения измеряемой величины называется погрешностьюизмерения.Задачей любого измерения является не только установление наиболее точного значения измеряемой величины, но и оценка границ возможных погрешностей.
По форме представления различают абсолютные и относительные
погрешности.
АбсолютнаяпогрешностьΔ0 – разность между измеренным хи х0
истинным значениями измеряемой величины;
Δ0 = х–х0 (1)
Относительная погрешность γ0 - отношение абсолютной погрешности к истинному значению х0 измеряемой величины:
γ0 = 0
????0
– в относительных единицах
или γ0 = 0 100 % – в процентах.
????0
Поскольку истинное значение измеряемой величины остается неизвестным, на практике можно найти лишь приближенную оценку погрешности.
По причинам возникновения различают следующие основные виды погрешностей:
метода измерений (обусловлены несовершенством метода измерений), средств измерений (обусловлены техническими недостатками средств измерений),
отсчитывания(обусловлены округлением показаний средств измерений).
По характеру изменения при повторных измерениях погрешность любого измерения складывается из двух составляющих – случайной и систематической.
Пусть мы измерили какую-либо физическую величин X несколько раз. Как показывает опыт, полученные результаты будут между собой несколько различаться. Это различие обусловлено тем, что условия измерений и сам объект измерения с течением времени случайным, неконтролируемым образом изменяются. Поэтому считают, что различие результатов наблюдений обусловлено случайными погрешностями.
Случайнаяпогрешность– составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях данной
величины.
Систематическаяпогрешность– составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях данной величины.
-
Оценка границ случайной погрешности прямого измерения Пусть в некоторой серии опытов получены пзначений физической величины X:х1, х2 , хn. Каждое отдельное измерение называют наблюдением;
значения х1,х2.... ,хn– результатаминаблюдений. Если считать, что систематические погрешности отсутствуют, то, как показывает теория вероятностей, наиболее близким к неизвестному истинному значению х0этой величины является среднееарифметическоеэтих значений.
х= хх2 х(2)
????
Можно ожидать (и это доказывается методами математической статистики), что при увеличении числа наблюдений псреднее арифметическое хдолжно приближаться к истинному значению x0 измеряемой величины, т.е.
lim????→∞ ???? = x0
Итак, для того чтобы определить истинное значение измеряемой физической величины X,необходимо провести бесконечное число ее наблюдений и найти среднее арифметическое полученных результатов. Это невыполнимая задача. В любом реальном эксперименте число наблюдений конечно, поэтому среднее арифметическое их результатов отличается от истинного значения. Задача исследователя - оценить для данной совокупности наблюдений возможные отклонения х от х0. Это делается с применением математического аппарата теории вероятностей. Познакомимся с некоторыми ее понятиями.
При проведении большой серии наблюдений некоторой величины X
чаще всего встречаются результаты, довольно близкие к ее истинному
значению х0. Чем больше случайное значение х отличается от истинного х0,тем реже оно встречается. Выделим среди возможных результатов наблюдений некоторый интервал Δх, Пусть из п проведенных наблюдений Δп дали результаты, лежащие в этом интервале. Вероятность попадания результата наблюдения хв интервал Δхопределяется выражением
P lim n.
n n
Если данная величина X непрерывна, то существует отличная от нуля вероятность dРпопадания результата отдельного наблюдения в любой элементарный интервал dх.Эта вероятность в общем случае зависит от ширины интервала dxи от того, в окрестности какого значения хвыбран этот интервал, т.е.
dР=f(х)dx.
Функция f(x)называется плотностьювероятности,или плотностьюфункциираспределенияслучайной величины X.
Очень часто при измерениях физических величин распределение результатов наблюдений подчиняется так называемому нормальному, или гауссовузакону
f(x)=
1 e
√2????
−(????−????0)2
2????2 (3)
График этой зависимости представлен на рисунке.
Параметр σ2 называется дисперсией распределения, а σ – средним квадратическим отклонением. Этот параметр характеризует разброс значений измеряемой величины относительно ее истинного значения х0: чем больше σ, тем больше этот разброс.
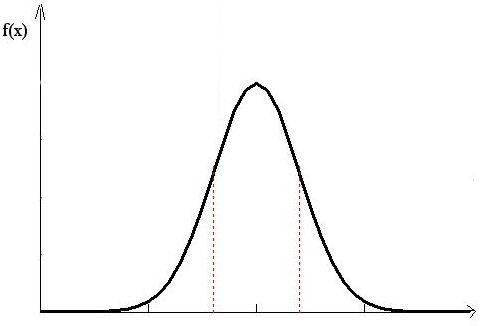
0 х0-σ х0 х0+σ x
В теории вероятностей доказывается, что если будет проведена беско- нечно большая серия наблюдений величины X и если результаты будут рас- пределены по нормальному закону, то вероятность того, что результат хкаждого отдельного наблюдения попадает в интервал от х0 – σ до х0 + σ или того, что случайная погрешность не превысит значения ± σ, равна Р = 0,6827 Вероятности попадания результатов наблюдений в более широкие интервалы х0 ±2σ и х0 ± Зσ равны соответственно 0,9545 и 0,9975. Случайные погрешности в этих случаях с вероятностью 0,9545 и 0,9975 не превышают значений ±2σ и ±3σ .
Вероятность попадания результатов наблюдений в заданный интервал значений называется доверительнойвероятностью,сам интервал – доверительныминтервалом,границы погрешностей – доверительнымиграницамипогрешностей.Так, в первом из рассмотренных примеров доверительный интервал равен х0 ±σ, доверительная вероятность Р= 0,6827.
Для нахождения σ необходимо провести бесконечно большое число наблюдений и построить f(х).В реальных условиях число наблюдений конечно, поэтому можно найти лишь приближенную оценку σ. Эта оценка называется выборочным средним квадратическим отклонением SХрезультата отдельного наблюдения и вычисляется по формуле
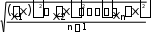Sx
(4)
где х – среднее арифметическое значение величины Xдля данной выборки (конечной серии) наблюдений.
Таким образом, проведя конечную серию наблюдений и определив среднее квадратическое отклонение, можно для любого из результатов наблюдений указать с определенной вероятностью доверительный интервал значений и доверительные границы случайной погрешности.
Однако обычно важнее оценить границы случайной погрешности не результата каждого отдельного наблюдения, а их среднего арифметического
x , которое принято называть результатомизмеренияфизическойвеличиныX.Среднее арифметическое xтакже является случайной величиной. Если случайные значения распределены по нормальному закону,
то но такому же закону распределены и средние арифметические значения x.
Теория показывает, что отклонение среднего арифметического x от истинного значения х0характеризуется не величиной Sx, а меньшей величиной Sx,
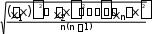называемой средним квадратическим отклонением среднего арифметического:
Sx
(5)
Определив для данной серии наблюдений xи Sxможно записать окончательный результат в виде
Х=x±2σ, Р= 0,95
т.е. с вероятностью Р= 0,95 найденное значение xне отличается от истинного
х0более чем на ±2σ.
Различие между Sxи xневелико, а распределение результатов
измерений мало отличается от нормального только при достаточно больших
значениях п(п>30). В учебных лабораториях, как правило, ограничиваются
небольшим числом наблюдений (3 – 5). В этом случае Sxи xразличаются
сильно, поэтому для правильной оценки доверительных границ случайной погрешности вместо целочисленных коэффициентов при Sxвводятся
превышающие их дробные коэффициентыСтьюдента.
Оперируя методами теории вероятностей, английский математик Госсет в вышедшей в 1908 г. под псевдонимом "Стьюдент" работе показал, что в
случае небольшого числа наблюдений доверительная граница x
случайной
погрешности среднего арифметического оценивается по формуле
x tP,nSx,
(6)
где tP,nкоэффициент Стьюдента, зависящий от принятой доверительной вероятности Ри числа наблюдений п;
Sx– среднее квадратическое отклонение среднего арифметического. Значения коэффициентов Стьюдента для доверительной вероятности Р0,95 (в учебных лабораториях рекомендуется определять доверительные границы погрешности именно для такой вероятности) приведены в таблице:
n
2
3
4
5
6
7
8
9
10
t0,95; n
12,7
4,3
3,18
2,77
2,57
2,45
2,36
2,31
2,26
-
Оценка границ неисключенной систематической погрешности прямого измерения
В некоторых случаях модуль и знак систематической погрешности известны. Такая погрешность должна быть исключена путем введения соответствующей поправки. Так, если известно, что секундомер отстает на 1с в течение часа, то к его показаниям следует добавлять поправку из расчета 1с на каждый час времени.
10
Однако имеются такие систематические погрешности, модуль и знак которых неизвестны. Такие погрешности называются неисключенными и
должны быть учтены.
В паспорте средства измерения, как правило, указывается пределосновной погрешности (кратко – основная погрешность), т.е. погрешность, которая может возникнуть при использовании этого средства в нормальных условиях (при рекомендуемых температурах, влажности и т.д.). Например, если в паспорте микрометра указано, что предел основной погрешности составляет ±0,004 мм, то это означает, что при измерении линейных размеров какого-либо тела без нарушений правил измерения и в соответствующих условиях основная систематическая погрешность измерения не превышает
±0,004 мм.
Часто предел основной погрешности средства измерения задается классом точности, Класс точности δ средства измерения показывает, сколько процентов от его верхнего предела измерений хmax(или номинального значения xном) составляет предел основной погрешности этого средства:
осн 100%.
хmax
Электроизмерительные приборы могут иметь следующие классы точности: 0,05;0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности прибора обычно указывается на шкале прибора. Для виртуальных измерительных приборов класс точности принимается равным 1,0.
Предел основной погрешности прибора одинаков во всем его диапазоне измерений, возможная относительная погрешность зависит от показания прибора. Например, миллиамперметром на Imax = 100 мА измерена сила тока /
I
= 20 мА. Класс точности прибора δ = 1,0. Предел основной погрешности составляет
осн
100мА1% 1мА
max 100% 100%
возможная относительная основная погрешность указанного в примере показания не превышает
осн 1мА
0, 05 5%.
I 20мА
Наряду с основной погрешностью средства измерений в систематическую погрешность измерения входит также погрешностьотсчитывания θотсч., равная половине цены наименьшего давления шкалы, если отсчет показаний ведется с точностью до целых делений. Погрешность отсчитывания является систематической погрешностью только при однократных измерениях; при многократных измерениях она становится составляющей случайной погрешности, поскольку показания средства измерения в этом случае округляются как в сторону завышения, так и в сторону занижения результатов наблюдений.
Как уже отмечалось, систематическая погрешность может возникнуть и из-за несовершенства метода измерений и по целому ряду других причин. Единого рецепта для оценки погрешности метода и других составляющих систематической погрешности не существует. Обычно они могут быть оценены теоретически или определены в специальных градуировочных опытах.
Итак, составляющими систематической погрешности являются: предел основной погрешности средства измерений θосн.; погрешность отсчитывания θотсч; погрешность метода θм; погрешности, вызванные другими источниками (изменение температуры окружающей среды, изменение влажности и т.д.). При оценке доверительной границы неисключенной систематической погрешности θХпри п = 1 следует учитывать основную погрешность средства измерений θосн и погрешность отсчитывания θотсч. ; в случае п>1 только θосн. Погрешность метода θм мы будем учитывать лишь в том случае, если она существенна и задана в описании к лабораторной работе.
Для оценки θХтакже используется теория вероятностей. Согласно этой теории доверительная граница неисключенной систематической погрешности результата измерения при Р= 0,95 оценивается по формуле
x
осн отсч м
2
2
2 ....
(7)
-
Оценка границ погрешности результата прямого измерения После того, как определены доверительные границы случайной и систематической погрешностей, необходимо оценить границы
полной
погрешности результата измерений. Для этого прежде всего сравнивают доверительную границу θХ систематической погрешности и среднее
квадратическое отклонение Sxрезультата измерений.
x
-
В случае, если Sx< 0,8, систематической погрешностью по
сравнению со случайной пренебрегают и принимают, что граница погрешности результата Δx = εx,
x
-
Если Sx>8,0, то случайной погрешностью по сравнению с систематичес-
кой пренебрегают и принимают , что граница результата Δx = θx,
x
-
Если ни одно из этих неравенств не выполняется, т.е. 0,8 < Sx
< 8,0, то
необходимо учитывать обе составляющие погрешности измерения, В этом случае доверительную границу погрешности результата оценивают по формуле
2 2 .
(8)
x x x
После того, как граница погрешности результата измерений Ах
определена, окончательный результат записывают в виде
Х=x x,Р = 0,95.
Величины xи Δx должны быть согласованы по точности: они должны содержать последнюю значащую цифру в одном и том же разряде. Если, например, x = 64,538 мм и Δx = 0,028 мм, необходимо округлить Δx до первой значащей цифры: Δx = 0,03 мм, а затем и xокруглить до цифры того десятичного разряда, которым выражена погрешность: x= 64,54 мм. Окончательный результат измерения записывают в виде
Х=(64,54 ± 0,03) мм, Р– 0,95.
-
1 2 3 4 5
2
p = 4???? ,
γ0 = 0
????0
– в относительных единицах
или γ0 = 0 100 % – в процентах.????0
Поскольку истинное значение измеряемой величины остается неизвестным, на практике можно найти лишь приближенную оценку погрешности.
По причинам возникновения различают следующие основные виды погрешностей:
метода измерений (обусловлены несовершенством метода измерений), средств измерений (обусловлены техническими недостатками средств измерений),
отсчитывания(обусловлены округлением показаний средств измерений).
По характеру изменения при повторных измерениях погрешность любого измерения складывается из двух составляющих – случайной и систематической.
Пусть мы измерили какую-либо физическую величин X несколько раз. Как показывает опыт, полученные результаты будут между собой несколько различаться. Это различие обусловлено тем, что условия измерений и сам объект измерения с течением времени случайным, неконтролируемым образом изменяются. Поэтому считают, что различие результатов наблюдений обусловлено случайными погрешностями.
Случайнаяпогрешность– составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях данной
Оценка границ случайной погрешности прямого измерения Пусть в некоторой серии опытов получены пзначений физической величины X:х1, х2 , хn. Каждое отдельное измерение называют наблюдением;
f(x)=
1 e
√2???? −(????−????0)2
2????2 (3)График этой зависимости представлен на рисунке.
Параметр σ2 называется дисперсией распределения, а σ – средним квадратическим отклонением. Этот параметр характеризует разброс значений измеряемой величины относительно ее истинного значения х0: чем больше σ, тем больше этот разброс.
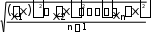Sx(4)
где х – среднее арифметическое значение величины Xдля данной выборки (конечной серии) наблюдений.
Таким образом, проведя конечную серию наблюдений и определив среднее квадратическое отклонение, можно для любого из результатов наблюдений указать с определенной вероятностью доверительный интервал значений и доверительные границы случайной погрешности.
Однако обычно важнее оценить границы случайной погрешности не результата каждого отдельного наблюдения, а их среднего арифметического
x , которое принято называть результатомизмеренияфизическойвеличиныX.Среднее арифметическое xтакже является случайной величиной. Если случайные значения распределены по нормальному закону,
то но такому же закону распределены и средние арифметические значения x.
Теория показывает, что отклонение среднего арифметического x от истинного значения х0характеризуется не величиной Sx, а меньшей величиной Sx,
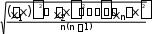называемой средним квадратическим отклонением среднего арифметического:
Sx
(5)
Определив для данной серии наблюдений xи Sxможно записать окончательный результат в видеХ=x±2σ, Р= 0,95
т.е. с вероятностью Р= 0,95 найденное значение xне отличается от истинного
х0более чем на ±2σ.
Различие между Sxи xневелико, а распределение результатов
случае небольшого числа наблюдений доверительная граница x
случайной
погрешности среднего арифметического оценивается по формуле
x tP,nSx,
(6)
где tP,nкоэффициент Стьюдента, зависящий от принятой доверительной вероятности Ри числа наблюдений п;
Sx– среднее квадратическое отклонение среднего арифметического. Значения коэффициентов Стьюдента для доверительной вероятности Р0,95 (в учебных лабораториях рекомендуется определять доверительные границы погрешности именно для такой вероятности) приведены в таблице:
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| t0,95; n | 12,7 | 4,3 | 3,18 | 2,77 | 2,57 | 2,45 | 2,36 | 2,31 | 2,26 |
-
Оценка границ неисключенной систематической погрешности прямого измерения
В некоторых случаях модуль и знак систематической погрешности известны. Такая погрешность должна быть исключена путем введения соответствующей поправки. Так, если известно, что секундомер отстает на 1с в течение часа, то к его показаниям следует добавлять поправку из расчета 1с на каждый час времени.
10
Однако имеются такие систематические погрешности, модуль и знак которых неизвестны. Такие погрешности называются неисключенными и осн
100мА1% 1мА
max 100% 100%
возможная относительная основная погрешность указанного в примере показания не превышает
осн 1мА
0, 05 5%.
I 20мА
Наряду с основной погрешностью средства измерений в систематическую погрешность измерения входит также погрешностьотсчитывания θотсч., равная половине цены наименьшего давления шкалы, если отсчет показаний ведется с точностью до целых делений. Погрешность отсчитывания является систематической погрешностью только при однократных измерениях; при многократных измерениях она становится составляющей случайной погрешности, поскольку показания средства измерения в этом случае округляются как в сторону завышения, так и в сторону занижения результатов наблюдений.
Как уже отмечалось, систематическая погрешность может возникнуть и из-за несовершенства метода измерений и по целому ряду других причин. Единого рецепта для оценки погрешности метода и других составляющих систематической погрешности не существует. Обычно они могут быть оценены теоретически или определены в специальных градуировочных опытах.
Итак, составляющими систематической погрешности являются: предел основной погрешности средства измерений θосн.; погрешность отсчитывания θотсч; погрешность метода θм; погрешности, вызванные другими источниками (изменение температуры окружающей среды, изменение влажности и т.д.). При оценке доверительной границы неисключенной систематической погрешности θХпри п = 1 следует учитывать основную погрешность средства измерений θосн и погрешность отсчитывания θотсч. ; в случае п>1 только θосн. Погрешность метода θм мы будем учитывать лишь в том случае, если она существенна и задана в описании к лабораторной работе.
Для оценки θХтакже используется теория вероятностей. Согласно этой теории доверительная граница неисключенной систематической погрешности результата измерения при Р= 0,95 оценивается по формуле
x
осн отсч м
2 2
2 ....
(7)
Оценка границ погрешности результата прямого измерения После того, как определены доверительные границы случайной и систематической погрешностей, необходимо оценить границы
В случае, если Sx< 0,8, систематической погрешностью по
Если Sx>8,0, то случайной погрешностью по сравнению с систематичес-
x
-
Если ни одно из этих неравенств не выполняется, т.е. 0,8 < Sx
< 8,0, то
необходимо учитывать обе составляющие погрешности измерения, В этом случае доверительную границу погрешности результата оценивают по формуле
2 2 .(8)
x x x
После того, как граница погрешности результата измерений Ах
определена, окончательный результат записывают в виде
Х=x x,Р = 0,95.
Величины xи Δx должны быть согласованы по точности: они должны содержать последнюю значащую цифру в одном и том же разряде. Если, например, x = 64,538 мм и Δx = 0,028 мм, необходимо округлить Δx до первой значащей цифры: Δx = 0,03 мм, а затем и xокруглить до цифры того десятичного разряда, которым выражена погрешность: x= 64,54 мм. Окончательный результат измерения записывают в виде
- 1 2 3 4 5
Оценка границ погрешности косвенного измерения
При косвенном измерении значение искомой величины Y находят по результатам прямых измерений величин Х1,Х2,..,Хт,которые связаны с Yизвестной зависимостью
Y=f(X1,X2,…,Xm) (9)
Проведя серии прямых наблюдений величин X1, Х2, ... , Хт, можно
найти их оценки, т.е. средние арифметические
x1, x2,...., xm, а также определить
доверительные границы погрешностей результатов их измерений: ΔХ1,ΔХ2
,...,ΔХт– Наиболее вероятным значением Yследует считать y , которое получается, если в формулу (9) подставить средние значения аргументов Х1, Х2 ..., Хт.
Y= y= f(x1, x2,...., xm) (10)
Теория вероятностей показывает, что когда погрешности измеряемых аргументов не зависят друг от друга, доверительная граница относительной погрешности уизмерения величины Yоценивается по формуле
y
y
f
, (11)
где –
x1
частная производная функции fпо аргументу x1;