Файл: Арзамасский государственный педагогический институт имени А. П. Гайдара Кафедра математического анализа.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
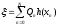 , где
, где 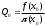 ,
, 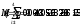 . Если
. Если 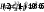 при
при 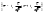 , и
, и 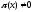 при
при 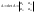 , то при некотором дополнительном условии
, то при некотором дополнительном условии 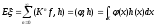 . Важность достижения малой дисперсии в знакопостоянном случае показывает следующее утверждение: если
. Важность достижения малой дисперсии в знакопостоянном случае показывает следующее утверждение: если 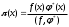 и
и 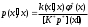 , где
, где 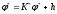 , то
, то 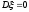 , а
, а 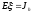 . Моделируя подходящую цепь Маркова на ЭВМ, получают статистическую оценку линейных функционалов от решения интегрального уравнения второго рода. Это даёт возможность и локальной оценки решения на основе представления:
. Моделируя подходящую цепь Маркова на ЭВМ, получают статистическую оценку линейных функционалов от решения интегрального уравнения второго рода. Это даёт возможность и локальной оценки решения на основе представления: 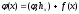 , где
, где 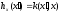 . Методом Монте-Карло оценка первого собственного значения интегрального оператора осуществляется интерациональным методом на основе соотношения
. Методом Монте-Карло оценка первого собственного значения интегрального оператора осуществляется интерациональным методом на основе соотношения 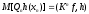 . Все рассмотренные результаты почти автоматически распространяются на системы линейных алгебраических уравнений вида
. Все рассмотренные результаты почти автоматически распространяются на системы линейных алгебраических уравнений вида 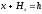 . Решение дифференциальных уравнений осуществляется методом Монте-Карло на базе соответствующих интегральных соотношений.
. Решение дифференциальных уравнений осуществляется методом Монте-Карло на базе соответствующих интегральных соотношений.§2. Способ усреднения подынтегральной функции.
В качестве оценки определённого интеграла
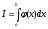 принимают
принимают 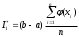 ,
,где n – число испытаний;
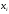 - возможные значения случайной величины X, распределённой равномерно в интервале интегрирования
- возможные значения случайной величины X, распределённой равномерно в интервале интегрирования 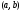 , их разыгрывают по формуле
, их разыгрывают по формуле 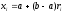 , где
, где 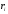 - случайное число.
- случайное число.Дисперсия усредняемой функции
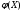
равна
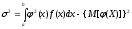 ,
,где
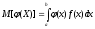 ,
, 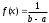 . Если точное значение дисперсии вычислить трудно или невозможно, то находят выборочную дисперсию (при n>30)
. Если точное значение дисперсии вычислить трудно или невозможно, то находят выборочную дисперсию (при n>30) 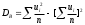 , или исправленную дисперсию (при n<30)
, или исправленную дисперсию (при n<30) 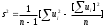 , где
, где 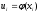 .
. Эти формулы для вычисления дисперсии применяют и при других способах интегрирования, когда усредняемая функция не совпадает с подынтегральной функцией.
В качестве оценки интеграла
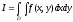 , где область интегрирования D принадлежит единичному квадрату
, где область интегрирования D принадлежит единичному квадрату 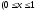 ,
, 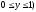 , принимают
, принимают 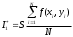 , (*)
, (*)где S – площадь области интегрирования; N – число случайных точек
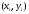 , принадлежащих области интегрирования.
, принадлежащих области интегрирования. Если вычислить площадь S трудно, то в качестве её оценки можно принять
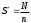 ; в этом случае формула (*) имеет вид
; в этом случае формула (*) имеет вид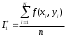 ,
,где n – число испытаний.
В качестве оценки интеграла
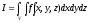 , где область интегрирования V принадлежит единичному кубу
, где область интегрирования V принадлежит единичному кубу 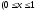 ,
, 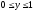 ,
, 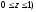 , принимают
, принимают 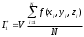 , где V – объём области интегрирования, N – число случайных точек
, где V – объём области интегрирования, N – число случайных точек 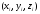 , принадлежащих области интегрирования.
, принадлежащих области интегрирования. Если вычислить объём трудно, то в качестве его оценки можно принять
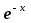 , в этом случае формула (**) имеет вид
, в этом случае формула (**) имеет вид 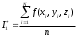 , где n – число испытаний.
, где n – число испытаний.Задача: найти оценку
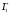 определённого интеграла
определённого интеграла 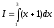 .
.Решение. Используем формулу
 . По условию, a=1, b=3,
. По условию, a=1, b=3, 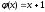
. Примем для простоты число испытаний n=10.Тогда оценка
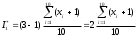 , где возможные значения
, где возможные значения  разыгрывается по формуле
разыгрывается по формуле 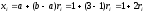 .
.Результаты десяти испытаний приведены в таблице 1.
Случайные числа
 взяты из таблицы приложения.
взяты из таблицы приложения.Таблица 1.
| Номер i | | | |
| 1 2 3 4 5 6 7 8 9 10 | 0,100 0,973 0,253 0,376 0,520 0,135 0,863 0,467 0,354 0,876 | 1,200 2,946 1,506 1,752 2,040 1,270 2,726 1,934 1,708 2,752 | 2,200 3,946 2,506 2,752 3,040 2,270 3,726 2,934 2,708 3,752 |
Из таблицы 1 находим
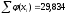 . Искомая оценка
. Искомая оценка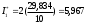
§3. Способ существенной выборки, использующий «вспомогательную плотность распределения».
В качестве оценки интеграла
 принимают
принимают 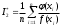 , где n – число испытаний; f(x) – плотность распределения «вспомогательной» случайной величины X, причём
, где n – число испытаний; f(x) – плотность распределения «вспомогательной» случайной величины X, причём 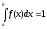 ;
;  - возможные значения X, которые разыгрывают по формуле
- возможные значения X, которые разыгрывают по формуле 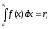 .
.Функцию f(x) желательно выбирать так, чтобы отношение
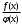 при различных значениях x изменялось незначительно. В частности, если
при различных значениях x изменялось незначительно. В частности, если  , то получим оценку
, то получим оценку 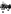 .
.Задача. Найти оценку
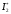 интеграла
интеграла 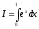
.
Решение. Так как
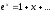 , то в качестве плотности распределения «вспомогательной» случайной величины X примем функцию
, то в качестве плотности распределения «вспомогательной» случайной величины X примем функцию 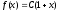 . Из условия
. Из условия 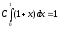 найдём
найдём 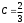 . Итак,
. Итак, 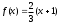 .
.Запишем искомый интеграл так:
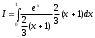 .
.Таким образом, интеграл I представлен в виде математического ожидания функции
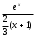 . В качестве искомой оценки примем выборочную среднюю (для простоты ограничимся десятью испытаниями):
. В качестве искомой оценки примем выборочную среднюю (для простоты ограничимся десятью испытаниями):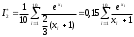 ,
, где
 - возможные значения X, которые надо разыграть по известной плотности
- возможные значения X, которые надо разыграть по известной плотности 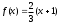 . По правилу (для того, чтобы разыграть возможное значение
. По правилу (для того, чтобы разыграть возможное значение  непрерывной случайной величины X, зная её плотность вероятности f(x), надо выбрать случайное число
непрерывной случайной величины X, зная её плотность вероятности f(x), надо выбрать случайное число  и решить относительно
и решить относительно  уравнение
уравнение 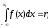 , или уравнение
, или уравнение 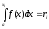 ,
, где a – наименьшее конечно возможное значение X), имеем
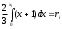 . Отсюда находим явную формулу для разыгрывания возможных значений X:
. Отсюда находим явную формулу для разыгрывания возможных значений X: 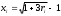 .
.В таблице 2 приведены результаты 10 испытаний.
Сложив числа последней строки таблицы 2, получим
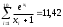 . Искомая оценка равна
. Искомая оценка равна 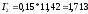 .
. Таблица 2.
| Номер i | | | | | |
| 1 2 3 4 5 6 7 8 9 10 | 0,100 0,973 0,253 0,376 0,520 0,135 0,863 0,467 0,354 0,876 | 0,140 0,980 0,326 0,459 0,600 0,185 0,894 0,550 0,436 0,905 | 1,150 2,664 1,385 1,582 1,822 1,203 2,445 1,733 1,546 2,472 | 1,140 1,980 1,326 1,459 1,600 1,185 1,894 1,550 1,436 1,905 | 1,009 1,345 1,044 1,084 1,139 1,015 1,291 1,118 1,077 1,298 |
§4. Способ, основанный на истолковании интеграла как площади.
Пусть подынтегральная функция неотрицательна и ограничена:
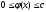 , а двумерная случайная величина
, а двумерная случайная величина 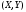 распределена равномерно в прямоугольнике D с основанием
распределена равномерно в прямоугольнике D с основанием 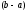 и высотой
и высотой  . Тогда двумерная плотность вероятности
. Тогда двумерная плотность вероятности 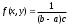 для точек, принадлежащих D;
для точек, принадлежащих D; 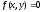 вне D.
вне D.В качестве оценки интеграла
 принимают
принимают 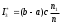 , где n – общее число случайных точек
, где n – общее число случайных точек  , принадлежащих D;
, принадлежащих D; 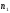 - число случайных точек, которые расположены под кривой
- число случайных точек, которые расположены под кривой 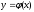 .
.Задача. Найти оценку
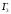 интеграла
интеграла 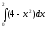 .
.Решение. Используем формулу
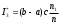 .
.В интервале (0,2) подынтегральная функция
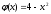 неотрицательна и ограничена, причём
неотрицательна и ограничена, причём 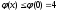 ; следовательно, можно принять c=4.
; следовательно, можно принять c=4.Введём в рассмотрение двумерную случайную величину (X,Y), распределённую равномерно в прямоугольнике D с основанием
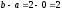 и высотой с=4, плотность вероятности которой
и высотой с=4, плотность вероятности которой 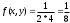 .
. Разыгрываем n=10 случайных точек
 , принадлежащих прямоугольнику D. Учитывая, что составляющая X в интервале (0,2) распределена равномерно с плотностью
, принадлежащих прямоугольнику D. Учитывая, что составляющая X в интервале (0,2) распределена равномерно с плотностью 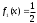 и составляющая Y в интервале (0,4) распределена равномерно с плотностью
и составляющая Y в интервале (0,4) распределена равномерно с плотностью 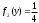 , разыграем координаты случайной точки
, разыграем координаты случайной точки  , принадлежащей прямоугольнику D, по паре независимых случайных чисел
, принадлежащей прямоугольнику D, по паре независимых случайных чисел 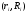 :
: