Файл: Арзамасский государственный педагогический институт имени А. П. Гайдара Кафедра математического анализа.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 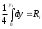 .Отсюда
.Отсюда 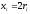 ,
, 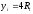 .
.
Если окажется, что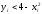 , то точка
, то точка  лежит под кривой
лежит под кривой  и в «счётчик
и в «счётчик 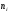 » надо добавить единицу.
» надо добавить единицу.
Результаты десяти испытаний приведены в таблице 3.
Из таблицы 3 находим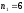 . Искомая оценка интеграла
. Искомая оценка интеграла
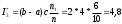
§5. Способ «выделения главной части».
В качестве оценки интеграла принимают
принимают
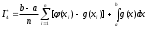 ,
,
где
- возможные значения случайной величины X, распределённой равномерно в интервале интегрирования , которые разыгрывают по формуле
, которые разыгрывают по формуле  ; функция
; функция 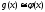 , причём интеграл
, причём интеграл 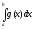 можно вычислить обычными методами.
можно вычислить обычными методами.
Задача. Найти оценку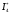 интеграла
интеграла 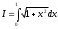 .
.
Решение. Так как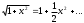
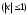 , то примем
, то примем 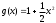 . Тогда, полагая число испытаний n=10, имеем оценку
. Тогда, полагая число испытаний n=10, имеем оценку
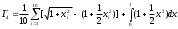 .
.
Выполнив элементарные преобразования, получим
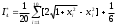 .
.
Учитывая, что a=0, b=1, возможные значения разыграем по формуле
разыграем по формуле 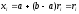 . Результаты вычислений приведены в таблице 4.
. Результаты вычислений приведены в таблице 4.
Сложив числа последнего столбца таблицы 4, найдём сумму 19,597, подставив которую в соотношение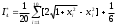
, получим искомую оценку интеграла
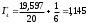 .
.
Заметим, что точное значение I=1,147.
§6. Программа вычисления определенного интеграла методом Монте-Карло.
Вычислить определенный интеграл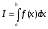 по методу “Монте-Карло” по формуле
по методу “Монте-Карло” по формуле
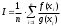 ,
,
где n – число испытаний ;g(x) – плотность распределения “вспомогательной” случайной величины X, причем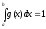 , в программе g(x) = 1/(b-a)
, в программе g(x) = 1/(b-a)
Программа написана на языке TURBO PASCAL 7.0
Program pmk;
Uses crt;
Var k,p,s,g,x,Integral : real;
n,i,a,b : integer;
BEGIN
writeln(‘Введите промежуток интегрирования (a;b):’);
readln(a);
readln(b);
writeln(‘Введите количество случайных значений(число испытаний):’);
readln(n);
k:=b-a; {Переменной“k”присвоим значение длины промежутка интегрирования}
writeln(‘k=’,k);
for i:= 1 to n do begin {проведем n испытаний}
g:=random; {g – переменная вещественного типа, случайная величина из промежутка [0;1]}
x:= a + g*(b-a); {По этой формуле получается произвольная величина из [a; b] }
s:=s + (1+x); {s:=s +(x*x)} {Вообще можно подставить любую функцию}
delay(1000); {задержка, чтобы произвольные значения не повторялись}
end; {конец испытаний}
writeln(‘s=’,s); {Сумма функции для n произвольных значений}
Integral:=(1/n)*k*s ;
writeln(‘Интеграл=’,Integral);
readln;
END.
Требуется ввести промежуток интегрирования и количество испытаний, интегрируемая функция уже задана в программе (но ее можно поменять).
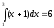 ;
; 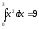 .
.
§7. Вычисление кратных интегралов методом Монте-Карло.
Пусть функция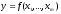
непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл

 . (1)
. (1)
Геометрически число I представляет собой (m+1)-мерный объём прямого цилиндроида в пространстве , построенного на основании S и ограниченного сверху данной поверхностью
, построенного на основании S и ограниченного сверху данной поверхностью  , где
, где  .
.
Преобразуем интеграл (1) так, чтобы новая область интегрирования целиком содержалась внутри единичного m-мерного куба. Пусть область S расположена в m-мерном параллелепипеде
 . (2)
. (2)
Сделаем замену переменных . (3)
. (3)
Тогда, очевидно, m-мерный параллелепипед (2) преобразуется в m-мерный единичный куб
 (4)
(4)
и, следовательно, новая область интегрирования σ, которая находится по обычным правилам, будет целиком расположена внутри этого куба.
Вычисляя якобиан преобразования, будем иметь:
 . Таким образом,
. Таким образом, 
 , (5)
, (5)
где . Введя обозначения
. Введя обозначения  и
и  , запишем интеграл (5) короче в следующем виде:
, запишем интеграл (5) короче в следующем виде: 
 . (5/)
. (5/)
Укажем способ вычисления интеграла (5/) методом случайных испытаний.
Выбираем m равномерно распределённых на отрезке [0, 1] последовательностей случайных чисел:

Точки можно рассматривать как случайные. Выбрав достаточно большое N число точек
можно рассматривать как случайные. Выбрав достаточно большое N число точек  , проверяем, какие из них принадлежат области σ (первая категория) и какие не принадлежат ей (вторая категория). Пусть
, проверяем, какие из них принадлежат области σ (первая категория) и какие не принадлежат ей (вторая категория). Пусть
1. при i=1, 2, …, n (6)
при i=1, 2, …, n (6)
2. при i=n+1, n+2, …,N (6/)
при i=n+1, n+2, …,N (6/)
(для удобства мы здесь изменяем нумерацию точек).
Заметим, что относительно границы Г области σ следует заранее договориться, причисляются ли граничные точки или часть их к области σ, или не причисляются к ней. В общем случае при гладкой границе Г это не имеет существенного значения; в отдельных случаях нужно решать вопрос с учётом конкретной обстановки.
Взяв достаточно большое число n точек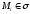 , приближённо можно положить:
, приближённо можно положить: 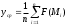 ; отсюда искомый интеграл выражается формулой
; отсюда искомый интеграл выражается формулой 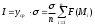 , где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять:
, где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять: 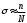 , отсюда
, отсюда 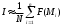 . В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто
. В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто 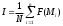 .
.
Заключение.
Метод Монте-Карло используется очень часто, порой некритично и неэффективным образом. Он имеет некоторые очевидные преимущества:
а) Он не требует никаких предложений о регулярности, за исключением квадратичной интегрируемости . Это может быть полезным, так как часто очень сложная функция, чьи свойства регулярности трудно установить.
б) Он приводит к выполнимой процедуре даже в многомерном случае, когда численное интегрирование неприменимо, например, при числе измерений, большим 10.
в) Его легко применять при малых ограничениях или без предварительного анализа задачи.
Он обладает, однако, некоторыми недостатками, а именно:
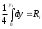 .Отсюда
.Отсюда 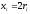 ,
, 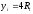 .
.| Номер i | | | | | | | |
| 1 2 3 4 5 6 7 8 9 10 | 0,100 0,253 0,520 0,863 0,354 0,809 0,911 0,542 0,056 0,474 | 0,200 0,506 1,040 1,726 0,708 1,618 1,822 1,084 0,112 0,948 | 0,040 0,256 1,082 2,979 0,501 2,618 3,320 1,175 0,013 0,899 | 3,960 3,744 2,918 1,021 3,499 1,382 0,680 2,825 3,987 3,101 | 0,973 0,376 ,135 0,467 0,876 0,590 0,737 0,048 0,489 0,296 | 3,892 1,504 0,540 1,868 3,504 2,360 2,948 0,192 1,956 1,184 | 1 1 1 1 1 1 |
Если окажется, что
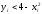 , то точка
, то точка  лежит под кривой
лежит под кривой  и в «счётчик
и в «счётчик 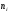 » надо добавить единицу.
» надо добавить единицу.Результаты десяти испытаний приведены в таблице 3.
Из таблицы 3 находим
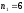 . Искомая оценка интеграла
. Искомая оценка интеграла 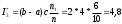
§5. Способ «выделения главной части».
В качестве оценки интеграла
 принимают
принимают 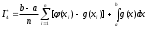 ,
, где

- возможные значения случайной величины X, распределённой равномерно в интервале интегрирования
 , которые разыгрывают по формуле
, которые разыгрывают по формуле  ; функция
; функция 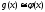 , причём интеграл
, причём интеграл 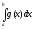 можно вычислить обычными методами.
можно вычислить обычными методами.Задача. Найти оценку
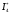 интеграла
интеграла 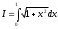 .
. Решение. Так как
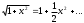
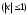 , то примем
, то примем 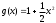 . Тогда, полагая число испытаний n=10, имеем оценку
. Тогда, полагая число испытаний n=10, имеем оценку 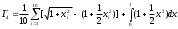 .
.Выполнив элементарные преобразования, получим
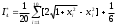 .
.Учитывая, что a=0, b=1, возможные значения
 разыграем по формуле
разыграем по формуле 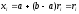 . Результаты вычислений приведены в таблице 4.
. Результаты вычислений приведены в таблице 4.| Номер i | | | | | |
| 1 2 3 4 5 6 7 8 9 10 | 0,100 0,973 0,253 0,376 0,520 0,135 0,863 0,467 0,354 0,876 | 0,010 0,947 0,064 0,141 0,270 0,018 0,745 0,218 0,125 0,767 | 1,010 1,947 1,064 1,141 1,270 1,018 1,745 1,218 1,125 1,767 | 1,005 1,395 1,032 1,068 1,127 1,009 1,321 1,104 1,061 1,329 | 2,000 1,843 2,000 1,995 1,984 2,000 1,897 1,990 1,997 1,891 |
Сложив числа последнего столбца таблицы 4, найдём сумму 19,597, подставив которую в соотношение
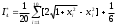
, получим искомую оценку интеграла
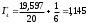 .
.Заметим, что точное значение I=1,147.
§6. Программа вычисления определенного интеграла методом Монте-Карло.
Вычислить определенный интеграл
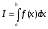 по методу “Монте-Карло” по формуле
по методу “Монте-Карло” по формуле 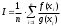 ,
,где n – число испытаний ;g(x) – плотность распределения “вспомогательной” случайной величины X, причем
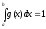 , в программе g(x) = 1/(b-a)
, в программе g(x) = 1/(b-a) Программа написана на языке TURBO PASCAL 7.0
Program pmk;
Uses crt;
Var k,p,s,g,x,Integral : real;
n,i,a,b : integer;
BEGIN
writeln(‘Введите промежуток интегрирования (a;b):’);
readln(a);
readln(b);
writeln(‘Введите количество случайных значений(число испытаний):’);
readln(n);
k:=b-a; {Переменной“k”присвоим значение длины промежутка интегрирования}
writeln(‘k=’,k);
for i:= 1 to n do begin {проведем n испытаний}
g:=random; {g – переменная вещественного типа, случайная величина из промежутка [0;1]}
x:= a + g*(b-a); {По этой формуле получается произвольная величина из [a; b] }
s:=s + (1+x); {s:=s +(x*x)} {Вообще можно подставить любую функцию}
delay(1000); {задержка, чтобы произвольные значения не повторялись}
end; {конец испытаний}
writeln(‘s=’,s); {Сумма функции для n произвольных значений}
Integral:=(1/n)*k*s ;
writeln(‘Интеграл=’,Integral);
readln;
END.
Требуется ввести промежуток интегрирования и количество испытаний, интегрируемая функция уже задана в программе (но ее можно поменять).
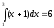 ;
; 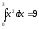 .
. | Функция | k | N=10 | N=100 | N=500 | N=1000 |
| f(x)=1+x | 2 | 5.737 | 5.9702 | 6.02 | 5.99 |
| f(x)=x*x | 3 | 9.6775 | 8.528 | 8.7463 | 8.937 |
§7. Вычисление кратных интегралов методом Монте-Карло.
Пусть функция
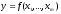
непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл
Геометрически число I представляет собой (m+1)-мерный объём прямого цилиндроида в пространстве
Преобразуем интеграл (1) так, чтобы новая область интегрирования целиком содержалась внутри единичного m-мерного куба. Пусть область S расположена в m-мерном параллелепипеде
Сделаем замену переменных
Тогда, очевидно, m-мерный параллелепипед (2) преобразуется в m-мерный единичный куб
и, следовательно, новая область интегрирования σ, которая находится по обычным правилам, будет целиком расположена внутри этого куба.
Вычисляя якобиан преобразования, будем иметь:
 . Таким образом,
. Таким образом, где
Укажем способ вычисления интеграла (5/) методом случайных испытаний.
Выбираем m равномерно распределённых на отрезке [0, 1] последовательностей случайных чисел:

Точки
1.
2.
(для удобства мы здесь изменяем нумерацию точек).
Заметим, что относительно границы Г области σ следует заранее договориться, причисляются ли граничные точки или часть их к области σ, или не причисляются к ней. В общем случае при гладкой границе Г это не имеет существенного значения; в отдельных случаях нужно решать вопрос с учётом конкретной обстановки.
Взяв достаточно большое число n точек
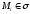 , приближённо можно положить:
, приближённо можно положить: 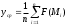 ; отсюда искомый интеграл выражается формулой
; отсюда искомый интеграл выражается формулой 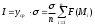 , где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять:
, где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять: 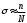 , отсюда
, отсюда 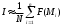 . В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто
. В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто 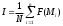 .
.Заключение.
Метод Монте-Карло используется очень часто, порой некритично и неэффективным образом. Он имеет некоторые очевидные преимущества:
а) Он не требует никаких предложений о регулярности, за исключением квадратичной интегрируемости . Это может быть полезным, так как часто очень сложная функция, чьи свойства регулярности трудно установить.
б) Он приводит к выполнимой процедуре даже в многомерном случае, когда численное интегрирование неприменимо, например, при числе измерений, большим 10.
в) Его легко применять при малых ограничениях или без предварительного анализа задачи.
Он обладает, однако, некоторыми недостатками, а именно: