Курсовая работана тему «Операционный метод интегрирования линейных дифференциальных уравнений и линейных систем дифференциальных уравнений.»2023СодержаниеВведение……………………………………………………………………………...3Глава 1. Теоретические аспекты курсовой работы………………………………..5

1. 
   Операционное исчисление. Функции оригинал..…………………………...5
   
2. 
   Преобразование Лапласа. Теоремы преобразования Лапласа……………..6
   
3. 
   Решение линейных систем обыкновенных дифференциальных уравнений…………………………………………………………………….11
   

Глава 2. Эмпирические аспекты курсовой работы……………………………….142.1. Пример №1 решения линейных систем обыкновенных дифференциальных уравнений……………………………………………………142.2. Пример №2 решения линейных систем обыкновенных дифференциальных уравнений……………………………………………………21Заключение………………………………………………………………………….24Список использованных источников……………………………………………...25ВведениеАктуальность исследования заключается в том, что операционное исчисление в настоящее время стало одной из важнейших глав практического математического анализа. Операционный метод непосредственно используется при решении обыкновенных дифференциальных уравнений и систем таких уравнений; его можно использовать и при решении дифференциальных уравнений в частных производных. Операционное исчисление обратило на себя внимание после того, как английский инженер-электрик Хевисайд, используя символическое исчисление, получил ряд важных результатов. Но недоверие к символическому исчислению сохранялось до тех пор, пока Джорджи, Бромвич, Карсон, А. М. Эфрос, А. И. Лурье, В. А. Диткин и другие не установили связи операционного исчисления с интегральными преобразованиями.Идея решения дифференциального уравнения операционным методом состоит в том, что от дифференциального уравнения относительно искомой функции-оригинала f ( t ) переходят к уравнению относительно другой функции F ( p ), называемой изображением f ( t ) . Полученное операционное уравнение обычно уже алгебраическое (значит более простое по сравнению с исходным). Решая его относительно изображения F ( p ) и переходя затем к соответствующему оригиналу, находят искомое решение данного дифференциального уравнения.

---

Все вышеизложенное указывает на актуальность выбранной нами темы – «Операционное исчисление. Преобразование Лапласа. Решение линейных систем обыкновенных дифференциальных уравнений, примеры.» Проблемой нашего исследования является то, что операционное исчисление- одна из важных тем математического анализа, она в трудах ученых не получила должного математического обоснования.Целью нашего исследования является: изучение особенностей операционного метода и преобразований Лапласа при решении линейных систем обыкновенных дифференциальных уравнений.Объект исследования: математический анализ.Предмет исследования: решение линейных систем обыкновенных дифференциальных уравнений использую операционный метод и преобразования Лапласа.В соответствии с целью, объектом и предметом исследования были поставлены следующие задачи:

1. 
   Изучить состояние операционных исчислений.
   
2. 
   Выявить основные преобразования Лапласа.
   
3. 
   Определить теоретические основы операционных исчислений, преобразований Лапласа.
   
4. 
   Привести примеры решений линейных систем обыкновенных дифференциальных уравнений.
   

Глава 1. Теоретическое обоснование курсовой работы

1. 
   Операционные исчисления. Функции оригинал
   

Операционное исчисление- один из наиболее экономичных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами и пользуется большой популярностью у инженеров. Метод был предложен известным американским электротехником и физиком О. Хевисайдом (1892 г.). Он предложил формальные правила обращения с оператором d, dx и некоторыми функциями от этого оператора, используя которые решил ряд важнейших задач электродинамики. Однако операционное исчисление не получило в трудах О. Хевисайда математического обоснования (его математика возникала в физическом контексте, из которого ее нелегко было выделить, многие его результаты оставались недоказанными. Лишь в 20-е годы XX века метод получил обоснование в работах Бромвича и Карсона.Операционный метод решения дифференциальных уравнений можно сравнить с вычислением различных выражений при помощи логарифмов, когда, например, при умножении вычисления ведутся не над самими числами, а над их логарифмами, что приводит к замене умножения более простой операцией – сложением.Так же как и при логарифмировании, при использовании операционного метода нужны:

---

1) таблица оригиналов и соответствующих им изображений;2) знание правил выполнения операций над изображением, соответствующих действиям, производимым над оригиналом.Определение. Функцией- оригиналом - называют функцию f(t) действительного аргумента t, удовлетворяющую условиям:1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е. f(t) 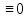при t<02) функция f(t) при t>0 возрастает не быстрее показательнойфункции, т.е. существуют такие постоянные M>0, S ≥0 _, что |f(t)|≤M 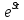при t>03) на любом конечном отрезке положительной полуоси Ot функция f(t)и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода.Простейшей функцией - оригиналом является единичная функция Хевисайда: 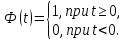(1)Если функция 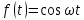 не удовлетворяет условию (1), то произведение  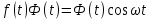уже ему удовлетворяет, т.е. будет оригиналом.

2. 
   Преобразование Лапласа. Теоремы преобразования Лапласа.
   

Преобразование Лапласа — интегральное преобразование, связывающее функцию F(S) комплексного переменного (изображение) с функцией f(x)  действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.Виды преобразований Лапласа:1. Прямое преобразование Лапласа.Преобразованием Лапласа функции действительной переменной f(t), называется функция F(S) комплексной переменной 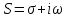 , такая что: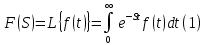Правая часть этого выражения называется интегралом Лапласа. 2. Обратное преобразование Лапласа.Обратным преобразованием Лапласа функции комплексного переменного

---

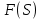
, называется функция 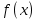 действительного переменного, такая что: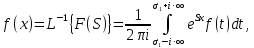



где 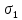 — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.

3. Двустороннее преобразование Лапласа.

Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции 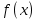 участвуют значения x < 0/

Двустороннее преобразование Лапласа определяется следующим образом:



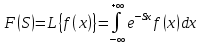
4. Дискретное преобразование Лапласа.

Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают D-преобразование и Z-преобразование.

• 
  D-преобразование
  

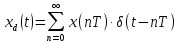
Пусть- решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени 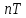 , где n- целое число, а  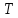- период дискретизации. Тогда применяя преобразование Лапласа получим: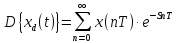

• 
  Z-преобразование
  

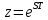
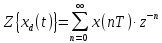
Если применить следующую замену переменных:получим Z-преобразование:Преобразование Лапласа обладает следующими линейными свойствами:

1. 
   Преобразование суммы функций равно сумме преобразований этих функций:
   

2. 
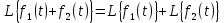
   Постоянный множитель можно выносить за знак преобразования:
   

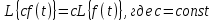
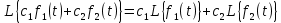
Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований:На конкретном примере рассмотрим преобразование Лапласа.

---

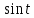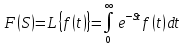
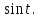
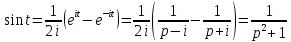
Пример. Найти изображение функции .Решение: Используем формулу:для функции Тогда получим: Перейдем к изучению некоторых основных свойств преобразования Лапласа:

1. 
   Теорема подобия.
   

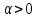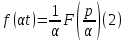
Для любого , Доказательство:Подстановка 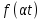в формулу (1) и замена переменного 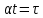приводит к результату (2):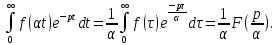

2. 
   Теорема запаздывания.
   

Для любого

3. 
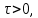
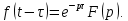
   Теорема смещения.
   

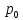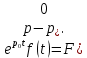
Для любого комплексного числа ,Доказательство свойства (3) элементарно путем подстановки его левой части в интеграл (1).

4. 
   Дифференцирование оригинала.
   

Если функция 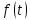непрерывна пр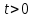и и 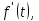или в более общем случае 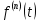являются оригиналами, то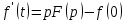 или 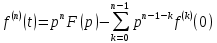,где под 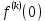понимается предел справа в точке t=0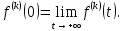

5. 
   Дифференцирование изображения.
   

Дифференцирование изображения сводится к умножению оригинала на (-t), то есть

6. 
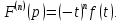
   Интегрирование оригинала.
   

---

Смотрите также файлы

• Анализ внешних и внутренних факторов среды системы менеджмента качества организации.pdf

• Методические указания по выполнению курсовой работы по дисциплине Управление организацией (предприятием).pdf

• Курсовая работа по дисциплине Микроэкономика.docx

• Отчет научноисследовательской работы ( 1 семестр) по направлению подготовки 44. 04. 01 Педагогическое образование.docx

• Жизнь и творчество Николая Гоголя.docx