Ответ:  .  
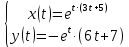Рассмотрим линейное дифференциальное уравнение



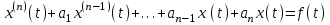
где a_k–действительные числа.

Требуется найти решение данного дифференциального уравнения, удовлетворяющее начальным условиям

x(0)=x₀, x`(0)=x`₀, …, x^(n-1)(0)=x₀^(n-1)

где x₀, x`₀, …, x₀^(n-1) – заданные числа.

Будем предполагать, что искомая функция x(t), все ее производные, а также функция f (t) являются оригиналами.

Пусть 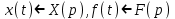. По формулам дифференцирования оригиналов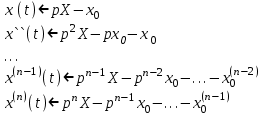



Перейдем от данного дифференциального уравнения к уравнению в изображениях



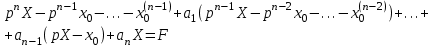
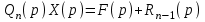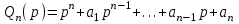Перепишем его так , где , а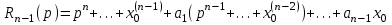

Находим так называемое операторное решение уравнения



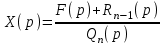
Найдя оригинал x(t) по его изображению X(p) , мы получим тем самым решение задачи Коши для исходного дифференциального уравнения.
Пример 1.

Найти решение дифференциального уравнения x(t)4x(t)5x(t)0,

удовлетворяющее условиям x(0) 0, x(0) 1.

Решение. Запишем уравнение в изображениях









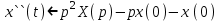
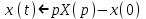
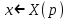
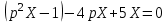
Вынесем Х за скобки





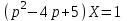
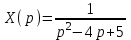
Найдем оригинал используя выведенные ранее значения в таблице приложения:



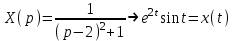
искомое решение -

---

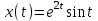
Пример 2.

Решить дифференциальное уравнение y`-2y=0, y(0)=1.

Решение


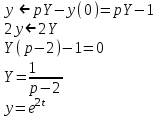
Пример 3.

Решить дифференциальное уравнение y`+y=e^t, y(0)=0.

Решение



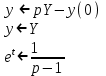
Перейдем к уравнению


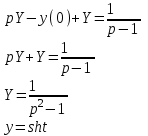
Пример 4.

Найти решение уравнения 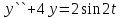при начальных условиях y(0)=-1, y`(0)=0.

Решение

Пусть 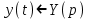, тогда , .

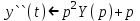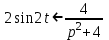Тогда

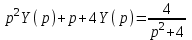
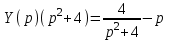- изображающее уравнение. Отсюда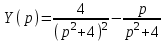



Оригинал для правого слагаемого известен 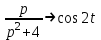, а оригинал для 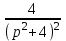удобнее найти по теореме свертывания.

Известно, что 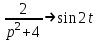, поэтому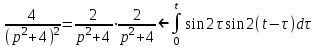



Так как 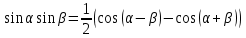, то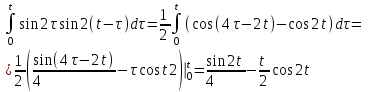



Таким образом,


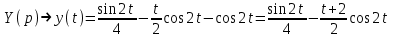
2.2. Пример №2 решения линейных систем обыкновенных дифференциальных уравнений
Методом операционного исчисления найти частное решение системы дифференциальных уравнений 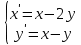  с заданными начальными условиями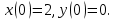  

Решение:  Перейдем от оригиналов к соответствующим изображениям:

---

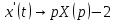
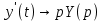
Подставим найденные изображения в исходную систему ДУ:







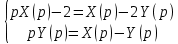
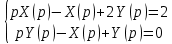
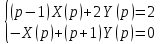
Систему решим по формулам Крамера:

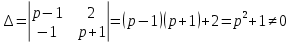, значит, система имеет единственное решение.

Полученный многочлен 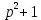  не раскладывается на множители. В этом случае многочлен можно оставить и в таком виде.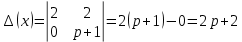









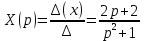
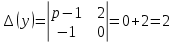
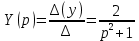
В результате операторное решение системы:



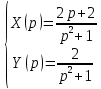
В данном случае метод неопределённых коэффициентов использовать не нужно. В целях применения табличных преобразований перепишем решение в следующем виде:



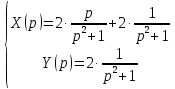
Перейдем от изображений к соответствующим оригиналам:









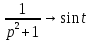
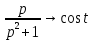
Подставим полученные изображения в операторное решение системы:



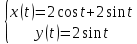
Ответ: частное решение:  . 

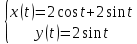Здесь метод операционного исчисления действительно проще, чем «обычный» способ решения.

Заключение
Итак, как мы видим, при решении линейных систем обыкновенных дифференциальных уравнений необходимо от дифференциальных уравнений относительно искомой функции-оригинала 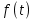  перейти к уравнению относительно другой функции  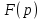, называемой изображением  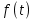. Полученные (операционные) уравнения обычно уже алгебраические (значит более простое по сравнению с исходным). Решая их относительно изображения

---

  и переходя затем к соответствующему оригиналу, находят искомые решения данной системы дифференциальных уравнений.

Можно сделать вывод, что операционный метод решения систем дифференциальных уравнений можно сравнить с вычислением различных выражений при помощи логарифмов, когда, например, при умножении вычисления ведутся не над самими числами, а над их логарифмами, что приводит к замене умножения более простой операцией – сложением.

Так же как и при логарифмировании, при использовании операционного метода нужны:

1) таблица оригиналов и соответствующих им изображений;

2) знание правил выполнения операций над изображением, соответствующих действиям, производимым над оригиналом.

В ходе нашей работы цель, поставленная нами, была достигнута, то есть мы изучили особенности операционного метода и преобразований Лапласа при решении линейных систем обыкновенных дифференциальных уравнений.

Таким образом, задачи были решены, а именно мы:

1. Изучили состояние операционных исчислений.

2. Выявили основные преобразования Лапласа.

3. Определили теоретические основы операционных исчислений, преобразований Лапласа.

4. Привели примеры решений линейных систем обыкновенных дифференциальных уравнений.

Список использованных источников

1. 
   Старков, В.Н. Операционное исчисление и его применения. /В.Н. Старков// Учебн. пособ.; -СПб, 2010.
   
2. 
   Белослюдова, В.В. Специальные разделы математики. Часть 1. Элементы теории функций комплексной переменной. Операционное исчисление: курс лекций для студентов второго курса специальностей 050702, 050716; /В.В. Белослюдова, И.П. Дронсейка// ВКГТУ. – Усть – Каменогорск, 2006.
   
3. 
   Данко, П.Е. Высшая математика в упражнениях и задачах. Часть 2./ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова// Москва, 2005.
   
4. 
   Ершова, В.В. Импульсные функции. Функции комплексной переменной. Операционное исчисление./В.В. Ершова// Под ред. В.И. Азаматовой. Минск, 1976.
   
5. 
   Смышляева, Л.Г. Преобразования Лапласа функций многих переменных. / Л.Г. Смышляева// Изд-во ЛГУ, 1981
   
6. 
   Рудаков, А.В. Операционные системы и среды: Учебник / А.В. Рудаков.// - М.: Инфра-М, 2016. - 480 c.
   
7. 
   Спиридонов, Э.С. Операционные системы / Э.С. Спиридонов, М.С. Клыков, М.Д. Рукин.// - М.: КД Либроком, 2015. - 350 c.
   
8. 
   Батаев, А.В. Операционные системы и среды: Учебник / А.В. Батаев, Н.Ю. Налютин, С.В. Синицын и др.// - М.: Academia, 2018. - 271 c.
   
9. 
   Агафонов, С., А. Обыкновенные дифференциальные уравнения / С. А. Агафонов, Т.В. Муратова. - М.: Academia, 2018.  - 352 c.
   
10. 
     Амелькин, В.В. Дифференциальные уравнения в приложениях / В.В. Амелькин. - М.: КД Либроком, 2012. - 208 c.
    
11. 
    Босс, В. Лекции по математике: Дифференциальные уравнения / В. Босс. - М.: Ленанд, 2019. - 208 c
    
12. 
    Васильева, А.Б. Дифференциальные и интегральные уравнения. Вариационное исчисление в примерах и задачах / А.Б. Васильева и др. - М.: Физматлит, 2005. - 432 c.
    
13. 
    Муратова, Т.В. Дифференциальные уравнения: Учебник и практикум для академического бакалавриата / Т.В. Муратова. - Люберцы: Юрайт, 2016. - 435 c.
    
14. 
    Шалдырван, В.А. Руководство по решению обыкновенных дифференциальных уравнений: Линейные дифференциальные уравнения высших порядков. Граничные задачи для ОДУ. Понятие / В.А. Шалдырван, К.В. Медведев. - М.: КД Либроком, 2012. - 248 c
    
15. 
    Эльсгольц, Л.Э. Дифференциальные уравнения / Л.Э. Эльсгольц. - М.: Издательство ЛКИ, 2019. - 312 c.
    

---

---

Смотрите также файлы

• Анализ внешних и внутренних факторов среды системы менеджмента качества организации.pdf

• Методические указания по выполнению курсовой работы по дисциплине Управление организацией (предприятием).pdf

• Курсовая работа по дисциплине Микроэкономика.docx

• Отчет научноисследовательской работы ( 1 семестр) по направлению подготовки 44. 04. 01 Педагогическое образование.docx

• Жизнь и творчество Николая Гоголя.docx