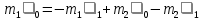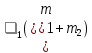V:

Ω = 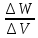= 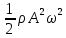, (8.10)

где – плотность среды; A – амплитуда колебаний.

Количество энергии, переносимое волной через единицу площади поверхности S в единицу времени, называется плотностью потока энергии (вектором Умова)

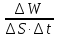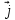j = или = Ω 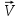, (8.11)

где 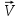– фазовая скорость волны.

j = 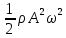V (8.12)

Электромагнитные волны.

Электромагнитная волна представляет собой взаимно перпендикулярные электрические и магнитные поля, меняющиеся по гармоническому закону и

распространяющиеся в направлении перпендикулярном векторам и (рис. 8.2).

– напряженность электрического поля,

– напряженность магнитного поля.

Волновое уравнение электромагнитной волны

Допустим, что волна распространяется вдоль оси Х, электрическое поле направлено вдоль оси Y (E_y ), а магнитное поле направлено вдоль оси Z (H _z ), тогда, используя общий вид волнового уравнения (8.8), можно записать волновое уравнение для E_y в виде:

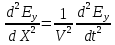(8.13)

и аналогично для H:

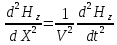(8.14)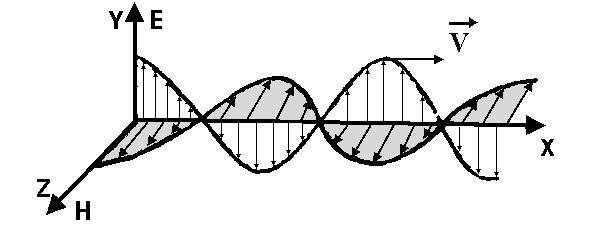



Рис. 8.2 Электромагнитная волна

Уравнение электромагнитной волны

---

Решением волновых уравнений (8.13) и (8.14) являются гармонические функции: 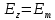cos(ωt-kX+a)

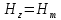cos(ωt-kX+a) (8.15)

где ω - циклическая частота волны, k – волновое число равное 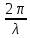или 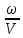, E_m - амплитуда напряженности электрического поля, H_m – амплитуда напряженности магнитного поля. Уравнения (8.15) определяют плоскую электромагнитную волну.

Колебания векторов напряженности электрического и магнитного полей в электромагнитной волне происходят с одинаковыми фазами. На рис.8.2 показана «моментальная фотография» плоской электромагнитной волны. Из рисунка видно, что векторы E и H образуют с направлением волны правовинтовую систему. В определенной точке пространства векторы E и H изменяются со временем по гармоническому закону.

Скорость электромагнитных волн.

Фазовая скорость V в волновом уравнении (8.13) и (8.14) зависит от свойств среды, в которой волны распространяются. Она определяется по формуле:

V = 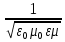= 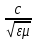, (8.16)

где – диэлектрическая проницаемость среды; 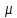– магнитная проницаемость среды; c = 3·10⁸ м/с – скорость света. Из (8.16) следует, что скорость электромагнитной волны в вакууме ( 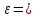1;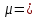 1) равна скорости света с.

Энергия электромагнитной волны.

Электромагнитные волны, как и всякие волны, переносят энергию. Плотность потока энергии 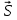(вектор Пойнтинга) можно получить, умножив плотность энергии Ω на скорость электромагнитной волны

---

V. Ω складывается из плотности энергии электрического поля и плотности энергии магнитного поля:

Ω=Ω_E+Ω_H.

Можно показать, что тогда вектор Пойнтинга будет определяться по формуле:

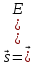] (8.17)

Вектор Пойнтинга всегда направлен в сторону распространения электромагнитной волны и совпадает по направлению с вектором фазовой скорости V (рис.8.2).

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №1

Вариант 8

1. 
   Тонкостенный цилиндр массой 1 кг и радиусом 0,1 м находится на вершине пологой горки высотой 1 м. Цилиндр без начальной скорости скатывается с горки и на горизонтальном участке пути сталкивается с лежащим тонко- стенным цилиндром массой 1,5 кг и радиусом 0,1 м. Удар абсолютно упругий, прямой, центральный. Какой скоростью будет обладать первый цилиндр после удара? Потерями на трение пренебречь.
   

Ответ: ????1 = −0.626 м⁄с

2. 
   От источника с напряжением 10 кВ необходимо подать мощность 500 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от переданной мощности? Рассчитайте длину двухпроводной линия с такими потерями, если в качестве проводника взять алюминий с диаметром поперечного сечения 1 см. Изобразить электрическую схему подключения для данной задачи.
   

Ответ: ???? = 16.53 Ом; ???? = 23 км

3. 
   Колебательный контур состоит из катушки индуктивностью 100 мГн, конденсатора емкостью 5 мкф и сопротивления 10 Ом. Определить, какая часть энергии контура преобразуется в тепло за один период. Через какое время энергия в контуре уменьшится в четыре раза и сколько колебаний произойдет за это время? Изобразить график, затухающих колебания для энергии, соответствующих уравнению ????(????) в пределах двух времён релаксации. Примечание: изобразите на рисунке электрический колебательный контур, в котором возникают свободные затухающие колебания.
   

Ответ: 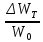= 0.35; ???? = 1.38 · 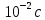; ???? = 3.1

Задача №1

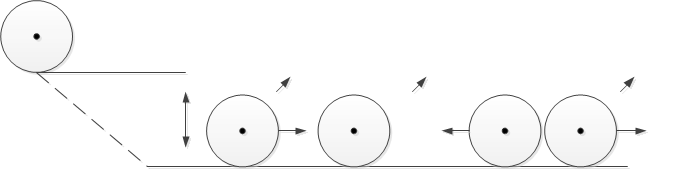
Условие: Тонкостенный цилиндр массой 1 кг и радиусом 0,1 м находится на вершине пологой горки высотой 1 м. Цилиндр без начальной скорости скатывается с горки и на горизонтальном участке пути сталкивается с лежащим тонко- стенным цилиндром массой 1,5 кг и радиусом 0,1 м. Удар абсолютно упругий, прямой, центральный. Какой скоростью будет обладать первый цилиндр после удара? Потерями на трение пренебречь.

---

Дано: Решение:

h = 1м

m1 = 1кг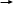

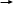
r1 = 0,1м m1 m2 m1 m2

m2 = 1,5 кг R

r2 = 0,1м

= ?

Чтобы найти скорость первого цилиндра, нужно сначала найти скорость налетающего цилиндра. Найдем скорость из закона сохранения энергии.

Покоящийся на вершине горки первый цилиндр имеет потенциальную энергию 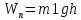. Когда цилиндр скатится с горки, его потенциальная энергия полностью превратится в кинетическую энергию, так как система замкнута и потерями на трение пренебрегаем по условию задачи.

Кинетическая энергия первого цилиндра складывается из кинетической энергии поступательного движения первого цилиндра с горки и вращательного движения толстостенного цилиндра вокруг центра масс. Используем теорему Кенига:

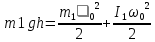(1)

Момент инерции толстостенного цилиндра относительно оси, проходящей через центр масс, 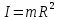, а угловая скорость связана с линейной скоростью соотношением: U=R .

Подставляем все законы сохранения энергии (1):

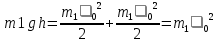(2)



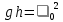
Скорость налетающего цилиндра:



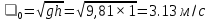
Для нахождения скорости первого цилиндра после удара воспользуемся законами сохранения энергии и импульса для абсолютно упругого удара.

Поскольку масса налетающего цилиндра меньше массы покоящегося цилиндра, то после удара первый цилиндр будет двигаться в обратном направлении.

---

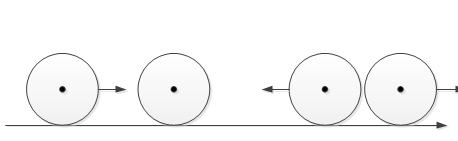
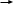
m1 m2 m1 m2
Закон сохранения импульса в проекции на горизонтальную ось ОХ`:

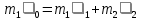
Закон сохранения энергии учитывает, что при абсолютно упругом ударе сохраняется кинетическая энергия, причем движутся одинаковые по размеру цилиндры (удар прямой, центральный). Кинетическая энергия цилиндра складывается из кинетической энергии поступательного движения цилиндра вдоль оси ОХ и вращательного движения цилиндра вокруг центра масс.

Используя теорему Кенига, запишем:

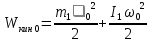- кинетическая энергия первого цилиндра до соударения.
Используя рассуждения, аналогичные (2), получим:

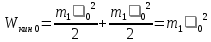
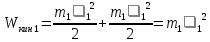- кинетическая энергия первого цилиндра после соударения.

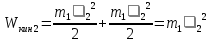- кинематическая энергия второго цилиндра после соударения

Запишем закон сохранения энергии при абсолютно упругом соударении двух цилиндров:



= +

- =
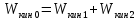
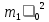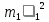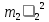
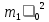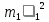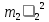
Во втором уравнении распишем разность квадратов и воспользуемся равенством из первого уравнения:

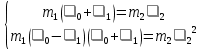
Получим:

=

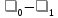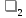
Подставим значения в закон сохранения импульса:

---

Смотрите также файлы

• Задание 1 Определять сущность экономической безопасности как научной категории.docx

• Список педагогов мбоу сош 2 с. Самашки, прошедших кпк в 20202022 уч гг.docx

• Определите преимущества и недостатки использования стратегической ориентации на проектную форму организации и оплаты труда производственного персонала, заполнив для этого соответствующие графы таблицы.docx

• Халмуратов Азизбек Халмуратович москва 2023 Практическое занятие.docx

• Отчёт по статьям Статья 2.pdf