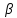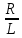2 = и =

После введения обозначений дифференциальное уравнение затухающих колебаний в контуре принимает вид:

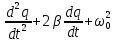= (7.32)

Уравнение колебания заряда

Заряд на пластинах конденсатора меняется по закону

q = 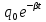cos (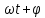 ) (7.33)

Это уравнение является решением дифференциального уравнения (7.32), где:

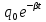= - амплитудное значение заряда,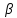

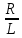= - коэффициент затухания

R - омическое сопротивление

???? - индуктивность катушки

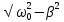= - циклическая частота затухающих колебаний

= - циклическая частота собственных колебаний, зависящая от параметров контура L, C

Подставив значения и 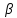в формулу частоты колебаний, получим:

=

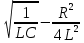
(7.34)

---

Логарифмический декремент затухания

Для характеристики затухания вводится физическая величина – логарифмический декремент затухания δ, равный натуральному логарифму отношения двух амплитуд, следующих друг за другом через период:

00 = ln (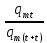 ) (7.35)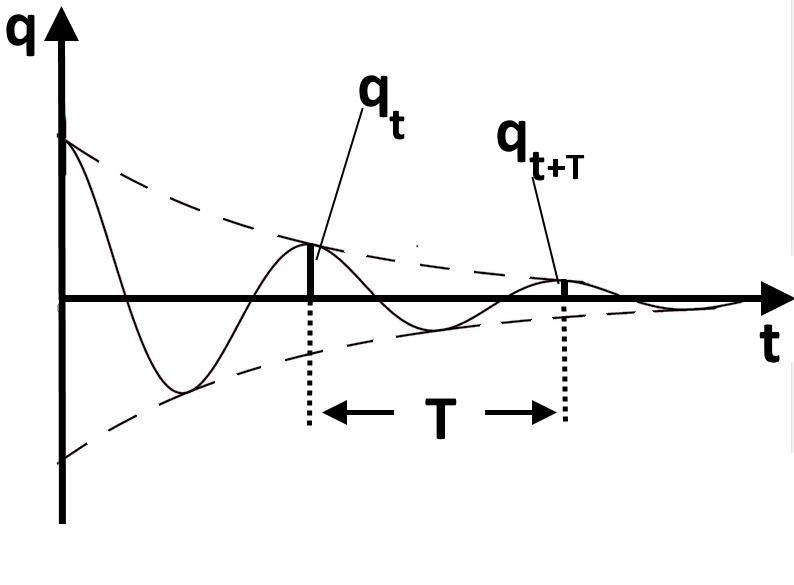



Рис.7.17 График затухающих колебаний заряда (начальная фаза колебаний φ = 0).

Время релаксации - это время, в течении которого амплитудное значение уменьшается в е раз ( e ≈ 2.72 , основание натурального логарифма). Связь времени релаксации и коэффициента затухания выражается формулой: 1

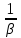???? = (7.36)

Добротность контура

Добротность контура ???? показывает, как быстро убывает энергия в контуре за один период колебаний. Добротность контура ???? определяется как отношение начальной энергии ????₀ к потерям энергии за один период колебаний умноженное на 2????:

???? = = = =

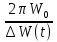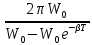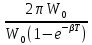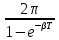
В случае слабого затухания ( << ₀, обычно как минимум в 100 раз), экспоненту можно разложить в ряд Тейлора и оставить первые два члена ряда.

1-e^-2βT 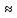1-(1-2βT) = 2βT (7.37а)

Тогда, подставив выражение (7.37a) в формулу добротности, получим

2???? 2???? ???? ????

???? = 1−????−2???????? ≈ 2???????? = ???????? = ????

Таким образом, при слабом затухании добротность определяется по формуле:

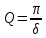(7.37)

где δ - логарифмический декремент затухания.

Напряжение при затухающих колебаниях

Изменение со временем разности потенциалов на пластинах конденсатора можно записать, если учесть, что

---

q =CU, тогда

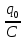
U = 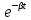cos ( )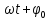

Обозначив 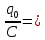U₀ - максимальное напряжение в контуре, значение разности потенциалов запишется в виде:

U =U₀ 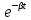cos ( ), (7.38)

где U₀ 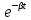⁼U _m - амплитуда напряжения.

Сила тока в катушке определяется по формуле

I =I₀ 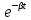sin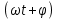 (7.39)

где 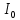= 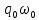максимальное значение тока в контуре; I₀ 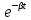- амплитудное значение тока

Энергия при затухающих колебаниях

Полная энергия контура будет складываться из энергии магнитного поля

(МП) и энергии электрического поля (ЭП)

W =W_B+W_E ,

где W _{B =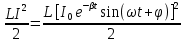} – энергия МП;

W E= 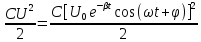- энергия ЭП

Полную энергию в любой момент времени можно определить через максимальную энергию электрического поля в контуре в данный момент времени:

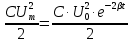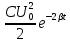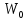
W полн = = = 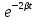, (7.40)

где W₀ – полная энергия контура в момент времени t=0.
8. ВОЛНЫ
Волной называют процесс распространения колебаний. В упругих средах могут распространяться механические колебания, электромагнитные колебания могут распространяться как непроводящих средах, так и в вакууме.

Волны в упругих средах Уравнение волны

---

Будем рассматривать волну, распространяющуюся только в одном направлении (одномерный случай). Выберем в упругой среде направление «Х», вдоль которого распространяется колебательный процесс со скоростью υ и с циклической частотой ????. В точке «О» расположен источник колебания, рис.8.1, который заставляет точку «О» совершаться гармонические колебания по закону: ????(????) = ????cos(????????+????), где ????(????) – смещение точки «О» вдоль оси Y от положения равновесия.



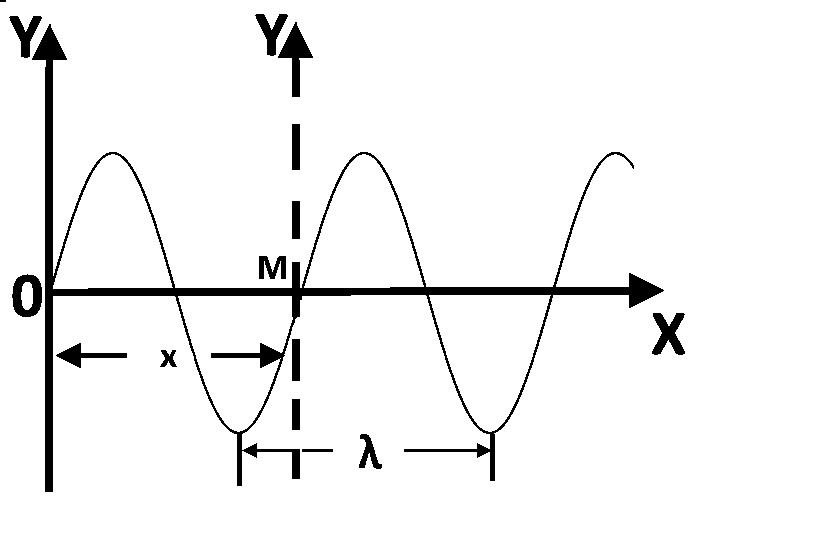
Рис.8.1 Волновое движение

Через время ???? = 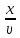колебательный процесс дойдет до точки М, она начнет совершать колебания около положения равновесия по закону

????(????) = ????cos(????(????−????) +????) (8.1)

Смещение точки М запишется тогда в виде:

???? (????, ????) = ????cos (????????− 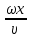+????) (8.2)
Характеристики волнового процесса. υ – скорость распространения колебательного процесса (или скорость распространения данной фазы колебаний) называется скоростью волны (фазовая скорость).

???? – длина волны – это расстояние, проходимое волной за время одного периода колебаний

???? = ????∙????

Или по-другому, это – кратчайшее расстояние между точками, разность фаз колебаний которых составляет 2π (рис.8.1).

Т – период – это время одного колебания, за период колебательный процесс распространяется на расстояние, равное длине волны,

ωt - 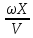+ a – фаза колебания данной точки среды, V

_a – начальная фаза колебаний,

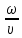???? = – волновое число.

ω - циклическая частота, её связь с периодом колебаний T: ω = .

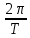Используя данные характеристики, уравнение (8.2) можно записать так: ???? (????, ????) = ????cos ( )

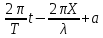или

???? (????, ????) = ????cos(????????−????????+????) (8.3)

Это уравнение плоской бегущей волны, где ???? (????, ????) – смещение точки, находящейся на расстоянии Х от источника колебаний, в любой момент времени (см. рис. 8.1).

---

Скорость и ускорение колеблющихся точек. Скорость колеблющейся точки можно определить так, ???? = 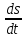т.е.

υ=-Aωsin (ωt -kX +a), (8.4)

-Aω = υ_m– амплитудное значение скорости. В любой момент времени скорость определяется по формуле:

υ=υ_msin(ωt -kX +a) (8.5)

Ускорение колеблющейся точки равно a = 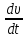, т.е.

a = - υ_mωcos (ωt -kX +a), (8.6)

где υ_mω = a_m – амплитудное (максимальное) значение ускорения. Зависимость ускорения от времени запишется в виде:

a =a_mcos(ωt -kX +a) (8.7)

Волновое уравнение

Волновым уравнением называется дифференциальное уравнение, решением которого описываются всевозможные типы волн, существующих в природе. Оно записывается в виде

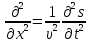(8.8)

где ???? (????, ????) – решение волнового уравнения; 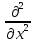– вторая производная по координате x от ????(????,????); 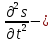вторая производная по времени t от ????(????,????); ???? – фазовая скорость волны.

Уравнение плоской бегущей волны (8.4), которое мы получили выше, также является решением этого уравнения. Это проверяется непосредственной подстановкой (8.4) в (8.8). Общий вид решения уравнения (8.8) записывается в виде

???? (????, ????) = ???? (ωt -kX)(8.9)

где ???? (ωt - kX) – произвольная гладкая дифференцируемая функция, имеющая вторые производные по координате x и по времени t.

Энергия упругой волны

Среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной, следовательно, волна переносит с собой энергию.

Введём понятие плотности энергии волны Ω. Это волновая энергия W, заключенная в единице объема

---

Смотрите также файлы

• Задание 1 Определять сущность экономической безопасности как научной категории.docx

• Список педагогов мбоу сош 2 с. Самашки, прошедших кпк в 20202022 уч гг.docx

• Определите преимущества и недостатки использования стратегической ориентации на проектную форму организации и оплаты труда производственного персонала, заполнив для этого соответствующие графы таблицы.docx

• Халмуратов Азизбек Халмуратович москва 2023 Практическое занятие.docx

• Отчёт по статьям Статья 2.pdf