Файл: Кафедра физики расчётнографическая работа 1 Вариант 8 Мальцева Ю. Е. Группа зи221 Номер студенческого билета.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 142
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 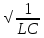 - собственная частота колебаний, зависящая от параметров контура; L – индуктивность катушки, C – емкость конденсатора.
- собственная частота колебаний, зависящая от параметров контура; L – индуктивность катушки, C – емкость конденсатора.
Уравнение колебаний заряда q, напряжения U, силы тока I
Решением дифференциального уравнения (7.12) является уравнение вида:
q =qmcos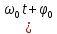 ) (7.14)
) (7.14)
Это уравнение называется уравнением колебания заряда, где qm – амплитудное значение заряда.
Напряжение U на обкладках конденсатора связана с зарядом q и с емкостью конденсатора с соотношением U = , поэтому уравнение колебания напряженияимеет вид:
, поэтому уравнение колебания напряженияимеет вид:
U =Umcos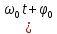 ) (7.15)
) (7.15)
где Um =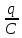 – амплитудное значение разности потенциалов.
– амплитудное значение разности потенциалов.
Сила тока в контуре тоже будет меняться по гармоническому закону, т.к.
I = , то I = -
, то I = -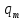
 sin
sin 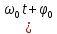 )
)
где
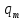
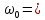 Im– амплитудное значение силы тока.
Im– амплитудное значение силы тока.
Следовательно, зависимость силы тока в катушке индуктивности запишется уравнением:
I = -Imsin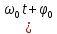 ) (7.16)
) (7.16)
Проведем аналогию зависимостей физических величин, характеризующих механические и электромагнитные колебания.
Таблица 7.1. Электромеханические аналогии
Энергия контура
Полная энергия колебаний в контуре складывается из энергии электрического поля конденсатора q2
W эл =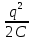 (7.17)
(7.17)
и магнитного поля соленоида
W маг = (7.18)
(7.18)
Так как заряд и ток в контуре меняются по гармоническому закону, то энергия электрического поля и энергия магнитного поля также будет меняться по гармоническому закону со временем. В какие-то моменты времени полная энергия будет равна максимальной энергией электрического поля W эл(m) =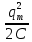 , а в какие-то моменты полная энергия будет равна максимальной энергии магнитного поля Wмаг(m) =
, а в какие-то моменты полная энергия будет равна максимальной энергии магнитного поля Wмаг(m) = 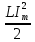
СЛОЖЕНИЕ КОЛЕБАНИЙ
Возможны случаи: 1) когда тело участвует одновременно в нескольких колебаниях, происходящих вдоль одного и того же направления; 2) взаимно перпендикулярные колебания (или вдоль различных направлений). Сложение колебаний одного направления.
Сложение колебаний с одинаковыми частотами.
Допустим, что тело участвует в двух гармонических колебаниях:
X 1 смещение в первом из колебаний при отсутствии второго;
X 2 смещение при втором колебании в отсутствии первого.
Тогда при одновременно происходящих колебательных процессах в каждое мгновение результирующее смещение X будет равно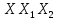 . Результирующее колебание будет тоже гармоническим, а значит, можем для него записать:
. Результирующее колебание будет тоже гармоническим, а значит, можем для него записать:
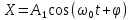 (7.19)
(7.19)
где A амплитуда результирующего колебания, циклическая частота результирующего колебания,
циклическая частота результирующего колебания,  - начальная фаза результирующего колебания.
- начальная фаза результирующего колебания.
Задача нахождения результирующего колебания сводится к определению величин A, ,
, .
.
Пусть заданы уравнения колебаний:
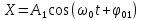
(7.20)
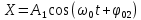 (7.20)
(7.20)
Сложение колебаний одного направления и одинаковых частот производят по методу векторных диаграмм. Каждое колебание изображается в виде вектора, имеющего длину, равную амплитуде колебания, вращающегося вокруг начала координат с угловой скоростью, равной круговой частоте колебаний, а начальное положение вектора определяется его начальной фазой колебаний. При сложении двух колебаний с одинаковыми частотами получим результирующее колебание, которое будет являться диагональю параллелограмма. Векторы вращаются с одной и той же угловой скоростью, поэтому и результирующий вектор будет вращаться с той же угловой скоростью. Следовательно, результирующее колебание будет тоже гармоническим, смещение меняется по закону
X = Acos(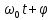 ) . (7.21)
) . (7.21)
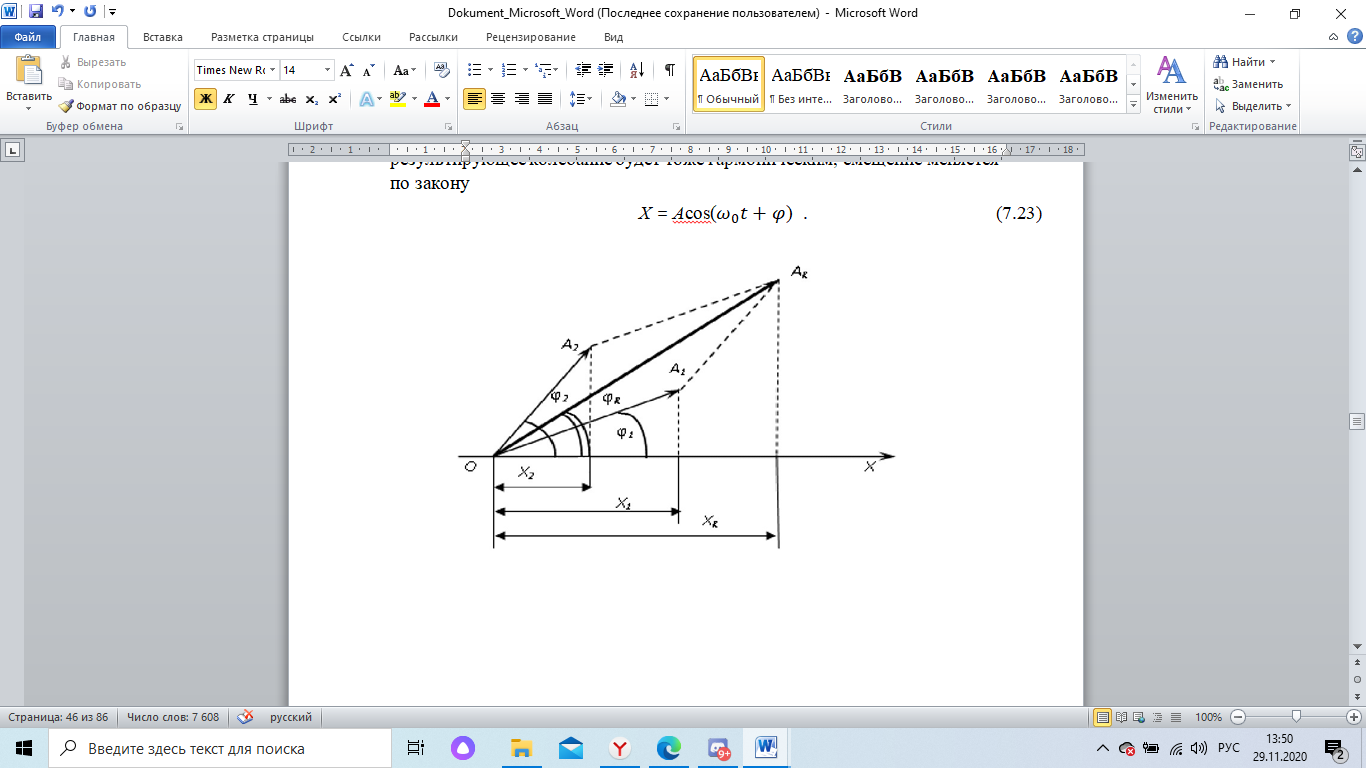
Рис.7.4 Векторная диаграмма сложения колебаний одного направления с одинаковыми частотами ( на рис.7.6 использованы обозначения начальных фаз φ1 и φ2 вместо φ01и φ02).
Амплитуду и фазу результирующего колебания при сложении колебаний одного направления с одинаковыми частотами находят по формулам:
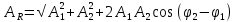
tg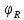 =
= 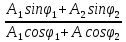 (7.22)
(7.22)
Частота результирующего колебания ω = ω0.
Биения
В случае, когда складываемые колебания происходят по законам
X1 = Acos( 1t) и X 2=Acos (
1t) и X 2=Acos ( 2t) с небольшой разностью частот
2t) с небольшой разностью частот 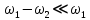 ,
, 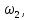 возникают биения. Результирующее колебание описывается уравнением
возникают биения. Результирующее колебание описывается уравнением
X=2Acos (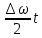 ) cos (
) cos (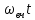 ), (7.23)
), (7.23)
где 2Acos (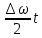
) =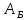 - амплитуда биения,
- амплитуда биения,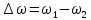 - разность частот складываемых колебаний; ????вч =
- разность частот складываемых колебаний; ????вч =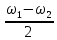 – частота высокочастотных колебаний.
– частота высокочастотных колебаний.
Следовательно, при биениях амплитуда меняется по гармоническому закону с частотой биений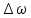 =
= 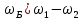
Период биений равен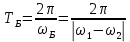
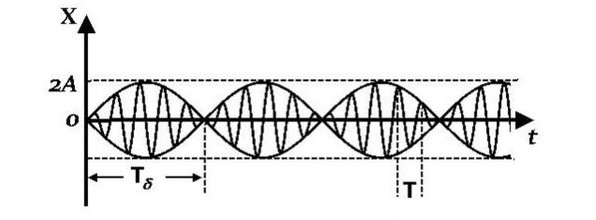
Рис.7.5 График результирующего колебания при сложении колебаний одинакового направления с близкими частотами.
На рис.7.5 показан период биения Т Б - время, за которое происходит одно полное изменение амплитуды результирующего колебания, время Т - это время одного колебания. В рассмотренном примере за период биения происходит пять колебаний.
Сложение взаимно перпендикулярных колебаний с одинаковыми частотами.
Тело участвует одновременно в колебаниях вдоль оси X, которые происходят по закону:
Х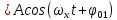 (7.24)
(7.24)
и вдоль оси Y, по закону
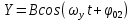 , (7.26)
, (7.26)
частота колебаний вдоль осей X и Y одинаковая (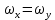 ), амплитуды соответственно равные A и B, разность начальных фаз
), амплитуды соответственно равные A и B, разность начальных фаз
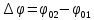
Если сложить (7.23) и (7.24), то можно получить уравнение при взаимно перпендикулярных колебаниях с одинаковыми частотами Доказано, что в этом случае тело будет двигаться по траектории, уравнение которой имеет вид:
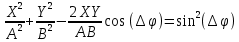 (7.27)
(7.27)
Уравнение (7.26) представляет собой траекторию эллипса, не приведённого к главным осям. Исследуя формулу траектории, можно доказать, что при разности фаз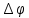 = 0 колеблющаяся точка перемещается по прямой:
= 0 колеблющаяся точка перемещается по прямой:
Y =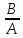 X; (7.28)
X; (7.28)
При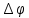
=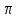 уравнение траектории будет иметь вид
уравнение траектории будет иметь вид
Y =- X; (7.29)
X; (7.29)
при =
= 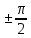 траектория представляет собой эллипс, приведённый к главным осям, уравнение которого имеет вид:
траектория представляет собой эллипс, приведённый к главным осям, уравнение которого имеет вид:
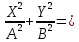 1 (7.30)
1 (7.30)
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ
В любой реальной системе всегда имеются силы сопротивления, энергия системы уменьшается, т.к. частично расходуется на работу против сил трения, амплитуда колебаний со временем убывает.
Любой реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постоянно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания в контуре затухают.
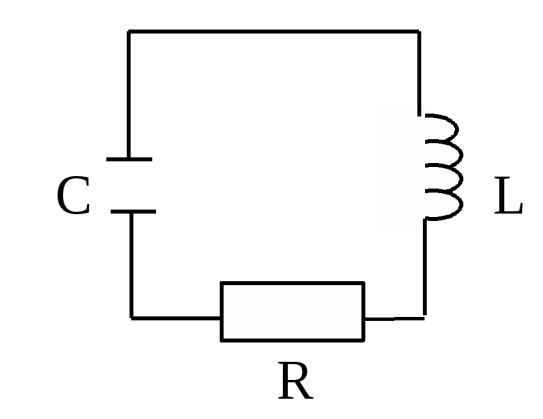
Рис.7.6 Схема реального контура, обладающего активным сопротивлением R.
Дифференциальное уравнение колебания заряда
Для математического описания электрических процессов в контуре применим 2 правило Кирхгофа: «Сумма падений напряжения в контуре равна сумме действующих в нем ЭДС». В колебательном контуре имеются два падения q
напряжения: на конденсаторе UC = , и на сопротивлении, равное UC = IR.
, и на сопротивлении, равное UC = IR.
При изменении силы тока в контуре в катушке индуктивности возникает ЭДС самоиндукции.
IR+UC = -L (7.31)
(7.31)
Сила тока по определению является производной от заряда по времени: I =
Подставив выражения для тока I и напряжения UC в формулу (1), получим дифференциальное уравнение в виде:
L +
+ 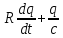 = 0
= 0
Разделим уравнение на коэффициент при старшей производной (индуктивность катушки) и введем обозначения:
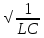 - собственная частота колебаний, зависящая от параметров контура; L – индуктивность катушки, C – емкость конденсатора.
- собственная частота колебаний, зависящая от параметров контура; L – индуктивность катушки, C – емкость конденсатора. Уравнение колебаний заряда q, напряжения U, силы тока I
Решением дифференциального уравнения (7.12) является уравнение вида:
q =qmcos
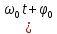 ) (7.14)
) (7.14) Это уравнение называется уравнением колебания заряда, где qm – амплитудное значение заряда.
Напряжение U на обкладках конденсатора связана с зарядом q и с емкостью конденсатора с соотношением U =
 , поэтому уравнение колебания напряженияимеет вид:
, поэтому уравнение колебания напряженияимеет вид: U =Umcos
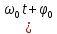 ) (7.15)
) (7.15) где Um =
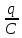 – амплитудное значение разности потенциалов.
– амплитудное значение разности потенциалов. Сила тока в контуре тоже будет меняться по гармоническому закону, т.к.
I =
 , то I = -
, то I = -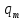
 sin
sin 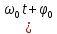 )
)где

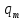
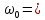 Im– амплитудное значение силы тока.
Im– амплитудное значение силы тока. Следовательно, зависимость силы тока в катушке индуктивности запишется уравнением:
I = -Imsin
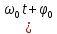 ) (7.16)
) (7.16) Проведем аналогию зависимостей физических величин, характеризующих механические и электромагнитные колебания.
Таблица 7.1. Электромеханические аналогии
| Электрические колебания | Механические колебания |
| q | x |
| R | r |
| L | m |
| 1  C | k |
| I | Υ |
| ????эл | W п |
| ????маг | W кин |
Энергия контура
Полная энергия колебаний в контуре складывается из энергии электрического поля конденсатора q2
W эл =
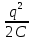 (7.17)
(7.17) и магнитного поля соленоида
W маг =
 (7.18)
(7.18) Так как заряд и ток в контуре меняются по гармоническому закону, то энергия электрического поля и энергия магнитного поля также будет меняться по гармоническому закону со временем. В какие-то моменты времени полная энергия будет равна максимальной энергией электрического поля W эл(m) =
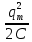 , а в какие-то моменты полная энергия будет равна максимальной энергии магнитного поля Wмаг(m) =
, а в какие-то моменты полная энергия будет равна максимальной энергии магнитного поля Wмаг(m) = 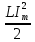
СЛОЖЕНИЕ КОЛЕБАНИЙ
Возможны случаи: 1) когда тело участвует одновременно в нескольких колебаниях, происходящих вдоль одного и того же направления; 2) взаимно перпендикулярные колебания (или вдоль различных направлений). Сложение колебаний одного направления.
Сложение колебаний с одинаковыми частотами.
Допустим, что тело участвует в двух гармонических колебаниях:
X 1 смещение в первом из колебаний при отсутствии второго;
X 2 смещение при втором колебании в отсутствии первого.
Тогда при одновременно происходящих колебательных процессах в каждое мгновение результирующее смещение X будет равно
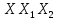 . Результирующее колебание будет тоже гармоническим, а значит, можем для него записать:
. Результирующее колебание будет тоже гармоническим, а значит, можем для него записать: 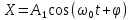 (7.19)
(7.19)где A амплитуда результирующего колебания,
 циклическая частота результирующего колебания,
циклическая частота результирующего колебания,  - начальная фаза результирующего колебания.
- начальная фаза результирующего колебания. Задача нахождения результирующего колебания сводится к определению величин A,
 ,
, .
. Пусть заданы уравнения колебаний:
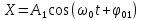
(7.20)
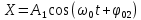 (7.20)
(7.20) Сложение колебаний одного направления и одинаковых частот производят по методу векторных диаграмм. Каждое колебание изображается в виде вектора, имеющего длину, равную амплитуде колебания, вращающегося вокруг начала координат с угловой скоростью, равной круговой частоте колебаний, а начальное положение вектора определяется его начальной фазой колебаний. При сложении двух колебаний с одинаковыми частотами получим результирующее колебание, которое будет являться диагональю параллелограмма. Векторы вращаются с одной и той же угловой скоростью, поэтому и результирующий вектор будет вращаться с той же угловой скоростью. Следовательно, результирующее колебание будет тоже гармоническим, смещение меняется по закону
X = Acos(
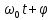 ) . (7.21)
) . (7.21)
Рис.7.4 Векторная диаграмма сложения колебаний одного направления с одинаковыми частотами ( на рис.7.6 использованы обозначения начальных фаз φ1 и φ2 вместо φ01и φ02).
Амплитуду и фазу результирующего колебания при сложении колебаний одного направления с одинаковыми частотами находят по формулам:
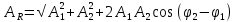
tg
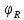 =
= 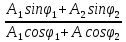 (7.22)
(7.22) Частота результирующего колебания ω = ω0.
Биения
В случае, когда складываемые колебания происходят по законам
X1 = Acos(
 1t) и X 2=Acos (
1t) и X 2=Acos ( 2t) с небольшой разностью частот
2t) с небольшой разностью частот 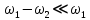 ,
, 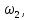 возникают биения. Результирующее колебание описывается уравнением
возникают биения. Результирующее колебание описывается уравнением X=2Acos (
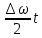 ) cos (
) cos (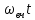 ), (7.23)
), (7.23) где 2Acos (
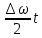
) =
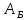 - амплитуда биения,
- амплитуда биения,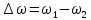 - разность частот складываемых колебаний; ????вч =
- разность частот складываемых колебаний; ????вч =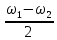 – частота высокочастотных колебаний.
– частота высокочастотных колебаний. Следовательно, при биениях амплитуда меняется по гармоническому закону с частотой биений
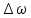 =
= 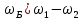
Период биений равен
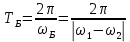

Рис.7.5 График результирующего колебания при сложении колебаний одинакового направления с близкими частотами.
На рис.7.5 показан период биения Т Б - время, за которое происходит одно полное изменение амплитуды результирующего колебания, время Т - это время одного колебания. В рассмотренном примере за период биения происходит пять колебаний.
Сложение взаимно перпендикулярных колебаний с одинаковыми частотами.
Тело участвует одновременно в колебаниях вдоль оси X, которые происходят по закону:
Х
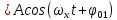 (7.24)
(7.24) и вдоль оси Y, по закону
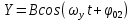 , (7.26)
, (7.26) частота колебаний вдоль осей X и Y одинаковая (
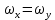 ), амплитуды соответственно равные A и B, разность начальных фаз
), амплитуды соответственно равные A и B, разность начальных фаз 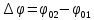
Если сложить (7.23) и (7.24), то можно получить уравнение при взаимно перпендикулярных колебаниях с одинаковыми частотами Доказано, что в этом случае тело будет двигаться по траектории, уравнение которой имеет вид:
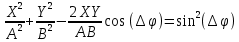 (7.27)
(7.27) Уравнение (7.26) представляет собой траекторию эллипса, не приведённого к главным осям. Исследуя формулу траектории, можно доказать, что при разности фаз
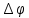 = 0 колеблющаяся точка перемещается по прямой:
= 0 колеблющаяся точка перемещается по прямой: Y =
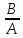 X; (7.28)
X; (7.28) При
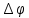
=
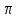 уравнение траектории будет иметь вид
уравнение траектории будет иметь вид Y =-
 X; (7.29)
X; (7.29) при
 =
= 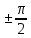 траектория представляет собой эллипс, приведённый к главным осям, уравнение которого имеет вид:
траектория представляет собой эллипс, приведённый к главным осям, уравнение которого имеет вид: 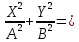 1 (7.30)
1 (7.30)ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ
В любой реальной системе всегда имеются силы сопротивления, энергия системы уменьшается, т.к. частично расходуется на работу против сил трения, амплитуда колебаний со временем убывает.
Любой реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постоянно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания в контуре затухают.

Рис.7.6 Схема реального контура, обладающего активным сопротивлением R.
Дифференциальное уравнение колебания заряда
Для математического описания электрических процессов в контуре применим 2 правило Кирхгофа: «Сумма падений напряжения в контуре равна сумме действующих в нем ЭДС». В колебательном контуре имеются два падения q
напряжения: на конденсаторе UC =
 , и на сопротивлении, равное UC = IR.
, и на сопротивлении, равное UC = IR. При изменении силы тока в контуре в катушке индуктивности возникает ЭДС самоиндукции.
IR+UC = -L
 (7.31)
(7.31) Сила тока по определению является производной от заряда по времени: I =

Подставив выражения для тока I и напряжения UC в формулу (1), получим дифференциальное уравнение в виде:
L
 +
+ 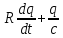 = 0
= 0Разделим уравнение на коэффициент при старшей производной (индуктивность катушки) и введем обозначения: