ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
по лабораторной работе №7
по дисциплине «Теоретические основы электротехники»
Тема: Исследование резонансных явлений в простых
электрических цепях
| Студент гр. 1406 | | Егоров И. А. |
| Преподаватель | | Соседов Н.А. |
Санкт-Петербург
2023
Цель работы: исследование резонанса и АЧХ последовательного колебательного контура.
Резонанс – это состояние RLC-цепи в установившемся синусоидальном режиме, при котором напряжение и ток на входе цепи совпадают по фазе.
Схема исследуемой цепи изображена:
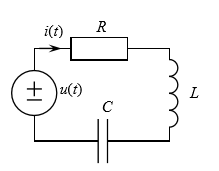
Резонанс в цепи – резонансом напряжений, а цепь – последовательный контур. При резонансе вещественными становятся комплексное сопротивление последовательной цепи:
Отсюда резонансная частота цепи:
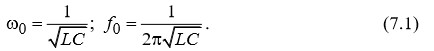
При резонансе модуль проводимости цепи на становится максимальным:
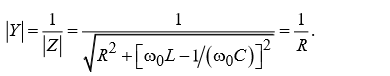
из этого следует, что при ω=ω0максимальным будет ток:
Напряжения на емкости и индуктивности в цепи при резонансе компенсируют друг друга и могут быть во много раз больше напряжения источника. Добротность Q последовательного контура - отношение действующего значения напряжения любого из реактивных элементов к напряжению источника при ω=ω0 :
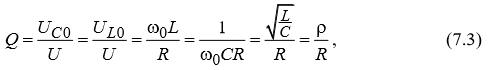
где ρ- характеристическое сопротивление контура.
Если в режиме резонанса измерены напряжения на входе U и на конденсаторе Uco , ток Io, резонансная частота f0, то из приведенных соотношений можно определить все параметры последовательного контура: сопротивление R , добротность Q и характеристическое сопротивление ρ, а емкость и индуктивность:
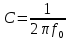 ,
, 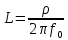
При отклонении частоты от резонансной реактивное сопротивление последовательного контура и реактивная проводимость параллельного не равны нулю, поэтому ток первого и напряжение второго уменьшаются.
АЧХ (резонансная кривая) последовательного контура есть зависимость модуля проводимости от частоты:
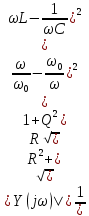
«Острота» резонансной кривой определяет частотную избирательность цепи. По АЧХ можно определить добротность контура. Она равна отношению
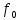 к полосе пропускания
к полосе пропускания 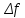 , измеренной по уровню 0,707 от максимума АЧХ:
, измеренной по уровню 0,707 от максимума АЧХ: 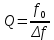
П
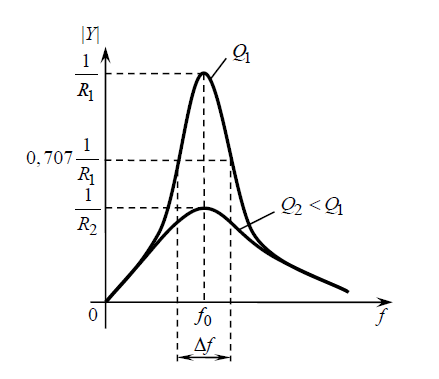 римерный вид АЧХ, построенных по выражению при различных значениях R, представлен
римерный вид АЧХ, построенных по выражению при различных значениях R, представленОбработка результатов
-
Исследование резонанса напряжений и АЧХ контура с малыми потерями
| при резонансе таб. №1 | |||
| U, В | 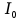 , мA , мA | 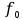 , Гц , Гц | 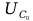 |
| 2 | 10,6 | 3636 | 36,3 |
Расчётные формулы.
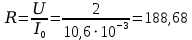
Ом
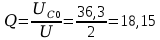 ;
;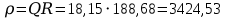 Ом
Ом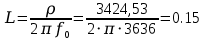 Гн
Гн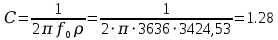 мкФ
мкФ| R, Ом | Q | C, мкФ | L, Гн | 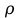 , Ом , Ом |
| 188,68 | 18,15 | 1,28 | 0,15 | 3424,53 |
Амплитудно-частотная характеристика (резонансная кривая) последовательного контура есть зависимость модуля проводимости от частоты:
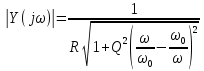 ;
;| Измеренные | Вычисл. | ||
| U, В | 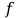 , Гц , Гц | 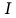 , мА , мА | Y(jw), мСм |
| 2 | 1818 | 0,38 | 0,000194543 |
| 2 | 1980 | 0,45 | 0,000225843 |
| 2 | 2440 | 0,71 | 0,0003557 |
| 2 | 3030 | 1,6 | 0,000787552 |
| 2 | 3333 | 2,9 | 0,001597908 |
| 2 | 3508 | 9,16 | 0,003229591 |
| 2 | 3636 | 10,6 | 0,0053 |
| 2 | 3800 | 6,36 | 0,002806518 |
| 2 | 4000 | 3,8 | 0,001468177 |
| 2 | 4404 | 1,48 | 0,000749661 |
| 2 | 5000 | 1 | 0,000449057 |
| 2 | 5970 | 0,57 | 0,000282317 |
| 2 | 7272 | 0,39 | 0,000194543 |
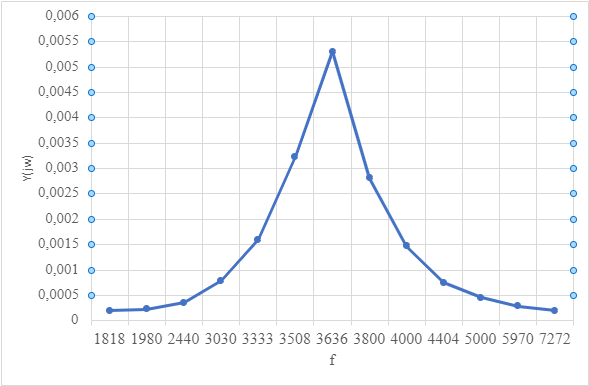
Рисунок 1 – АЧХ контура с малыми потерями.
-
Исследование резонанса напряжений и АЧХ контура с большими потерями.
| при резонансе таб №2 | |||
| U, В |  , мА , мА | 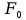 , Гц , Гц |  , В , В |
| 2 | 3,09 | 3636 | 9,87 |
Расчётные формулы.
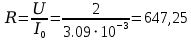 Ом
Ом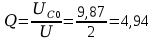
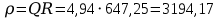 Ом
Ом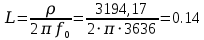 Гн
Гн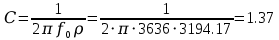 мкФ
мкФ| R,Ом | Q |  , Ом , Ом | C, мкФ | L, Гн |
| 647,25 | 4,94 | 3194,17 | 1,37 | 0,14 |
Амплитудно-частотная характеристика (резонансная кривая) последовательного контура есть зависимость модуля проводимости от частоты:
 ;
;| Измеренные | Вычисл. | |||
| U, В |  , Гц , Гц |  , мА , мА | Y(jw), мСм | |
| 2 | 1834 | 0,41 | 0,000209836 | |
| 2 | 2222 | 0,57 | 0,000299564 | |
| 2 | 2740 | 1 | 0,000514764 | |
| 2 | 3100 | 1,54 | 0,000825975 | |
| 2 | 3279 | 1,98 | 0,001080617 | |
| 2 | 3508 | 2,85 | 0,001456528 | |
| 2 | 3636 | 3,09 | 0,001545 | |
| 2 | 3827 | 2,9 | 0,001378824 | |
| 2 | 4300 | 1,58 | 0,000796086 | |
| 2 | 4651 | 1,2 | 0,000582913 | |
| 2 | 5128 | 0,83 | 0,000428874 | |
| 2 | 5882 | 0,56 | 0,000306965 | |
| 2 | 7143 | 0,42 | 0,000213041 | |
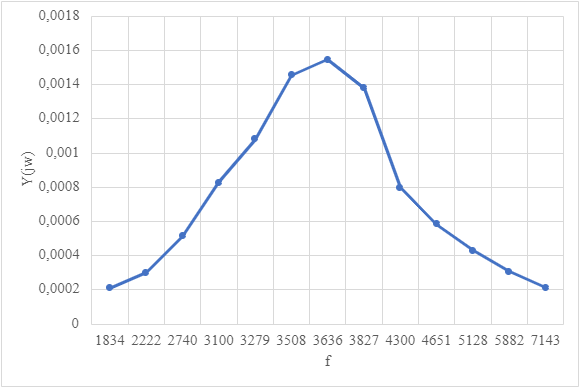
Рисунок 2 – АЧХ контура с большими потерями.
-
Исследование влияния ёмкости на характеристики контура.
| при резонансе таб №5 | |||
| U, В |  , мА , мА |  , Гц , Гц |  , В , В |
| 2 | 3,43 | 1942 | 6,14 |
Расчётные формулы.
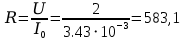 Ом
Ом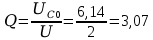 ;
;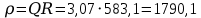 Ом
Ом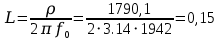 Гн
Гн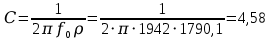 мкФ
мкФ| R, Ом | Q |  , Ом , Ом | C, мкФ | L, Гн |
| 583,1 | 3,07 | 1790,1 | 4,58 | 0,15 |
Амплитудно-частотная характеристика (резонансная кривая) последовательного контура есть зависимость модуля проводимости от частоты:

| таблица №6 | Вычисл. | ||
| U, В |  , Гц , Гц |  , мА , мА | Y(jw), мСм |
| 2 | 926 | 0,67 | 0,000337995 |
| 2 | 1163 | 0,98 | 0,000499049 |
| 2 | 1563 | 1,96 | 0,001023966 |
| 2 | 1786 | 2,88 | 0,001524832 |
| 2 | 1887 | 3,32 | 0,001688916 |
| 2 | 1942 | 3,43 | 0,001715 |
| 2 | 2000 | 3,4 | 0,001687662 |
| 2 | 2247 | 2,8 | 0,001275467 |
| 2 | 2454 | 2,17 | 0,000973701 |
| 2 | 2857 | 1,48 | 0,000652729 |
| 2 | 3508 | 0,93 | 0,00043156 |
| 2 | 3921 | 0,71 | 0,000358512 |